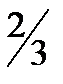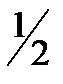Глава v. введение в математический анализ
Лекция №12
ГЛАВА V. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
§ 1. Понятие функции. Способы задания функции. Обратная функция
I. Определение.Пусть даны два непустых множества D и E.
| x |
| D |
| f |
| y |
| E |
def.Если каждому элементу 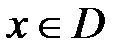 по определенному правилу (закону) f ставится в соответствие единственный элемент
по определенному правилу (закону) f ставится в соответствие единственный элемент 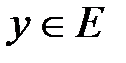 , то говорят, что на множестве D задана функция
, то говорят, что на множестве D задана функция 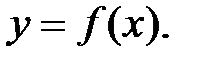
Если D и E – числовые множества 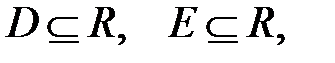
 то
то 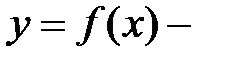 числовая функция.
числовая функция.
Принята следующая терминология:
x – независимая переменная или аргумент;
y – зависимая переменная;
D – область определения функции;
Е – множество значений функции.
Если каждому элементу 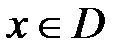 соответствует не одно, а несколько значений
соответствует не одно, а несколько значений 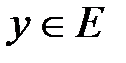 , то получим многозначную функцию (не рассматриваем).
, то получим многозначную функцию (не рассматриваем).
Под функцией будем понимать однозначную числовую функцию.
При конкретном значении аргумента 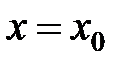 получим частное значение функции
получим частное значение функции 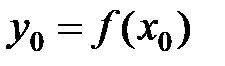 или
или 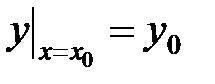 .
.
II. Способы задания функции
- Аналитический. Явное и неявное задание функции
Функция задается аналитическим выражением, т.е. формулой.
Пример 1.1. а) 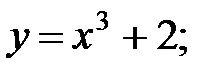 б)
б) 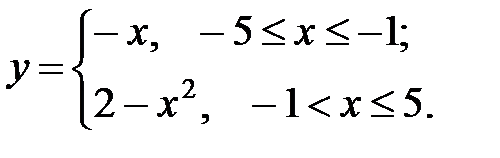
Нельзя отождествлять функцию и формулу: с помощью одной формулы можно задать различные функции (указывая различные области определения), и наоборот, одна функция может быть задана несколькими формулами.
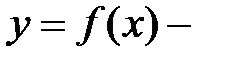 явное задание функции.
явное задание функции.
Пример1.2. 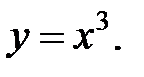
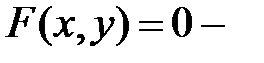 неявное задание функции.
неявное задание функции.
Пример 1.3. а) 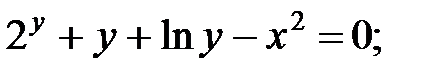
б) 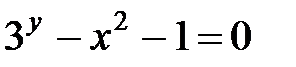 (здесь можно перейти к явному).
(здесь можно перейти к явному).
Преимущества: удобно изучать свойства.Недостатки: малая наглядность.
- Табличный
В таблице указывается в определенном порядке значения аргумента и соответствующие значения функции.
| x | x1 | x2 | … | xn |
| y | y1 | y2 | … | yn |
Пример1.4. Таблицы тригонометрических функций.
Преимущества: Без вычислений находятся соответствующие значения функции.
Недостатки:не можем получить значенийy, неуказанных в таблице.
- Графический
Функция представляется графиком.
Пример1.5. Графики, полученные с помощью самопишущих приборов, например, электрокардиограмма (кривая изменения электрических импульсов сердечной мышцы, вычерчиваемая электрокардиографом); барограммы (кривые зависимости между давлением и временем в метеорологии).
Преимущества: наглядность.
Недостатки: неточность, неудобен при применении математического аппарата.
- Программный
Функция задается с помощью указания программы на одном из машинных языков.
III. Обратная функция
Функция 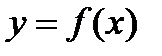 является отображением
является отображением 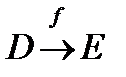 .
.
Рассмотрим взаимнооднозначное отображение (взаимно однозначную функцию).
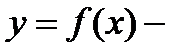 взаимно однозначная функция.
взаимно однозначная функция. 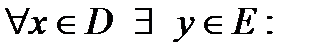
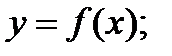
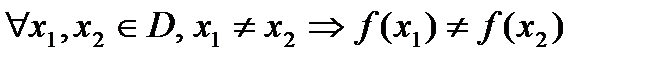
| x |
| y |
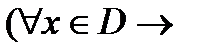 ед.
ед. 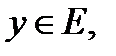 и обратно,
и обратно, 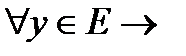 ед.
ед. 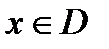 ).
).Пример 1.6.
а) 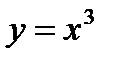 - взаимно однозначная функция
- взаимно однозначная функция
(отображение)
| x |
| y |
б) 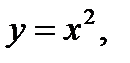 не является взаимно однозначной.
не является взаимно однозначной.
Пусть 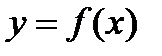 (
( 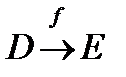 ) – взаимно однозначное отображение. Значит,
) – взаимно однозначное отображение. Значит, 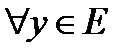 ставится в соответствие ед.
ставится в соответствие ед. 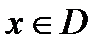 . Тогда говорят, что на множестве Е определена функция, обратная функции
. Тогда говорят, что на множестве Е определена функция, обратная функции 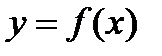 , которая обозначается
, которая обозначается 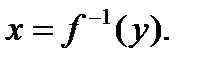
Теорема. Если 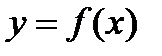 монотонная функция (возрастает или убывает), то существует обратная функция
монотонная функция (возрастает или убывает), то существует обратная функция 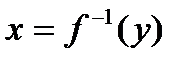 . При этом, если f – возрастающая, то f-1 – возрастающая; если f – убывающая, то и f--1 – убывающая.
. При этом, если f – возрастающая, то f-1 – возрастающая; если f – убывающая, то и f--1 – убывающая.
Пример 2.1.
| 1) | 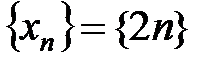 | 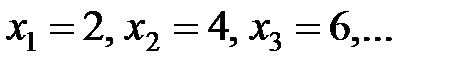 |
| ||||||||||
| 2) | 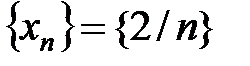 | 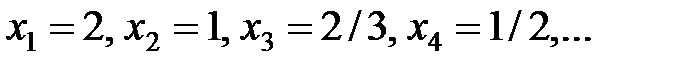 |
| ||||||||||
| 3) | 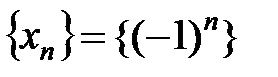 | 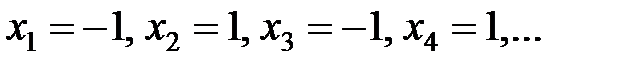 |
| ||||||||||
| 4) | 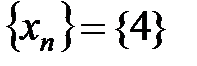 | 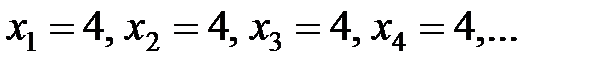 |
I. Определение предела
Рассмотрим упорядоченную переменную, значения которой образуют числовую последовательность 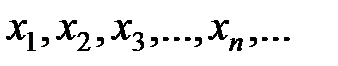
Пример3.1. 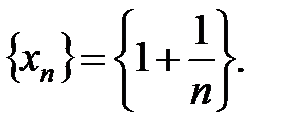
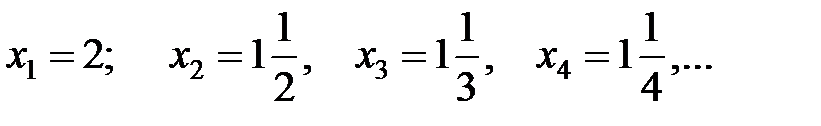
| x |
| 2\4 |
| x3 |
| 1\4 |
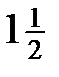 2\4 2\4 |
| x1 |
| x2 |
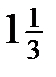 2\4 2\4 |
Значения переменной приближаются к 1, сгущаются около 1 (но никогда 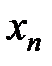 не примет значение, равное 1).
не примет значение, равное 1).
def. Число а называется пределом переменной 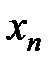 (пределом числовой последовательности), если для любого сколь угодно малого положительного числа
(пределом числовой последовательности), если для любого сколь угодно малого положительного числа 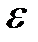 найдется такой номер N, зависящий от
найдется такой номер N, зависящий от 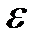 , что для всех значений
, что для всех значений 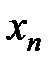 , у которых n>N, будет выполняться неравенство
, у которых n>N, будет выполняться неравенство 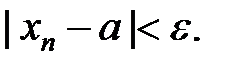
Обозначают: 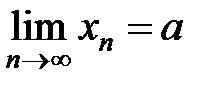 или
или 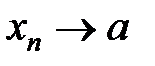 при
при 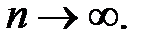
Определение предела на языке символов:
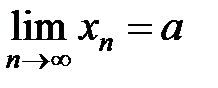
Ограниченная переменная
def.Переменная 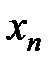 называется ограниченной, если все ее значения по абсолютной величине не превосходят некоторого положительного числа М, т.е.
называется ограниченной, если все ее значения по абсолютной величине не превосходят некоторого положительного числа М, т.е. 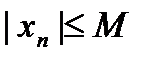 для
для 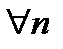 .
.
Теорема. Если переменная имеет конечный предел, то она ограниченная.
Замечание. Обратная теорема не верна.
Например, 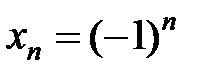 - ограниченная, т.к.
- ограниченная, т.к. 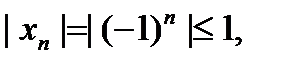 но предела не имеет.
но предела не имеет.
Бесконечно малые величины
I. Определение
def 1.Переменная величина 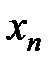 называется бесконечно малой, если ее предел равен 0, т.е.
называется бесконечно малой, если ее предел равен 0, т.е. 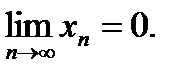
def 2. Переменная величина 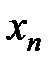 называется бесконечно малой, если для любого сколь угодно малого положительного числа ε найдется такой номер
называется бесконечно малой, если для любого сколь угодно малого положительного числа ε найдется такой номер 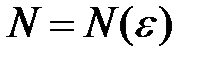 , что для всех значений
, что для всех значений 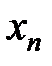 , у которых номер
, у которых номер 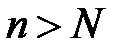 , будет выполняться
, будет выполняться 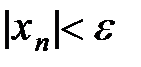
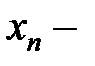 бесконечно малая
бесконечно малая 
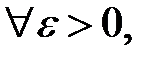
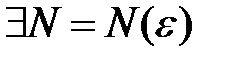 ,
, 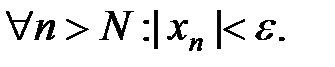
Бесконечно малые (б. м.) величины обозначают: 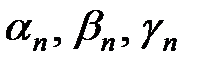 .
.
Пример 5.1.а) 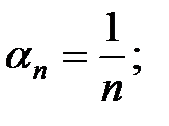 б)
б) 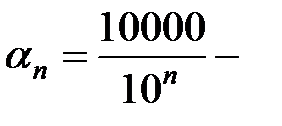 бесконечно малые;
бесконечно малые;
в) 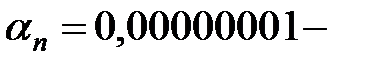 малая величина, но не является беск-но малой, т.к. постоянная.
малая величина, но не является беск-но малой, т.к. постоянная.
Термин «бесконечно малая» не сосем удачный, т.к. величина в процессе изменения становится малой.Единственное число 0 является бесконечно малой.
Пример 6.1.
1) 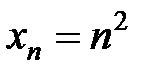 ;2)
;2) 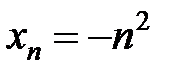 ;3)
;3) 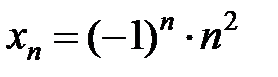 ;
;
4) 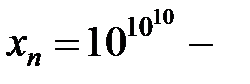 колоссальная величина, но постоянна, не стремится к
колоссальная величина, но постоянна, не стремится к 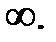
Термин « 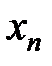 стремится к бесконечности» неточен:
стремится к бесконечности» неточен: 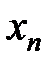 никуда не стремится, ни к какому числу, а изменяется так, что перерастает любое положительное число.
никуда не стремится, ни к какому числу, а изменяется так, что перерастает любое положительное число.
Предел функции
Первый замечательный предел
Функция 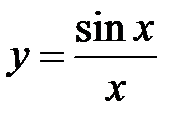 не определена при
не определена при 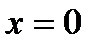 .
.
Рассмотрим 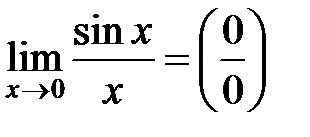 и докажем, что
и докажем, что 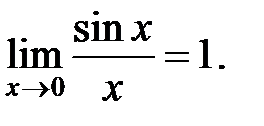
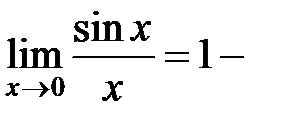 первый замечательный предел.
первый замечательный предел.
Доказательство:
Пример 12.1. 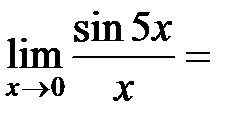
Пример 12.2. 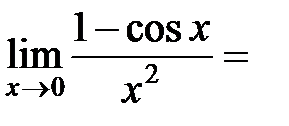
Второй замечательный предел
Рассмотрим переменную 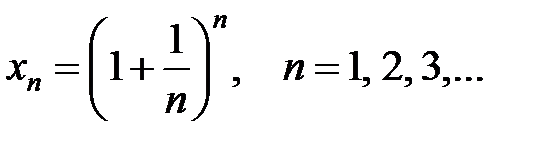
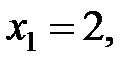
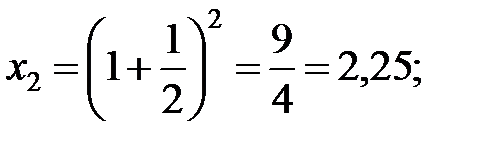
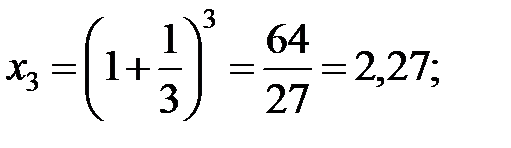
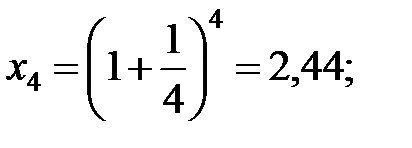
…………………….
Значения 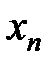 возрастают. Можно доказать, что
возрастают. Можно доказать, что 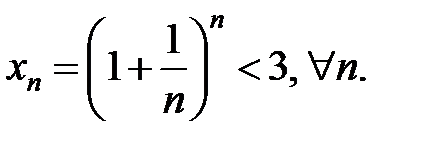
Переменная 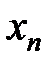 возрастает и ограничена сверху. По 1-му признаку существования переменной существует предел
возрастает и ограничена сверху. По 1-му признаку существования переменной существует предел 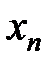 , а именно
, а именно
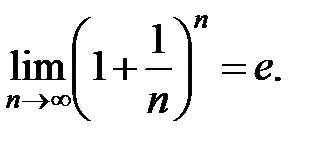
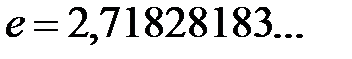
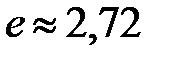 .
.
Логарифмы по основанию е называются натуральными и обозначаются 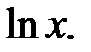
Докажем, что 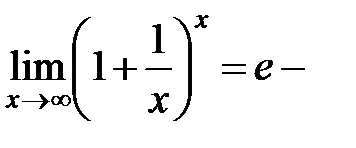 второй замечательный предел.
второй замечательный предел.
Неопределенность вида 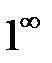 .
.
Доказательство.
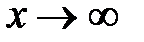 и принимает целые и дробные, положит-ые и отрицат-ые значения.
и принимает целые и дробные, положит-ые и отрицат-ые значения.
Рассмотрим случай, когда 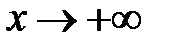 . Для любого положительного числа имеет место неравенство
. Для любого положительного числа имеет место неравенство 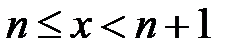 (*) (можно считать, что
(*) (можно считать, что 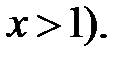
Перейдем к обратным величинам
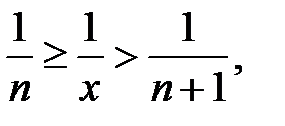 прибавим по 1,
прибавим по 1,
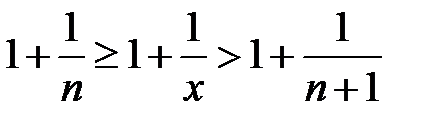 или
или 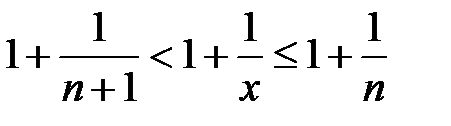 .
.
Возведем в степени с показателями из (*). Неравенство усилится
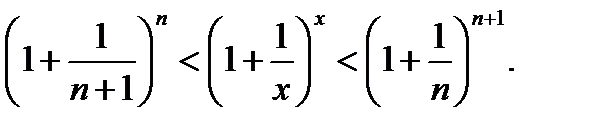
Найдем пределы крайних членов неравенства ( 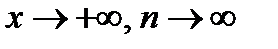 ).
).
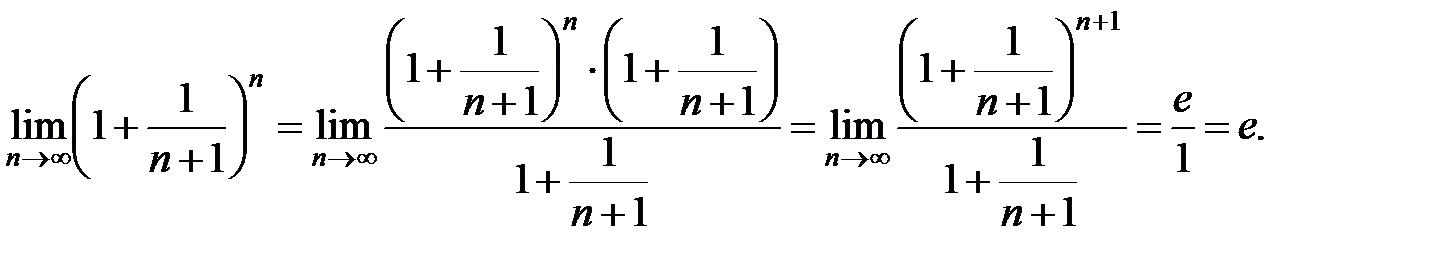
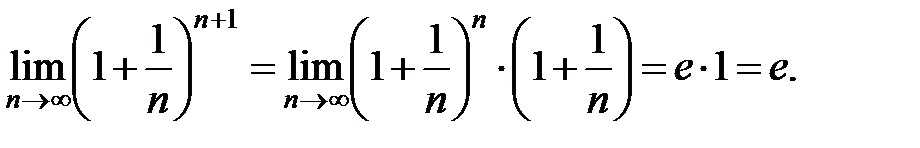
По теореме о сжатой переменной 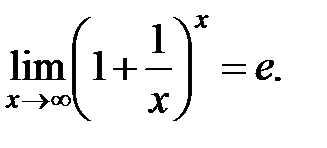
Можно доказать, что 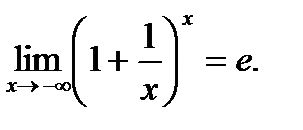
Таким образом, 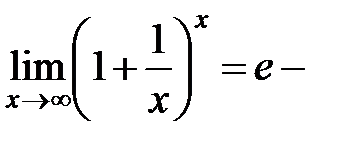 второй замечательный предел.
второй замечательный предел.
Положим 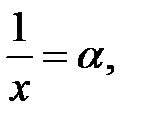 тогда
тогда 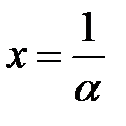 . Если
. Если 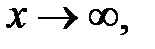 то
то 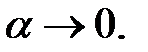
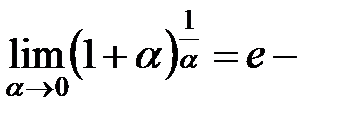 другая форма второго замечательного предела.
другая форма второго замечательного предела.
Пример 13.1. 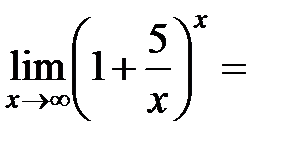
Пример 13.2. 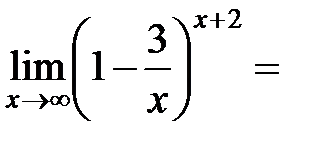
Пример 13.3. 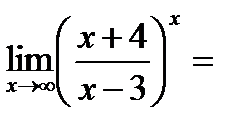
Таблица эквивалентных бесконечно малых
1. 
2. 
3. 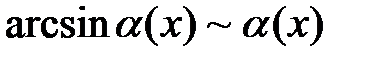
4. 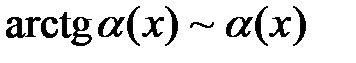 где
где 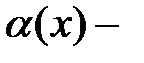 б. м. при
б. м. при 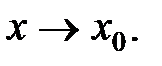
5. 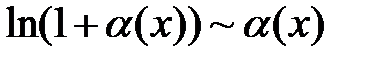
6. 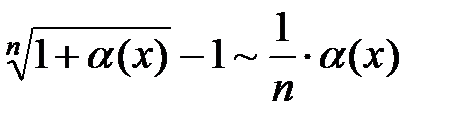
7. 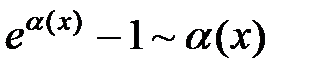
Свойства
1. Предел отношения двух б. м. не изменится, если каждую или только одну заменить эквивалентной бесконечно малой.
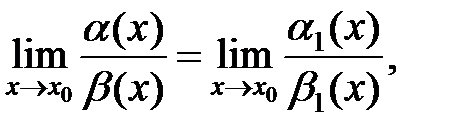 где
где 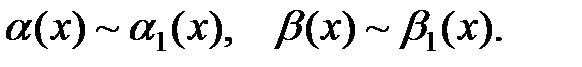
2. Если 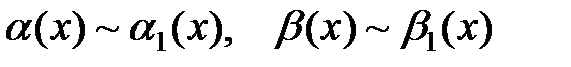 , то
, то 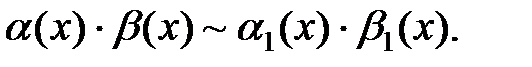 .
.
3. Алгебраическая сумм бесконечно малых различных порядков эквивалентна слагаемому более низкого порядка малости.
Пример. 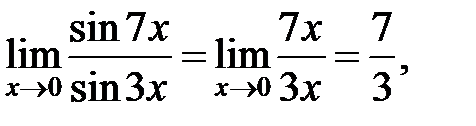 т. к.
т. к. 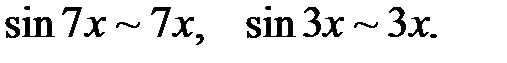
Лекция №12
ГЛАВА V. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
§ 1. Понятие функции. Способы задания функции. Обратная функция
I. Определение.Пусть даны два непустых множества D и E.
| x |
| D |
| f |
| y |
| E |
def.Если каждому элементу  по определенному правилу (закону) f ставится в соответствие единственный элемент
по определенному правилу (закону) f ставится в соответствие единственный элемент 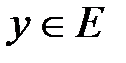 , то говорят, что на множестве D задана функция
, то говорят, что на множестве D задана функция 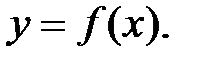
Если D и E – числовые множества 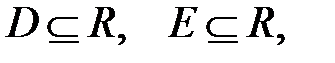
 то
то 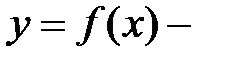 числовая функция.
числовая функция.
Принята следующая терминология:
x – независимая переменная или аргумент;
y – зависимая переменная;
D – область определения функции;
Е – множество значений функции.
Если каждому элементу 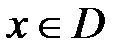 соответствует не одно, а несколько значений
соответствует не одно, а несколько значений 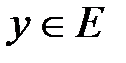 , то получим многозначную функцию (не рассматриваем).
, то получим многозначную функцию (не рассматриваем).
Под функцией будем понимать однозначную числовую функцию.
При конкретном значении аргумента 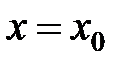 получим частное значение функции
получим частное значение функции 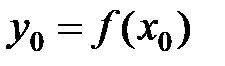 или
или 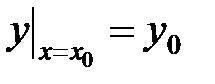 .
.
II. Способы задания функции
- Аналитический. Явное и неявное задание функции
Функция задается аналитическим выражением, т.е. формулой.
Пример 1.1. а) 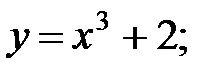 б)
б) 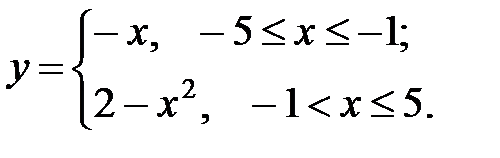
Нельзя отождествлять функцию и формулу: с помощью одной формулы можно задать различные функции (указывая различные области определения), и наоборот, одна функция может быть задана несколькими формулами.
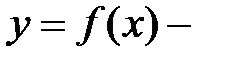 явное задание функции.
явное задание функции.
Пример1.2. 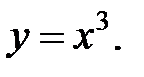
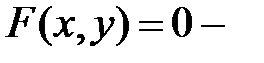 неявное задание функции.
неявное задание функции.
Пример 1.3. а) 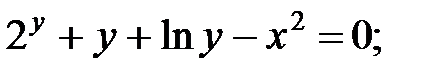
б) 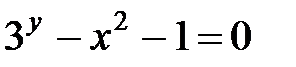 (здесь можно перейти к явному).
(здесь можно перейти к явному).
Преимущества: удобно изучать свойства.Недостатки: малая наглядность.
- Табличный
В таблице указывается в определенном порядке значения аргумента и соответствующие значения функции.
| x | x1 | x2 | … | xn |
| y | y1 | y2 | … | yn |
Пример1.4. Таблицы тригонометрических функций.
Преимущества: Без вычислений находятся соответствующие значения функции.
Недостатки:не можем получить значенийy, неуказанных в таблице.
- Графический
Функция представляется графиком.
Пример1.5. Графики, полученные с помощью самопишущих приборов, например, электрокардиограмма (кривая изменения электрических импульсов сердечной мышцы, вычерчиваемая электрокардиографом); барограммы (кривые зависимости между давлением и временем в метеорологии).
Преимущества: наглядность.
Недостатки: неточность, неудобен при применении математического аппарата.
- Программный
Функция задается с помощью указания программы на одном из машинных языков.
III. Обратная функция
Функция 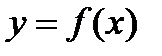 является отображением
является отображением 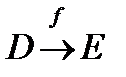 .
.
Рассмотрим взаимнооднозначное отображение (взаимно однозначную функцию).
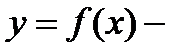 взаимно однозначная функция.
взаимно однозначная функция. 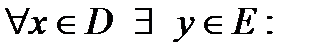
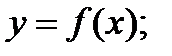
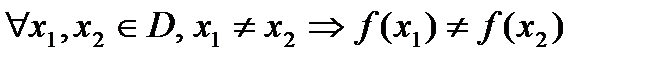
| x |
| y |
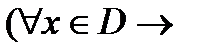 ед.
ед. 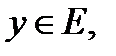 и обратно,
и обратно, 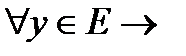 ед.
ед. 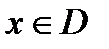 ).
).Пример 1.6.
а) 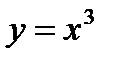 - взаимно однозначная функция
- взаимно однозначная функция
(отображение)
| x |
| y |
б) 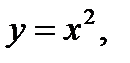 не является взаимно однозначной.
не является взаимно однозначной.
Пусть 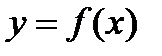 (
( 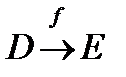 ) – взаимно однозначное отображение. Значит,
) – взаимно однозначное отображение. Значит, 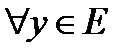 ставится в соответствие ед.
ставится в соответствие ед. 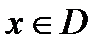 . Тогда говорят, что на множестве Е определена функция, обратная функции
. Тогда говорят, что на множестве Е определена функция, обратная функции 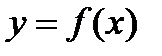 , которая обозначается
, которая обозначается 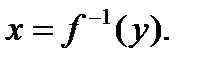
Теорема. Если 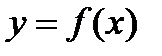 монотонная функция (возрастает или убывает), то существует обратная функция
монотонная функция (возрастает или убывает), то существует обратная функция 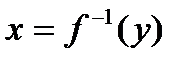 . При этом, если f – возрастающая, то f-1 – возрастающая; если f – убывающая, то и f--1 – убывающая.
. При этом, если f – возрастающая, то f-1 – возрастающая; если f – убывающая, то и f--1 – убывающая.