Глава 1. элементы линейной алгебры
I. Уравнение поверхности.
Уравнение F(x, y) = 0 определяет на плоскости некоторую линию, т. е. множество всех точек плоскости Оху, координаты которых х и у удовлетворяют этому уравнению. Подобно этому уравнение
F(x,y,z) = 0, (1) определяет в пространстве Охуz некоторую поверхность, т. е. множество всех точек, координаты которых х, у, z удовлетворяют уравнению F(x, у, z) = 0. Уравнение (1) называется уравнением этой поверхности, а х, у, z — ее текущими координатами. Часто, однако, поверхность задается не уравнением, а как мно- жество всех точек, обладающих тем или иным свойством. В этом случае требуется найти уравнение поверхности, исходя из ее геометрических свойств.
Пример. Найти уравнение сферы радиуса R с центром в точке 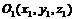
Решение. Согласно определению сферы, расстояние любой ее точки М (х,у, z) от центра 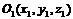 равно радиусу R, т. е.
равно радиусу R, т. е. 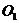 M=R. Но
M=R. Но
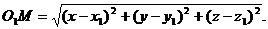
Следовательно, 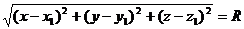 или
или
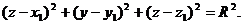 (2)
(2)
Мы получили искомое уравнение сферы, так как ему удовлетворяют координаты любой ее точки и, очевидно, не удовлетворяют координаты точек, не лежащих на данной сфере.
В частности, если центр сферы совпадает с началом координат, то уравнение сферы примет следующий вид:
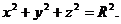 .
.
Раскрыв скобки и перенеся все члены в левую часть уравнения (2), получим
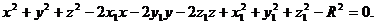
Это уравнение второй степени относительно текущих координат х, у и z. В нем отсутствуют члены с произведениями координат, а коэффициенты при х2 , у2 и z2 равны между собой. Любое уравнение второй степени относительно х, у и z , в котором коэффициенты при х2, y2 и z2 равны между собой, а член с произведением координат отсутствует, есть, вообще говоря, уравнение сферы. Точнее, такое уравнение с помощью выделения полных квадратов всегда может быть приведено к виду:
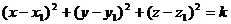 . (3)
. (3)
Если при этом 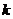 >0, то уравнение (3) является уравнением сферы с центром в точке
>0, то уравнение (3) является уравнением сферы с центром в точке 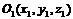 и радиусом R =
и радиусом R = 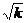 . При k = 0 уравнению удовлетворяют координаты лишь одной точки
. При k = 0 уравнению удовлетворяют координаты лишь одной точки 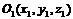 . Если же
. Если же 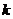 <0, то уравнение не определяет никакой поверхности.
<0, то уравнение не определяет никакой поверхности.
Пример.Доказать, что уравнение
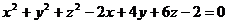
является уравнением сферы, и найти центр и радиус этой сферы.
Решение. Преобразуя левую часть данного уравнения, полу- чим
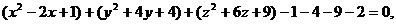 или
или 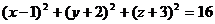 .
.
Мы получили уравнение сферы с центром в точке О(1; - 2; - 3) и радиусом R = 4.
Цилиндрические поверхности.
Поверхность, составленная из всех прямых, пересекающих данную линию L и параллельных данной прямой l, называется цилиндрической поверхностью. При этом линия L называется направляющей цилиндрической поверхности, а каждая из прямых, составляющих эту поверхность и параллельных прямой  - образующей. В дальнейшем мы будем рассматривать только такие цилиндрические поверхности, направляющие которых лежат в одной из координатных плоскостей, а образующие параллельны координатной оси, перпендикулярной этой плоскости. Рассмотрим в плоскости Оху некоторую линию L, имеющую в системе координат Оху уравнение:
- образующей. В дальнейшем мы будем рассматривать только такие цилиндрические поверхности, направляющие которых лежат в одной из координатных плоскостей, а образующие параллельны координатной оси, перпендикулярной этой плоскости. Рассмотрим в плоскости Оху некоторую линию L, имеющую в системе координат Оху уравнение:
F(x,y)=0, (4)
Построим цилиндрическую поверхность с образующими, параллельными оси Oz, и направляющей L . Покажем, что уравнение этой поверхности есть уравнение (4), если его отнести к системе координат в пространстве Oxyz. Пусть М (х; у; z) -любая фиксированная точка построенной цилиндрической поверхности. Обозначим через N точку пересечения направляющей L и образующей, проходящей через точку М. Точка N, очевидно, есть проекция точки М на плоскость Оху. Поэтому точки М и N имеют одну и ту же абсциссу х и одну и ту же ординату у. Но точка N лежит на кривой L, и ее координаты х и у удовлетворяют уравнению (4) этой кривой. Следовательно, этому уравнению удовлетворяют и координаты точки М (х; у; z), так как оно не содержит z. Таким образом, координаты любой точки М (х; у;z) данной цилиндрической поверхности удовлетворяют уравнению (4). Координаты же точек, не лежащих на этой поверхности, уравнению (4) не удовлетворяют, так как эти точки проектируются на плоскость Оху вне кривой L. Таким образом, не содержащее z уравнение F(x, y) = 0, если его отнести к системе координат в пространстве Oxyz, является уравнением цилиндрической поверхности с образующими, параллельными оси Oz, и направляющей L, которая в плоскости Оху задается тем же уравнением F (х, у) = 0.
В пространстве Оху направляющая L определяется системой двух уравнений:
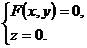 (5)
(5)
Рис.1.
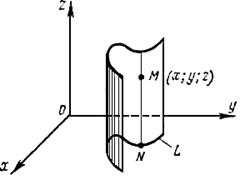
Алогично можно показать, что уравнение F (x, z) = 0, не содержащее у, и уравнение F (у, z) = 0, не содержащее х, определяют в пространстве Oxyz цилиндрические поверхности с образующими, параллельными соответственно осям Оу и Ох.
Рассмотрим примеры цилиндрических поверхностей.
1. Поверхность, определяемая уравнением
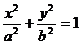 . (6)
. (6)
является цилиндрической и называется эллиптическим цилиндром (рис. 2). Ее образующие параллельны оси Oz, а направляющей является эллипс с полуосями а и Ь, лежащий в плоскости Оху. В частности, если a = b, то направляющей является окружность, а поверхность является прямым круговым цилиндром. Его уравнение
х2 + у2 = а2.
2.Цилиндрическая поверхность, определяемая уравнением
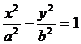 . (7)
. (7)
называется гиперболическим цилиндром (рис. 3). Образующие этой поверхности параллельны оси Оу, а направляющей служит расположенная в плоскости Охz гипербола с действительной полуосью a и мнимой полуосью b.
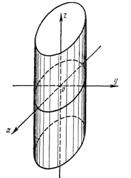
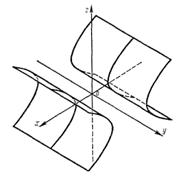
Рис.2 Рис.3
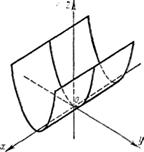 Рис.4.
Рис.4.
3. Цилиндрическая поверхность, определяемая уравнением
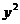 = 2pz, (8)
= 2pz, (8)
Называется параболическим цилиндром (рис.4). Ее направляющей является парабола, лежащая в плоскости Oyz, а образующие параллельны оси Ох.
Замечание. Как известно, прямая в пространстве может быть задана уравнениями различных пар плоскостей, пересекающихся по этой прямой. Подобно этому кривая в пространстве может быть задана с помощью уравнений различных поверхностей, пересекающихся по этой кривой. Например, окружность С, получающаяся в сечении плоскостью z = 3 сферы 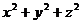 = 25 , может быть задана системой уравнений
= 25 , может быть задана системой уравнений
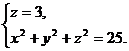 (9)
(9)
С другой стороны, эта окружность может быть получена как линия пересечения плоскости z = 3 и прямого кругового цилиндра 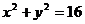 .
.
В дальнейшем, исследуя форму той или иной поверхности с помощью сечений, параллельных координатным плоскостям, мы не разбудем пользоваться цилиндрическими поверхностями, проектирующими эти сечения на координатные плоскости. Это позволит так же, как в рассмотренном примере, судить о размерах и форме указанных сечений, а тем самым и о форме исследуемых поверхностей.
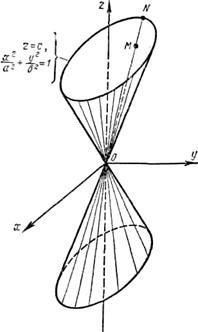
Конические поверхности.
Поверхность, составленная из всех прямых, пересекающих данную линию L и проходящих через данную точку Р, называется конической поверхностью. При этом линия L называется направляющей конической поверхности, точка Р - ее вершиной, а каждая из прямых, составляющих коническую поверхность, образующей.
В качестве примера рассмотрим коническую поверхность с вершиной в начале координат, для которой направляющей является эллипс:
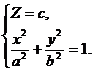 (10)
(10)
с полуосями а и b, лежащий в плоскости Z = c. Эта поверхность называется конусом второго порядка. Выведем ее уравнение.
Рассмотрим произвольно выбранную точку М (х; у; z ) конической поверхности и проведем через нее образующую ОМ, пересекающуюся с направляющей в точке N (X; Y; с) (рис. 5). Составим уравнение прямой ОМ, проходящей через точки 0 (0; 0; 0) и N (X; У; с)
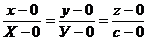 или
или 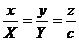 .
.
Отсюда X = cx/z; Y = cy/z. Подставив эти выражения во второе из уравнений эллипса (11), получим 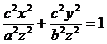 , или, после преобразования,
, или, после преобразования, 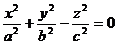 .
.
Мы получили уравнение конуса второго порядка. В частности, если а = b, то направляющей является окружность
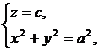
а поверхность является прямым круговым конусом. Его уравнение
 |
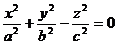 . (11)
. (11)
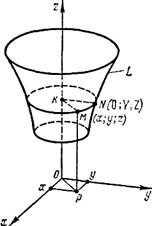
Рис6 Рис. 5
Поверхность вращения.
Пусть линия L, лежащая в плоскости Oyz, задана уравнениями
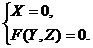 (12)
(12)
Рассмотрим поверхность, образованную вращением этой линии относительно оси Оz (рис. 6). ( Текущие координаты линии L мы обозначаем большими буквами X, Y в Z, чтобы отличить их от текущих координат х, у, z поверхности вращения.)
Эта поверхность называется поверхностью вращения. Найдем ее уравнение. Пусть М (х; у; z) - произвольно выбранная точка поверхности вращения. Проведем через точку М плоскость, перпендикулярную оси Oz, и обозначим точки пересечения этой плоскости с осью Oz и кривой L соответственно через К и N. Отрезки КМ и KN являются радиусами одной и той же окружности. Поэтому КМ = KN. Но длина отрезка KN равна абсолютной величине ординаты Y точки N, т. е. KN = |Y|, a KM = OP = 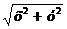 . Следовательно,
. Следовательно,
| Y |= 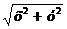 или Y =
или Y = 
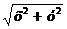 . Кроме того, аппликата Z точки N, очевидно, равна аппликате z точки М.
. Кроме того, аппликата Z точки N, очевидно, равна аппликате z точки М.
Так как точка N лежит на линии L, заданной уравнениями (12), то координаты Y и Z точки N удовлетворяют второму из этих уравнений. Подставляя в него вместо Y и Z, соответственно, равные им величины 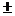
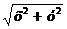 и z, получим уравнение:
и z, получим уравнение:
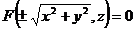 , (13)
, (13)
которому удовлетворяют координаты любой точки М (х; у; z) поверхности вращения. Можно показать, что координаты точек, не лежащих на этой поверхности, уравнению (13) не удовлетворяют. Таким образом, уравнение (13) является уравнением поверхности вращения относительно оси Оz линии L, определяемой уравнениями (12). Уравнение (13) получается из второго уравнения системы (12) заменой в нем координат Y и Z координатами х, у и z по формулам:
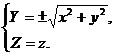 (14)
(14)
Замечание. Мы считали, что кривая L задана в плоскости Oyz и вращается относительно оси Oz. Однако кривая L может быть задана и в другой координатной плоскости и может вращаться относительно другой координатной оси. Формулы, подобные формулам (12), (13) и (14), легко составить.
Пример. Найти уравнение поверхности вращения эллипса
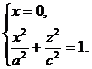
относительно оси Оz.
Решение. Записав уравнение эллипса в виде
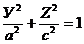
и заменяя в нем по формулам (14) Y и Z текущими координатами х, у и z поверхности вращения, получим искомое уравнение 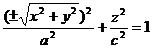 , или
, или
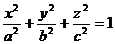 .
.
Полученная поверхность называется эллипсоидом вращения.


 5. Эллипсоид.
5. Эллипсоид.
Поверхность, определяемая уравнением
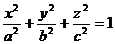 . (15)
. (15)
Называется эллипсоидом. Числа а, b и с называются полуосями эллипсоида. Так как в уравнение (15) текущие координаты входят в четных степенях, то эллипсоид симметричен относительно координатных плоскостей. Чтобы установить форму эллипсоида, будем пересекать его плоскостями, параллельными координатным плоскостям. Покажем, что если пересечь эллипсоид плоскостью z = h (| h | < с), то в сечении получится эллипс L. В самом деле, исключая из уравнений
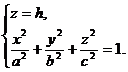
аппликату z, получим уравнение цилиндрической поверхности, проектирующей сечение L на плоскость Оху:
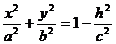 , или
, или
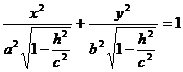
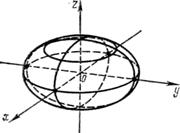 |
Рис..7.
Из этого уравнения видно, что кривая L есть эллипс с полуосями
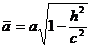 ,
, 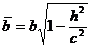 . (16)
. (16)
Из формул (16) видно, что с возрастанием |h| полуоси эллипса а и b уменьшаются. При |h|=c имеем 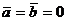 , и сечение вырождается в точку. При |h|>с эллипсоид с плоскостью z = h, очевидно, не пересекается. Аналогично можно показать, что при пересечении эллипсоида плоскостями х = h (| h | < а и y = h (| h | < b ) также получатся эллипсы. Эллипсоид имеет вид, изображенный на рис. 7. В частном случае при а = b получаем эллипсоид вращения
, и сечение вырождается в точку. При |h|>с эллипсоид с плоскостью z = h, очевидно, не пересекается. Аналогично можно показать, что при пересечении эллипсоида плоскостями х = h (| h | < а и y = h (| h | < b ) также получатся эллипсы. Эллипсоид имеет вид, изображенный на рис. 7. В частном случае при а = b получаем эллипсоид вращения
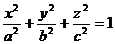 . (17)
. (17)
Если все три полуоси равны между собой, с = b = а, то получится сфера 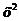 + y2 + z2 = а2.
+ y2 + z2 = а2.
Гиперболоиды.
Поверхность, определяемая уравнением
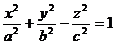 . (18)
. (18)
называется однополостным гиперболоидом. Эта поверхность имеет три плоскости симметрии - координатные плоскости, так как текущие координаты х, у и z входят в уравнение (18) в четных степенях. Пересекая однополостный гиперболоид плоскостью у = 0, получим лежащую в плоскости Oxz гиперболу ABCD (рис. 8)
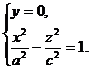
Аналогично, в сечении однополостного гиперболоида плоскостью х = 0 получится гипербола EFGH
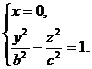
лежащая в плоскости Oyz.
При пересечении однополостного гиперболоида плоскостью z = h получится эллипс BFCG, уравнения которого имеют вид: 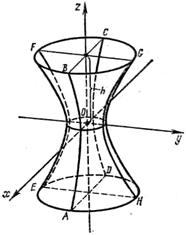
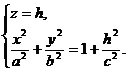 или
или
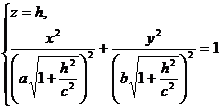 .
.
Рис. 8
| |
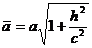 и
и 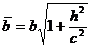 возрастают с возрастанием абсолютной величины h . При h = 0 получится эллипс, лежащий в плоскости Оху и имеющий наименьшие полуоси а и b.
возрастают с возрастанием абсолютной величины h . При h = 0 получится эллипс, лежащий в плоскости Оху и имеющий наименьшие полуоси а и b. При а = b получим однополостный гиперболоид
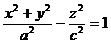 . (19)
. (19)
При пересечении его плоскостями z = h получаются окружности
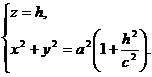
В п. 2 и 3 рассматривались цилиндрические и конические поверхности каждая из которых составлена из прямых. Оказывается, однополостный гиперболоид можно также рассматривать как поверхность, составленную из прямых линий. Рассмотрим прямую, определяемую уравнениями:
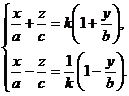 (20)
(20)
в которых а, b и с - полуоси однополостного гиперболоида, а 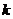 - произвольно выбранное число (
- произвольно выбранное число ( 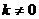 ).
).
Перемножив левые и правые части этих уравнений, получим :
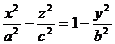 , или
, или 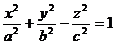 ,
,
т. е. получим уравнение однополостного гиперболоида.
Таким образом, уравнение однополостного гиперболоида является следствием системы уравнений (20). Поэтому координаты любой точки М (х; у; z), удовлетворяющие системе (20), удовлетворяют также и уравнению (18) однополостного гиперболоида. Иными словами, все точки прямой (20) принадлежат гиперболоиду (18). Меняя значения k, мы получим целое семейство прямых, лежащих на поверхности (18). Аналогично можно показать, что однополостному гиперболоиду принадлежат все прямые семейства:
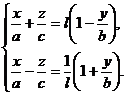 (21)
(21)
Где l — произвольный параметр.
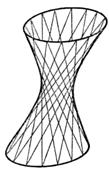
Рис. 9
Можно также показать, что через каждую точку однополостного гиперболоида проходит по одной прямой каждого из указанных семейств. Таким образом, однополостный гиперболоид можно рассматривать как поверхность, составленную из прямых линий (рис. 9). Эти прямые называются прямолинейными образующими однополостного гиперболоида.
Возможность составления поверхности однополостного гиперболоида из прямых линий используется в строительной технике. Так, например, по конструкции, предложенной инженером Шуховым , в Москве была сооружена радиомачта с помощью балок, расположенных по прямолинейным образующим однополостного гиперболоида.
Поверхность, определяемая уравнением
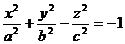 , (22)
, (22)
называется двуполостным гиперболоидом.
Координатные плоскости являются плоскостями симметрии для двуполостного гиперболоида. Пересекая эту поверхность координатными плоскостями Oxz и Оуz, получим соответственно гиперболы
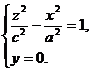 и
и 
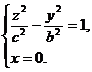
 Рис.10
Рис.10
Если двуполостный гиперболоид пересечь плоскостью
z = h (при | h |>c ), то в сечении получится эллипс
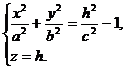
с полуосями
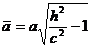 и
и 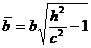 ,
,
возрастающими при возрастании | h |. При | h |<с поверхность (22) с плоскостью z = h, очевидно, не пересекается. Двуполостный гиперболоид состоит из двух отдельных частей (полостей), чем и объясняется его название. При а = b уравнение (22) имеет вид
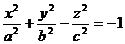 или
или 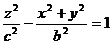 . (23)
. (23)
и является уравнением двуполостного гиперболоида вращения. В сечении последнего с плоскостью z = h (| h |>c) получится окружность
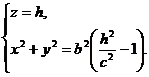 радиуса R=
радиуса R= 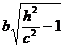 .
.
Параболоиды.
Эллиптическим параболоидом называется поверхность, определяемая уравнением
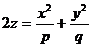 , (24)
, (24)
при условии, что р и q имеют одинаковые знаки. В дальнейшем, для определенности, будем считать, что р>0, q>0.
При пересечении эллиптического параболоида координатными плоскостями Oxz и Oyz получатся, соответственно, параболы
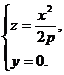 и
и 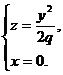
а при пересечении плоскостью z = h (h >0) - эллипс
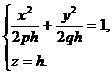
с полуосями 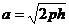 и
и 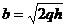 (рис. 11). В случае
(рис. 11). В случае
p = q получим параболоид вращения
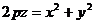 . (25)
. (25)
Поскольку х и у входят в уравнение (24) в четных степенях, эллиптический параболоид имеет две плоскости симметрии: Oxz и Oyz.
Рис.11 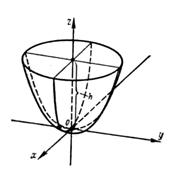
Рис.12. 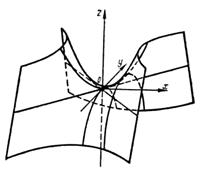
Гиперболическим параболоидом называется поверхность, определяемая уравнением
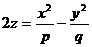 . (26)
. (26)
при условии, что р и q имеют одинаковые знаки. (В дальнейшем, для определенности, будем считать, что р>0, q>0.)
Пересекая эту поверхность плоскостью Oxz, получим параболу
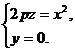 (27)
(27)
(рис.12.)
При пересечении гиперболического параболоида плоскостью x = h получится парабола
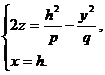 или
или 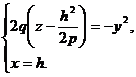
При различных значениях h получится целое семейство парабол, лежащих в плоскостях, параллельных плоскости Oyz и имеющих одинаковый параметр q.
Гиперболический параболоид можно рассматривать как поверхность, описываемую движением любой из этих парабол при условии, что плоскость движущейся параболы остается параллельной плоскости Oyz, ось симметрии параболы остается в плоскости Oxz, а вершина движется по параболе (27). Пересекая гиперболический параболоид плоскостью z = h, получим (при 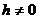 ) гиперболу:
) гиперболу:
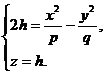 или
или 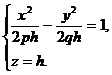
|
На рис. 12 показано расположение этой гиперболы для двух случаев: h >0 и h <0. При h = 0, т. е. при пересечении гиперболического параболоида координатной плоскостью Оху, получится линия, уравнение которой в плоскости Оху имеет вид:
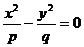 .
.
Последнее уравнение равносильно системе двух уравнений
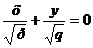 ,
, 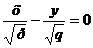 .
.
Это означает, что гиперболический параболоид пересекается с плоскостью Оху по двум прямым :
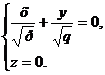 и
и 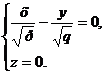
лежащим в плоскости Оху и проходящим через начало координат. Кроме этих двух прямых, существуют и другие прямые, полностью лежащие на гиперболическом параболоиде. Более того, как и в случае однополостного гиперболоида, можно показать, что через каждую точку гиперболического параболоида проходит по одной прямой каждого из двух семейств прямых:
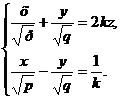 и
и 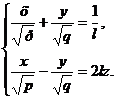
где k и l - произвольные параметры.
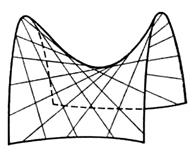
Таким образом, гиперболический параболоид можно рассматривать как поверхность, составленную из прямых линий (Рис. 13).
Замечание. Поверхности, составленные из прямых линий, называются линейчатыми. Таким образом, цилиндрические и конические поверхности, а также однополостный гиперболоид и гиперболический параболоид являются линейчатыми поверхностями.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Беклемешев Д.В. Курс аналитической геометрии и линейной алгебры - М. Наука, 1980.
2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической Геометрии - М. Наука, 1980.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая мате- матика в упражнениях и задачах, 1 ч. - М. Высш. шк., 1986.
4. Изосов А.В., Изосова Л.А. Векторная алгебра и аналити- ческая геометрия - Учебное пособие, Магнитогорск, 2001.
5. Щипачёв В.С. Высшая математика - М., Высш. шк., 1985.
6. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики - М., Высш. шк., 1978.
СОДЕРЖАНИЕ
ГЛАВА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ…………… 3
§ 1. Матрицы и алгебраические действия с ними. ………… 3
§ 2. Определители матриц и их свойства. …………………….. 8
§ 3. Обратная матрица. …………………………………………….. 16
§ 4. Системы линейных алгебраических уравнений. ………… 21
ГЛАВА 2. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. ………….. 46
§ 1. Вектор. Алгебраические действия с векторами. ………. 46
§ 2. Системы координат на прямой, в плоскости и в
пространстве …………………………………………………… 49
§ 3. Нелинейные операции над векторами. ………………….. 57
§ 4. Понятие евклидова пространства. ………………………… 69
ГЛАВА 3. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ. 72
§ 1. Прямая линия на плоскости. …………………………………72
§ 2. Взаимное расположение прямых на плоскости. ……….. 75
§ 3. Плоскость в пространстве. …………………………………... 79
§ 4. Прямая в пространстве. ……………………………………… 83
§ 5. Взаимное расположение прямой и плоскости в
постранстве. ……………………………………………………… 87
§ 6. Линии второго порядка на плоскости. …………………….. 97
§ 7. Полярная система координат. …………………………….... 114
§ 8. Поверхности второго порядка. ……………………………. 122
БИБЛИОГРАФИЧЕСКИЙ СПИСОК …………………………… 141
ГЛАВА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
§ 1. МАТРИЦЫ И АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ С НИМИ.
Определение. Матрицей называется прямоугольная табли –ца состоящая из 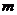 строк и
строк и 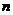 столбцов, заполненная либо числами, либо некоторыми символами, при этом говорят, что она имеет размерность
столбцов, заполненная либо числами, либо некоторыми символами, при этом говорят, что она имеет размерность 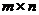 . Общий вид матрицы можем представить следующим образом:
. Общий вид матрицы можем представить следующим образом:

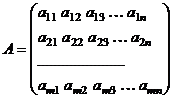 ,
, 
или, в более компактном виде: 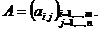
Если 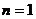 , т.е. матрица размерности
, т.е. матрица размерности 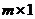 , то матрицу на- зывают вектор – столбцом, если
, то матрицу на- зывают вектор – столбцом, если 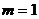 , т.е. матрица размер -ности
, т.е. матрица размер -ности 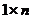 , то её называют вектор – строкой. Матрица, у ко- торой все элементы равны нулю, называется нулевой. Матри -ца, у которой число строк
, то её называют вектор – строкой. Матрица, у ко- торой все элементы равны нулю, называется нулевой. Матри -ца, у которой число строк 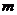 равно числу столбцов
равно числу столбцов 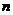 назы – ется квадратной матрицей порядка
назы – ется квадратной матрицей порядка 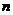 .
.
Элементы 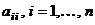 образуют главную диагональ квад- ратной матрицы. Если равны нулю все элементы квадратной матрицы, кроме элементов главной диагонали, которые не все равны нулю, то матрица называется диагональной порядка
образуют главную диагональ квад- ратной матрицы. Если равны нулю все элементы квадратной матрицы, кроме элементов главной диагонали, которые не все равны нулю, то матрица называется диагональной порядка 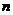 . Если все элементы главной диагонали диагональной матрицы равны между собой, то она называется скалярной. Диагональ- ная матрица, все диагональные элементы которой равны 1, называпется единичной. Если все элементы квадратной матри- цы, расположенные выше (или ниже) главной диагонали равны нулю, то матрица называется треугольной. Приведём приме -ры перечисленных матриц:
. Если все элементы главной диагонали диагональной матрицы равны между собой, то она называется скалярной. Диагональ- ная матрица, все диагональные элементы которой равны 1, называпется единичной. Если все элементы квадратной матри- цы, расположенные выше (или ниже) главной диагонали равны нулю, то матрица называется треугольной. Приведём приме -ры перечисленных матриц:
1. Вектор – столбец размерности 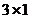 :
:
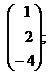
2. Вектор – строка размерности 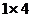 :
: 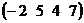 :
:
3. Нулевая матрица размерности 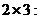
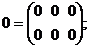
4 Квадратная матрица порядка 3:
5. Диагональная матрица четвёртого порядка:
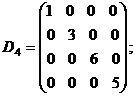
6. Скалярная матрица второго порядка :
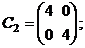
7. Единичная матрица третьего порядка:
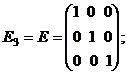
8. Треугольные матрицы:
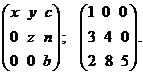
Две матрицы 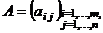 и
и 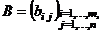 называют- ся равными, если они имеют одинаковые размерности
называют- ся равными, если они имеют одинаковые размерности 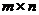 и совпадают элементы с одинаковыми индексами (т.е. совпа- дают элементы, расположенные на одинаковых местах):
и совпадают элементы с одинаковыми индексами (т.е. совпа- дают элементы, расположенные на одинаковых местах):
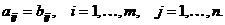
В этом случае пишут 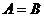 .
.
АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ С МАТРИЦАМИ
1. Умножение матрицы на число.: возможно для матриц лю-
бой размерности. При умножении матрицы на число каждый элемент матрицы умножается на это число, т.е.
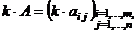 ,
,
Например, если 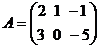 , то
, то 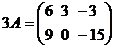 .
.
2. Алгебраическое сложение матриц (т.е. сложение и вычи- тание) можно выполнять только для матриц одинаковой раз –мерности и производится поэлементно, т.е., если даны две матрицы 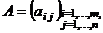 и
и 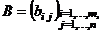 , то
, то
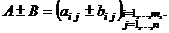
Например, если 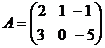 ,
, 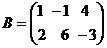 , то
, то
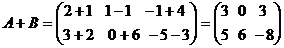 ;
;
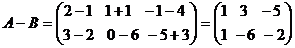 .
.
3. Умножение матриц возможно только в том случае, ес- ли число столбцов первой матрицы равно числу строк вто- рой матрицы. В результате умножения получается матрица, у которой число строк равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы.
Замечание. Согласно этому правилу, умножение матриц возможно далеко не всегда. Кроме того, даже если умножение матриц возможно, нельзя менять их местами при умножении, так как это может привести к совершенно различным резуль- татам.
Таким образом, если 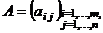 , а
, а 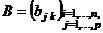 , т.е. в матрице
, т.е. в матрице 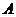
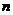 столбцов, а в матрице
столбцов, а в матрице 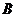
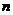 строк, то после умножения получится матрица
строк, то после умножения получится матрица 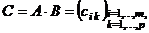 , где элемент
, где элемент 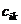 равен сумме произведений соответствующих элементов
равен сумме произведений соответствующих элементов 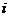 -й строки матрицы
-й строки матрицы 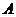 и
и 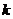 -го столбца матрицы
-го столбца матрицы 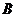 , т.е.
, т.е.
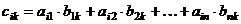 ,
,
где 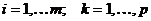 .
.
Чтобы понятнее был способ умножения матриц, рассмотрим следующий пример 1:
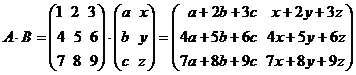 .
.
Ещё один пример 2 умножения числовых матриц:
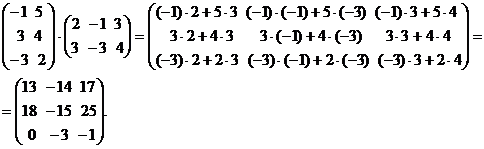
Перемножим эти же матрицы в другом порядке:
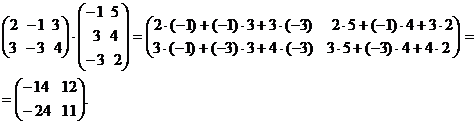 Умножение этих матриц также было возможно, но в резуль- тате умножения получили совершенно другую матрицу, более того, даже матрицу другой размерности.
Умножение этих матриц также было возможно, но в резуль- тате умножения получили совершенно другую матрицу, более того, даже матрицу другой размерности.
Матрицы же, рассмотренные в примере 1, вообще нельзя перемножить в другом порядке, так как у второй матрицы 2 столбца, а у первой матрицы 3 строки и, согласно правилу умножения, умножение таких матриц невозможно. Поэтому ум- ножение матриц антикоммутативно, т.е., в общем случае, 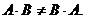
Деление для матриц не определяется, но можно для неко- торых матриц ввести понятие обратной матрицы (только для квадратных невырожденных матриц).
Определение. Матрица 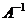 называется обратной к матри- це
называется обратной к матри- це 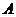 , если выполняется равенство:
, если выполняется равенство:
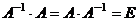 ,
,
где 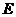 - единичная матрица.
- единичная матрица.
В завершение параграфа отметим следующие свойства алгебраических действий с матрицами.
Пусть 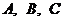 - некоторые матрицы,
- некоторые матрицы, 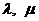 - числа. Тогда можно легко убедиться в справедливости следующих равенств:
- числа. Тогда можно легко убедиться в справедливости следующих равенств:
1) 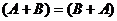 (коммутативность сложения);
(коммутативность сложения);
2) 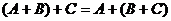 (ассоциативность сложения);
(ассоциативность сложения);
3) Для любой матрицы 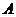 размерности
размерности 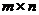 существует нулевая матрица
существует нулевая матрица 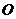 той же размерности, такая что выполнено:
той же размерности, такая что выполнено:
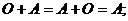
4) Для любой матрицы 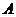 существует противоположная мат- рица
существует противоположная мат- рица 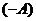 , такая что
, такая что 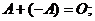
5) 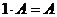 для любой матрицы
для любой матрицы 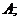
6) 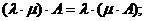
7) 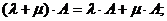
8) 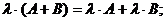
9) 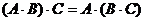 , если умножение возможно (ассо -циативность умножения);
, если умножение возможно (ассо -циативность умножения);
10) 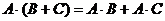 , если все эти операции воз -можны (дистрибутивность умножения);
, если все эти операции воз -можны (дистрибутивность умножения);
11) 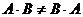 (антикоммутативность);
(антикоммутативность);
12) Для любой невырожденной квадратной матрицы су -ществует обратная матрица, такая что 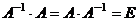 .
.
§ 2 ОПРЕДЕЛИТЕЛИ МАТРИЦ И ИХ СВОЙСТВА
Любой квадратной матрице 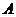 по некоторому правилу можно поставить в соответствие некоторое число, которое называется её определителем и обозначается либо
по некоторому правилу можно поставить в соответствие некоторое число, которое называется её определителем и обозначается либо 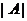 , ли- бо
, ли- бо 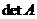 , либо просто
, либо просто 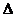 .
.
Для матрицы второго порядка
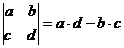 .
.
Например:
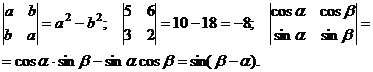
Для вычисления определителей третьего порядка удобно воспользоваться, так называемым правилом треугольников:
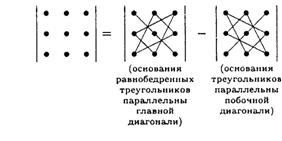
Согласно этому правилу, определитель матрицы третьего порядка вычисляется по формуле:
<