Тема 1: Спецификация эконометрической модели
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 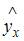 . Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для
. Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для 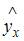 , но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.
, но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.
2. Для регрессионной модели вида 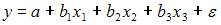 необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
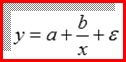
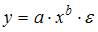
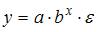
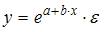
Решение:
Из приведенных функций только в функции 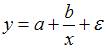 параметры имеют степень 1, а объясняющая переменная х имеет степень, отличную от 1.
параметры имеют степень 1, а объясняющая переменная х имеет степень, отличную от 1.
4. В модели вида 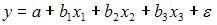 количество объясняющих переменных равно …
количество объясняющих переменных равно …
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 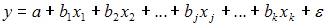 , где y – зависимая переменная; xj – объясняющая независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии);
, где y – зависимая переменная; xj – объясняющая независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии); 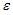 – случайные факторы. Независимые переменные xj называются также факторами, объясняющими переменными. На количество объясняющих переменных в линейном уравнении указывает также количество коэффициентов регрессии bj. Поэтому количество объясняющих переменных в модели равно 3.
– случайные факторы. Независимые переменные xj называются также факторами, объясняющими переменными. На количество объясняющих переменных в линейном уравнении указывает также количество коэффициентов регрессии bj. Поэтому количество объясняющих переменных в модели равно 3.
5. При идентификации модели множественной регрессии 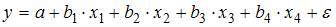 количество оцениваемых параметров равно …
количество оцениваемых параметров равно …
Решение:
При оценке модели множественной регрессии 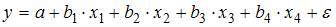 рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.
рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии 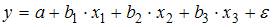 определитель матрицы парных коэффициентов корреляции между факторами
определитель матрицы парных коэффициентов корреляции между факторами  ,
,  и
и 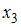 близок к единице. Это означает, что факторы
близок к единице. Это означает, что факторы 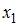 ,
, 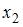 и
и 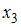 …
…
Независимы
мультиколлинеарны
количественно измеримы
значимы
Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 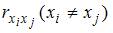 были бы равны нулю.
были бы равны нулю.
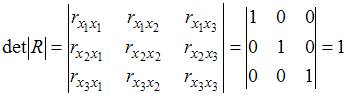 , поскольку
, поскольку 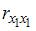 =
= 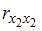 =
= 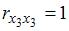 и
и 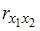 =
= 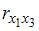 =
= 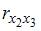 =0.
=0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
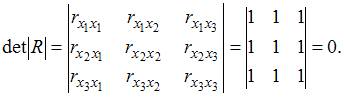
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 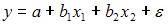 необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
x1 и x2
y и {x1; x2}
a и {b1; b2}
b1 и b2
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 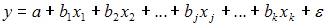 , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии); 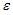 – случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2.
– случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2.
Мультиколлинеарны
независимы
количественно измеримы
значимы
Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 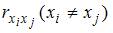 были бы равны нулю.
были бы равны нулю.
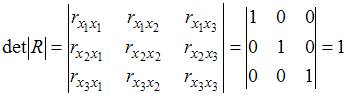 , поскольку
, поскольку 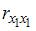 =
= 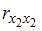 =
= 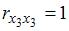 и
и 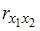 =
= 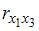 =
= 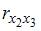 =0.
=0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
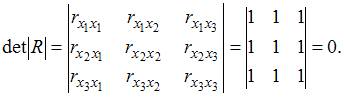
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
5. Для эконометрической модели линейного уравнения множественной регрессии вида 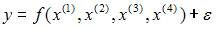 построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3), x(4)– независимые переменные):
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3), x(4)– независимые переменные):
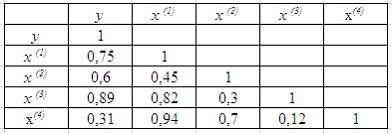
Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются …
x(2) и x(3)
x(1) и x(3)
x(1) и x(4)
x(2) и x(4)
Решение:
При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. При этом осуществляют проверку коэффициентов линейной корреляции для каждой пары независимых (объясняющих) переменных. Эти значения отражены в матрице парных коэффициентов линейной корреляции. Считается, что наличие значений коэффициентов парной корреляции между объясняющими переменными, превышающих по абсолютной величине 0,7, отражает тесную связь между этими переменными (теснота связи с переменной y в данном случае не рассматривается). Такие независимые переменные называются коллинеарными. Если значение коэффициента парной корреляции между объясняющими переменными не превышает по абсолютной величине 0,7, то такие объясняющие переменные не являются коллинеарными. Рассмотрим значения парных коэффициентов межфакторной корреляции: между x(1) и x(2) значение равно 0,45; между x(1) и x(3) – равно 0,82; между x(1) и x(4) – равно 0,94; между x(2) и x(3) – равно 0,3; между x(2) и x(4) – равно 0,7; между x(3) и x(4) – равно 0,12. Таким образом, не превышают 0,7 значения 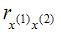 ,
, 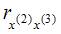 ,
, 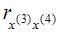 . Следовательно, коллинеарными не являютсяфакторы x(1) и x(2), x(2) и x(3), x(3) и x(4). Из последних перечисленных пар в вариантах ответов присутствует пара x(2) и x(3) – это верный вариант ответа. Для остальных пар: x(1 и x(3), x(1) и x(4), x(2) и x(4) – значения парных коэффициентов межфакторной корреляции превышают 0,7, и эти факторы являются коллинеарными.
. Следовательно, коллинеарными не являютсяфакторы x(1) и x(2), x(2) и x(3), x(3) и x(4). Из последних перечисленных пар в вариантах ответов присутствует пара x(2) и x(3) – это верный вариант ответа. Для остальных пар: x(1 и x(3), x(1) и x(4), x(2) и x(4) – значения парных коэффициентов межфакторной корреляции превышают 0,7, и эти факторы являются коллинеарными.
Тема 3: Фиктивные переменные
1. Дана таблица исходных данных для построения эконометрической регрессионной модели:
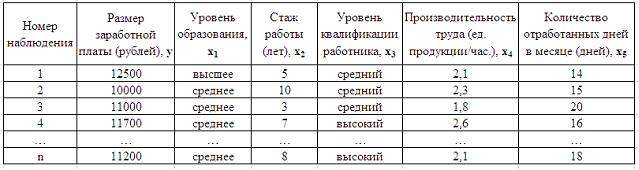 Фиктивными переменными не являются …
Фиктивными переменными не являются …
стаж работы
производительность труда
уровень образования
Изменится на (-1,67)
увеличится на 1,67
уменьшится на (-1,67)
изменится на 0,003
Решение:
Эконометрическая модель линейного уравнения регрессии имеет вид 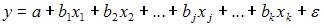 , где y – зависимая переменная, xj – независимая переменная (
, где y – зависимая переменная, xj – независимая переменная ( 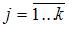 – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;
– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения; 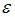 – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр bj. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной xj на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр bj. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной xj на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.
2. В уравнении линейной множественной регрессии: 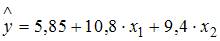 , где
, где 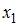 – стоимость основных фондов (тыс. руб.);
– стоимость основных фондов (тыс. руб.); 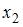 – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
– численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
на 1 тыс. руб. … уменьшится на 10,8 тыс. руб
на 1 тыс. руб. … увеличится на 10,8%
на 1% … увеличится на 10,8%
Решение:
В уравнении множественной линейной регрессии 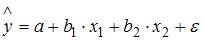 , параметр
, параметр 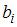 показывает среднее изменение результата y при увеличении фактора
показывает среднее изменение результата y при увеличении фактора 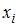 на одну единицу, при условии, что все остальные переменные останутся на постоянном уровне. В нашем случае, объем промышленного производства y характеризуется следующим уравнением
на одну единицу, при условии, что все остальные переменные останутся на постоянном уровне. В нашем случае, объем промышленного производства y характеризуется следующим уравнением 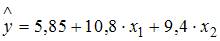 , параметр
, параметр 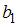 равен 10,8, следовательно, при увеличении объема основных фондов на 1 тыс. руб. объем промышленного производства увеличится на 10,8 тыс. руб. при постоянной численности занятых.
равен 10,8, следовательно, при увеличении объема основных фондов на 1 тыс. руб. объем промышленного производства увеличится на 10,8 тыс. руб. при постоянной численности занятых.
3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
0,8
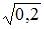
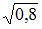
0,64
Решение:
Коэффициент детерминации 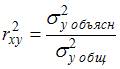 равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина (
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина ( 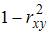 ) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
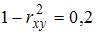 . Значит,
. Значит, 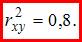
4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): 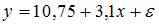 . Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
10,75
3,1
13,85
7,65
Решение:
Эконометрическая модель линейного уравнения парной регрессии имеет вид: 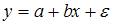 , где y – зависимая переменная, x – независимая переменная; a, b – параметры уравнения;
, где y – зависимая переменная, x – независимая переменная; a, b – параметры уравнения; 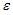 – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Значение параметра а может быть рассчитано по формуле
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Значение параметра а может быть рассчитано по формуле 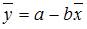 . Если
. Если 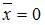 , то
, то 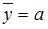 ; в таком случае говорят, что среднее значение переменной y, не зависящее от величины переменной х, равно значению параметра а. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет 10,75 рубля.
; в таком случае говорят, что среднее значение переменной y, не зависящее от величины переменной х, равно значению параметра а. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет 10,75 рубля.
5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.
факторной … остаточной
остаточной … факторной
факторной … к общей
остаточной … общей
Решение:
F-статистика рассчитывается как отношение факторной дисперсии на одну степень свободы к остаточной дисперсии на одну степень свободы.
Тема 5: Оценка параметров линейных уравнений регрессии
1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
Разность
сумма квадратов разности
квадрат разности
сумма разности квадратов
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения 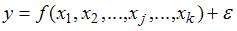 , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция); 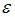 – случайные факторы. При этом
– случайные факторы. При этом 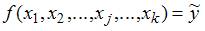 , тогда
, тогда 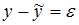 , где
, где 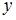 – фактическое значение зависимой переменной,
– фактическое значение зависимой переменной, 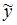 – расчетное значение зависимой переменной,
– расчетное значение зависимой переменной, 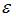 – ошибка модели. Выразим значение
– ошибка модели. Выразим значение 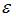 :
: 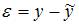 . Поэтому правильный ответ – «разность».
. Поэтому правильный ответ – «разность».
2. Величина 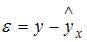 называется …
называется …
Случайной составляющей
оценкой параметра
значением параметра
переменной
Решение:
Величина 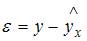 называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.
называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.
3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …
Ошибку модели
величину коэффициента регрессии
значение свободного члена уравнения
нулевое значение независимой переменной
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения 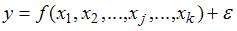 , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция); 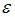 – случайные факторы. При этом
– случайные факторы. При этом 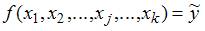 , тогда
, тогда 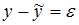 , где
, где 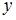 – фактическое значение зависимой переменной,
– фактическое значение зависимой переменной, 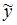 – расчетное значение зависимой переменной,
– расчетное значение зависимой переменной, 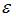 – ошибка модели. Поэтому правильный ответ – «ошибку модели».
– ошибка модели. Поэтому правильный ответ – «ошибку модели».
4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
0,2
0,8
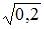
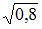
Решение:
Коэффициент детерминации 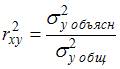 равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно,
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно, 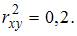
5. При методе наименьших квадратов параметры уравнения парной линейной регрессии 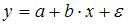 определяются из условия ______ остатков
определяются из условия ______ остатков 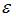 .
.
Минимизации суммы квадратов
равенства нулю суммы квадратов
минимизации модулей
равенства нулю
Решение:
При методе наименьших квадратов параметры уравнения парной линейной регрессии 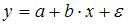 определяются из условия минимизации суммы квадратов остатков
определяются из условия минимизации суммы квадратов остатков 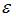 .
.
Тема 6: Предпосылки МНК, методы их проверки
1. Для обнаружения автокорреляции в остатках используется …
Положительной
отрицательной
нулевой
бесконечно малой
Решение:
Значение коэффициента автокорреляции остатков модели 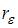 рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если
рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если 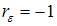 , то
, то 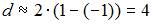 ; если
; если 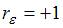 , то
, то 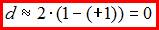 . Поэтому значение
. Поэтому значение 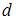 меняется от 0 до 4. Минимальное значение
меняется от 0 до 4. Минимальное значение 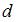 равно 0 для случая, когда
равно 0 для случая, когда 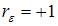 , то есть для положительной автокорреляции остатков.
, то есть для положительной автокорреляции остатков.
4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.
Гетероскедатичность
случайный характер
нулевая средняя величина
отсутствие автокорреляции
Решение:
Условия, необходимые для несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК.
Исследования остатков предполагают проверку наличия следующих пяти предпосылок МНК:
– случайный характер остатков;
– нулевая средняя величина остатков, не зависящая от 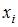 ;
;
– гомоскедастичность остатков;
– отсутствие автокорреляции остатков;
– подчинение остатков нормальному закону распределения.
Гетероскедатичность остатков не является предпосылкой МНК.
5. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле 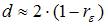 , где
, где 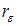 – значение коэффициента автокорреляции остатков модели. Максимальная величина значения
– значение коэффициента автокорреляции остатков модели. Максимальная величина значения 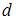 будет наблюдаться при ________ автокорреляции остатков.
будет наблюдаться при ________ автокорреляции остатков.
Отрицательной
положительной
нулевой
бесконечно малой
Решение:
Значение коэффициента автокорреляции остатков модели 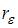 рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если
рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если 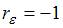 , то
, то 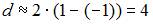 ; если
; если 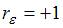 , то
, то 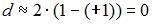 . Поэтому значение
. Поэтому значение 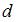 меняется от 0 до 4. Максимальное значение
меняется от 0 до 4. Максимальное значение 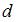 равно 4 для случая, когда
равно 4 для случая, когда 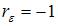 , то есть для отрицательной автокорреляции остатков.
, то есть для отрицательной автокорреляции остатков.
Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
1. Пусть 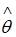 – оценка параметра
– оценка параметра 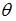 регрессионной модели, полученная с помощью метода наименьших квадратов;
регрессионной модели, полученная с помощью метода наименьших квадратов; 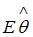 – математическое ожидание оценки
– математическое ожидание оценки 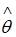 . В том случае если
. В том случае если 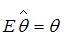 , то оценка обладает свойством …
, то оценка обладает свойством …
Несмещенности
состоятельности
эффективности
смещенности
Решение:
Желательными свойствами оценок параметров регрессионной модели являются состоятельность, несмещенность и эффективность. Понятие несмещенности оценки формулируется следующим образом: «Оценка 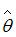 параметра
параметра 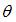 называется несмещенной, если математическое ожидание
называется несмещенной, если математическое ожидание 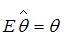 »; где
»; где 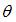 – истинное значение параметра, вычисленное для генеральной совокупности. Поэтому правильный ответ – «несмещенности».
– истинное значение параметра, вычисленное для генеральной совокупности. Поэтому правильный ответ – «несмещенности».
2. Из несмещенности оценки параметра следует, что среднее значение остатков равно …
-1
Решение:
Желательными свойствами оценок параметров регрессионной модели являются состоятельность, несмещенность и эффективность. Понятие несмещенности оценки формулируется следующим образом: «Оценка 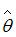 параметра
параметра 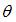 называется несмещенной, если математическое ожидание
называется несмещенной, если математическое ожидание 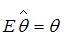 »; где
»; где 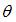 – истинное значение параметра, вычисленное для генеральной совокупности. Математическое ожидание
– истинное значение параметра, вычисленное для генеральной совокупности. Математическое ожидание 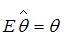 в том случае, если
в том случае, если 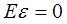 .
.
3. Несмещенность оценок параметров регрессии означает, что …
Обобщенный
косвенный
двухшаговый
трехшаговый
Решение:
При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется вместо традиционного метода наименьших квадратов применять обобщенный метод наименьших квадратов.
3. Пусть y – издержки производства, 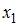 – объем продукции,
– объем продукции, 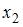 – основные производственные фонды,
– основные производственные фонды, 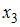 – численность работников. Известно, что в уравнении
– численность работников. Известно, что в уравнении 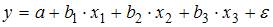 дисперсии остатков пропорциональны квадрату численности работников
дисперсии остатков пропорциональны квадрату численности работников 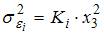 .
.
После применения обобщенного метода наименьших квадратов новая модель приняла вид 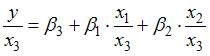 . Тогда параметр
. Тогда параметр 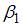 в новом уравнении характеризует среднее изменение затрат …
в новом уравнении характеризует среднее изменение затрат …
Корреляции
детерминации
регрессии
эластичности
Решение:
Заданная регрессионная модель вида 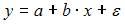 – это линейное уравнение парной регрессии, для которого показателем тесноты связи между переменными
– это линейное уравнение парной регрессии, для которого показателем тесноты связи между переменными 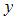 и
и 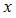 является парный коэффициент линейной корреляции.
является парный коэффициент линейной корреляции.
2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии 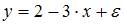 является …
является …
[–1; 0]
[0; 1]
[–1; 1]
[–2; 2]
Решение:
Коэффициент корреляции для парной линейной регрессии в общем случае изменяется в пределах [–1, 1]. Однако так как значение коэффициента регрессии отрицательное, то и значение коэффициента корреляции для уравнения тоже будет отрицательным, значит, самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии 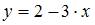 будет [–1; 0].
будет [–1; 0].
3. Самым коротким интервалом изменения показателя множественной корреляции для уравнения множественной линейной регрессии 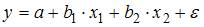 , если известны парные коэффициенты корреляции
, если известны парные коэффициенты корреляции 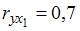 ,
, 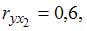 является интервал …
является интервал …
[0,7; 1]
[0; 1]
[0,6; 0,7]
[-1; 1]
Решение:
Показатель множественной корреляции изменяется в пределах [0; 1]. Однако величина индекса множественной корреляции должна быть больше максимального парного индекса корреляции или равна ему 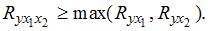 Следовательно, самым коротким интервалом изменения показателя множественной корреляции будет [0,7; 1].
Следовательно, самым коротким интервалом изменения показателя множественной корреляции будет [0,7; 1].
4. Для регрессионной модели вида 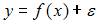 получена диаграмма
получена диаграмма
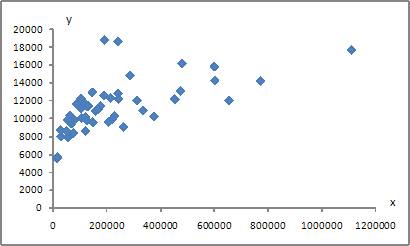
Такое графическое отображение называется …
Полем корреляции
диаграммой детерминации
полем детерминации
коррелограммой
Решение:
Графическое отображение совокупности точек с координатами 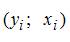 на плоскости для зависимости
на плоскости для зависимости 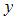 от
от 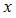 называется полем корреляции, или диаграммой рассеяния. Поэтому верный ответ – «полем корреляции».
называется полем корреляции, или диаграммой рассеяния. Поэтому верный ответ – «полем корреляции».
0,9
0,19
0,81
0,95
Решение:
Известно, что доля остаточной регрессии в общей составила 0,19. Значит, 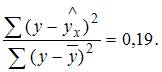 Найдем коэффициент детерминации:
Найдем коэффициент детерминации: 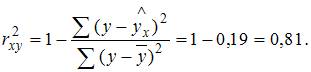 Вычислим коэффициент корреляции:
Вычислим коэффициент корреляции: 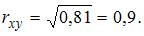
2. Известно, что общая сумма квадратов отклонений 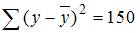 , а остаточная сумма квадратов отклонений,
, а остаточная сумма квадратов отклонений, 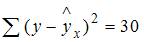 . Тогда значение коэффициента детерминации равно …
. Тогда значение коэффициента детерминации равно …
0,8
0,2
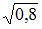
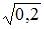
Решение:
Для расчета коэффициента детерминации можно пользоваться следующей формулой: 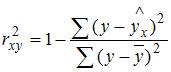 . Значит, в нашем случае коэффициент детерминации равен:
. Значит, в нашем случае коэффициент детерминации равен: 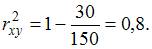
3. Для регрессионной модели вида 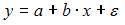 , где
, где 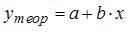 рассчитаны дисперсии:
рассчитаны дисперсии: 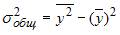 ;
; 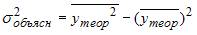 ;
; 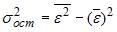 . Тогда величина
. Тогда величина 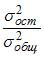 характеризует долю …
характеризует долю …
Остаточной дисперсии
коэффициента детерминации
коэффициента корреляции
объясненной дисперсии
Решение:
Значение коэффициента детерминации 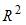 характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность
характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность 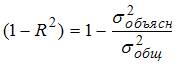 характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле
характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле 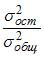 . Поэтому отношение
. Поэтому отношение 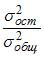 характеризует долю остаточной дисперсии.
характеризует долю остаточной дисперсии.
4. Если общая сумма квадратов отклонений 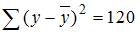 , и остаточная сумма квадратов отклонений
, и остаточная сумма квадратов отклонений 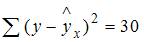 , то сумма квадратов отклонений, объясненная регрессией, равна …
, то сумма квадратов отклонений, объясненная регрессией, равна …
0,25
Решение:
Общая сумма квадратов отклонений складывается из суммы квадратов отклонений, объясненных регрессией, и остаточной сумма квадратов отклонений.
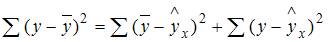
Значит, сумма квадратов отклонений, объясненная регрессией, равна разности общей сумме квадратов отклонений и остаточной суммы квадратов отклонений.
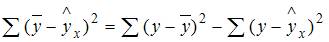
Получается 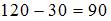 .
.
Тема 11: Проверка статистической значимости эконометрической модели
1. При расчете скорректированного коэффициента множественной детерминации пользуются формулой 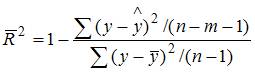 , где …
, где …
n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
m – число наблюдений; n – число факторов, включенных в модель множественной регрессии
n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии
n – число параметров при независимых переменных; m – число наблюдений
Решение:
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и имеет вид 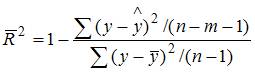 , где n – число наблюдений, m – число факторов, включенных в модель множественной регрессии.
, где n – число наблюдений, m – число факторов, включенных в модель множественной регрессии.
2. Если известно уравнение множественной регрессии 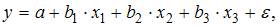 построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …
построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …
766,67
877,45
Решение:
Расчет F-статистики начинается с разложения общей суммы квадратов отклонений на сумму квадратов отклонений, объясненную регрессией, и остаточную сумму квадратов отклонений:
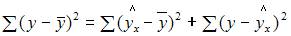 , где
, где
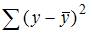 – общая сумма квадратов отклонений
– общая сумма квадратов отклонений
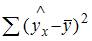 – сумма квадратов отклонений, объясненная регрессией
– сумма квадратов отклонений, объясненная регрессией
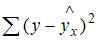 – остаточная сумма квадратов отклонений
– остаточная сумма квадратов отклонений
В нашем случае дано 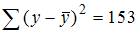 ,
, 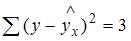 . Следовательно,
. Следовательно, 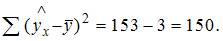
Существует равенство между числом степеней свободы общей, факторной и остаточной сумм квадратов отклонений:
n – 1 = m + (n – m – 1), где n –число наблюдений, m – число параметров перед переменными в уравнений регрессии.
Число степеней свободы для общей суммы квадратов отклонений равно n – 1. В нашем случае n – 1 = 49.
Число степеней свободы для остаточной суммы квадратов отклонений равно n – m – 1 = 46.
Число степеней свободы для факторной суммы квадратов отклонений равно m = 3.
Рассчитаем факторную и остаточную дисперсии на одну степень свободы по формулам 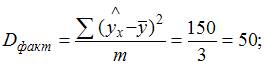
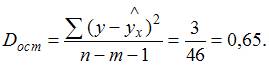
F-статистика вычисляется по формуле 
3. Для регрессионной модели известны следующие величины дисперсий:
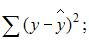
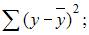
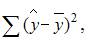 где y – значение зависимой переменной по исходным данным;
где y – значение зависимой переменной по исходным данным; 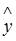 – значение зависимой переменной, вычисленное по регрессионной модели;
– значение зависимой переменной, вычисленное по регрессионной модели; 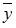 – среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
– среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
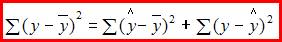
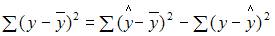
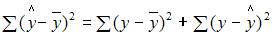
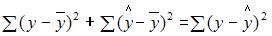
Решение:
Назовем приведенные дисперсии: 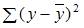 – общая дисперсия;
– общая дисперсия; 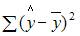 – объясненная дисперсия;
– объясненная дисперсия; 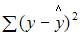 – остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство:
– остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство: 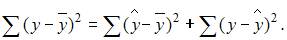
Тема 12: Оценка значимости параметров эконометрической модели
