РАСЧЕТНО-ГРАФИЧЕСКАЯРАБОТА№4

РАСЧЕТПЛОСКОЙСТАТИЧЕСКИНЕОПРЕДЕЛИМОЙ

РАМЫМЕТОДОМПЕРЕМЕЩЕНИЙ

Литература: [2,c.3–21],[3,c.380–419],[4,c.187–203],

[5,c. 398–413], [6,c.202–223].

Исходныеданныекработеопределяютсяпотабл.4.1исхемам,представленнымнарис.4.1.

Таблица 4.1

Исходные данные к РГР № 4

Первая цифра шифра	F1, кН	F2, кН	Вторая цифра шифра	q1, кН/м	q2, кН/м	Третьяцифрашифра (№схемы)	l, м	h, м	α

Последовательностьрасчета

4.1.Вычертитьвмасштаберасчетнуюсхемурамысуказаниемразмеров,величиннагрузокисоотношенийжесткостей.

4.2.Определитьстепенькинематическойнеопределимостирамы(числонеизвестныхметодаперемещений)n_к=n_у+n_л,гдеn_у−числожесткихузловрасчетнойсхемы,способныхкповоротуприеедеформации;n_л−числовозможныхлинейныхсмещенийвсехузловрасчетнойсхемы.

Рис.4.1.СхемызаданийкРГР№4

4.3.Получитьосновнуюсистемуметодаперемещений,введядополнительныесвязипонаправлениямвозможныхугловповоротажесткихузловилинейныхсмещенийвсехузлов

Расчетвклассическойформе

4.4.Записатьсистемуканоническихуравненийметодаперемещенийвобщемвидеприменительнокзаданнойсхемерамы.

4.5.Построитьвосновнойсистемеметодаперемещенийдеформированныесхемыотпоследовательныхединичныхсмещенийпонаправлениюдополнительных связей.

4.6.Используятаблицыреакций(пп.1–4прил.1),построитьвосновнойсистемеэпюры 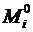отуказанныхвп.4.5единичныхсмещений.

4.7.Используятаблицыреакций(пп.5–8прил.1),построитьвосновнойсистемеэпюру 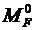отзаданногозагружения.

4.8.Определитькоэффициентыпринеизвестных(реакциивдополнительныхсвязяхотединичныхсмещений)исвободныечлены(реакциивдополнительныхсвязяхотдействиявнешнейнагрузки)системыканоническихуравнений.

Указания:

· Реакциивдополнительныхугловыхсвязяхопределяютсянепосредственноизравновесияжесткогоузла,вкоторыйвведенаугловаясвязь.

· Реакциивдополнительныхлинейныхсвязяхортогональныхрамопределяютсяизусловияравновесияотсеченнойчастиосновнойсистемы.Приэтомсечения(сквозныеилизамкнутые)проводятсяпараллельноосилинейнойсвязичерезвсестержнисхемы,получившиедеформации(см.п.4.4)присмещенииданнойсвязи.

· Реакциявдополнительнойсвязисчитаетсяположительной,еслионанаправленавсторонузаданноговп.4.4.смещенияэтойсвязи.

· Всесхемыпоопределениюреакцийвдополнительныхсвязяхдолжныбытьприведеныначертеже.

4.9.ЗаписатьсистемуканоническихуравненийметодаперемещенийвчисленномвидеиизеерешениянайтинеизвестныеZ_i.

4.10.Определитьизгибающиемоментывосновнойсистемеотдействительныхсмещенийпонаправлениюдополнительных связей (построить эпюры)инаоснованиипринципанезависимостидействиясилпостроитьэпюруизгибающихмоментоввзаданнойрасчетнойсхеме

.

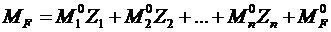4.11.Произвестипроверкиправильностипостроенияэпюры:

·Длякаждогожесткогоузлазаданнойрасчетнойсхемыдолжновыполнятьсяуравнениеравновесия.

· Длявсейрамыдолжнавыполнятьсядеформационнаяпроверкарасчета.Дляэтоговыбираетсялюбаянаиболеепростаястатическиопределимаяосновнаясистема,получаемаяиззаданнойпутемудалениялишнихсвязей.Ввыбраннойстатическиопределимойосновнойсистеместроитсясуммарнаяэпюраизгибающихмоментов 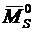отединичныхсил,приложенныхпонаправлениюудаленныхсвязей.Проверкасчитаетсявыполненной,если

.

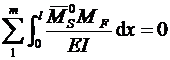4.12.ПостроитьэпюрупоперечныхсилвзаданнойрасчетнойсхеменаоснованиидифференциальнойзависимостиQ_F=dM/dx.

4.13.ОпределитьпродольныесилывовсехстержняхрасчетнойсхемыизусловияравновесияееузловипостроитьэпюруN_F.

4.14.Произвестистатическуюпроверкурасчета:любаяотсеченнаячастьрасчетнойсхемыиливсясхема,отсеченнаяотопор,поддействиемвнутреннихивнешнихсилдолжнанаходитьсявравновесии,т.е.должнывыполнятьсятриуравненияравновесия 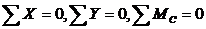(c–любаяточканаплоскости).

Длявыполненияэтойпроверкирекомендуетсярассмотретьдваслучая:

· Равновесиевсейрасчетнойсхемы,отсеченнойотопор.

· Равновесиелюбойотсеченнойчастирасчетнойсхемы

Расчетвматричнойформе[1]

4.15.Вычертитьосновнуюсистемуметодаперемещений(п.4.2)инанейпоказатьпорядокобходастержнейрасчетнойсхемыипронумероватьрасчетныесечениявсоответствииснамеченнымобходом.

4.16.Составитьматрицыжесткостиотдельныхстержнейрамы:

· дляучастковcоднимрасчетнымсечением

;

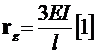· дляучастковсдвумярасчетнымисечениями

.

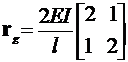4.17.Составитьквазидиагональнуюматрицужесткостинеобъединенныхэлементов 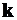(mxm),гдеm–числорасчетныхсеченийрамы.Вобщемвидеэтаматрицаимеетвид

.

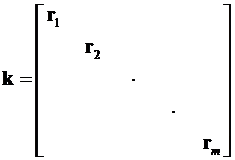4.18.Подеформированнымсхемам,построеннымвосновнойсистемеотединичныхсмещенийпонаправлениюдополнительныхсвязей(п.4.4),определитьуглыповоротарасчетныхсеченийисоставитьматрицупреобразованиядеформаций 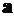порядка(mxn),гдеn–числонеизвестныхметодаперемещений.

4.19.Поэпюре(см.п.4.6)составитьматрицуусилийвосновнойсистемеметодаперемещений 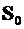(m´p),гдеp–числовариантовзагружения(дляданнойРГРp=1).

4.20.Составитьматрицу 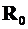свободныхчленовсистемыканоническихуравнений(nxp),используярезультатырасчетавклассическойформе(см.п.4.7).

4.21.Выполнитьнижеперечисленныематричныеоперации.

· Транспонироватьматрицу .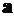

· Получитьматрицуусилийврасчетныхсеченияхосновнойсистемыотединичныхсмещенийпонаправлениюдополнительныхсвязей

.

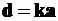· Получитьматрицукоэффициентовпринеизвестных

.

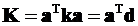· Выполнитьобращениематрицы 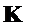ипроизвестипроверкуобращения

,

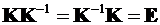где 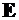–единичнаяматрица.

· Определитьнеизвестные метода перемещений

.

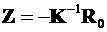· Определитьусилиявосновнойсистемеметодаперемещенийотдействительныхсмещенийпонаправлениюдополнительныхсвязей

.

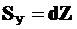· Получитьматрицуусилийвзаданнойрасчетнойсхеме

.

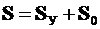· Сравнитьзначенияэлементовматрицы 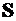,сусилиями,полученнымиклассическойформойрасчета(п.4.10).

4.22. Произвестипроверкуправильностипроизведенногорасчета.Дляэтогопоэпюре 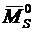(см.п.4.11)составитьматрицуусилий .

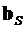Деформационнаяпроверкарасчетавматричномвидебудетиметьвид:

,

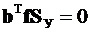где 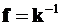─ матрицаподатливостинеобъединенныхэлементоврасчетнойсхемы.

РАСЧЕТНО-ГРАФИЧЕСКАЯ№5

ДИНАМИЧЕСКИЙРАСЧЕТПЛОСКОЙРАМЫ

СКОНЕЧНЫМЧИСЛОМСТЕПЕНЕЙСВОБОДЫНАДЕЙСТВИЕВИБРАЦИОННОЙНАГРУЗКИ

Литература:[2,c.178–197],[8,c.124–220],[9,c.3–61],

[11,c.54–65,69–82].

Исходныеданныекработеопределяютсяпотабл.5.1исхемам,представленнымнарис.5.1.

Таблица 5.1

Исходные данные к РГР № 5

Первая цифра шифра	m, т	β	Вторая цифра шифра		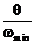α	F1, кН	F2, кН	Третья цифра шифра (№схемы)	l, м	h, м	EI1, кН·м2
	0,5			0,5	1,5
	0,6	1,5		0,55
	0,7			0,6	2,5
	0,8	2,5		0,65
	0,9			0,7	1,5
	1,0			0,68
	1,1	1,5		0,8	2,5
	1,2			0,72
	1,3	2,5		0,66	3,5
	1,4			0,58

Примечание.ВтаблицеприведеныамплитудныезначениявибрационнойнагрузкиF_i(t)=F_isinθt.

Последовательностьрасчета

5.1.Вычертитьвмасштабезаданнуюрасчетнуюсхемурамысуказаниемразмеров,величинмасс,вибрационнойнагрузкиисоотношенияжесткостейстержней.

5.2.Определитьчислостепенейсвободысосредоточенныхмассзаданнойрасчетнойсхемы.

Рис.5.1.СхемызаданийкРГР№5

5.3.Показатьрасчетнуюсхемурамыпридействииамплитудныхзначенийинерционныхсиливибрационнойнагрузки.

5.4.Записатьвобщемвидеуравнениечастотсвободныхколебанийприменительнокзаданнойрасчетнойсхеме.

5.5.ПонаправлениювозможныхсмещениймасспоследовательноприложитьединичныесилыиотдействиякаждойизнихпостроитьэпюрыизгибающихмоментовM_i.

5.6.Определитькоэффициентыуравнениячастот

,

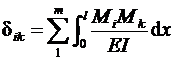гдеm–числоучастковинтегрирования.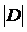

5.7.Составитьуравнениечастотвчисленномвиде.

5.8.Определитькорничастотногоуравненияl_i(i=1…n)ипроизвестипроверкиправильностиегорешения:

,

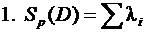гдеS_p(D)–след(суммаглавныхкоэффициентов)матрицы,составленной из коэффициентов частотного уравнения;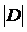– величина определителя этой матрицы

5.9.Определитьчастотыипериодысвободныхколебаниймасс.

5.10.Вычислитьотносительныеамплитудымассипостроитьформыколебанийдлякаждойчастоты.

5.11.Изопределенноговп.5.7спектрачастотсвободныхколебанийвыявитьнаименьшеезначениеω_minиопределитькруговуючастотувынужденныхколебанийпозаданномувтабл.5.1соотношению.

5.12.Показатьрасчетнуюсхемурамыпридействиинанееамплитудныхзначенийнагрузокиинерционныхсил.

5.13.Записатьвобщемвидесистемуканоническихуравненийдляопределенияамплитудныхзначенийинерционныхсилприменительнокзаданнойрасчетнойсхеме.

5.14.ПостроитьвзаданнойрасчетнойсхемеэпюруизгибающихмоментовM_Fотдействияамплитудныхзначенийвибрационной нагрузки.

5.15.Определитьглавныекоэффициентысистемыканоническихуравнений

.

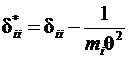Побочныекоэффициентысистемыканоническихуравненийимеюттежезначения,чтоивуравнениичастот.

5.16.Определитьсвободныечленысистемыканоническихуравнений

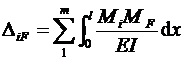
5.17.ЗаписатьсистемуканоническихуравненийвчисленномвидеиизеерешенияопределитьамплитудныезначенияинерционныхсилJ_i.

5.18.Построитьдинамическуюэпюруизгибающихмоментов

M_дин=M₁J₁+M₂J₂+…+M_nJ_n+M_F.

5.19.Определитьамплитудымассa_i=J_i/m_i∙θ²ипостроитьдеформированнуюсхемурамыпривынужденныхколебаниях.