Точные решения дифференциального уравнения упругого режима
Дифференциальное уравнение упругого режима фильтрации можно записать
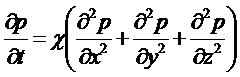 (5.126)
(5.126)
Интегрируя дифференциальное уравнение (5.126) при заданных начальном и граничных условиях, определяют давление в любой точке пласта в любой момент времени.
Решение задачи перераспределения давления после пуска скважины с постоянным дебитом Q в бесконечном горизонтальном пласте сводится к интегрированию дифференциального уравнения (5.126), имеющего для плоскорадиальной фильтрации вид
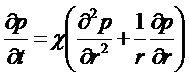 (5.I27)
(5.I27)
с начальным и граничными условиями:
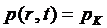 при t=0
при t=0
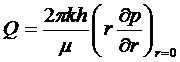 (5.I28)
(5.I28)
Точное решение этой задачи при rс=0 дается формулой
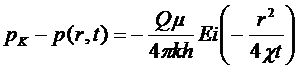 (5.129)
(5.129)
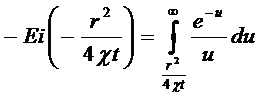 (5.130)
(5.130)
Эта табулированная функция называется интегральным экспоненциалом, или интегральной показательной функцией.
При малых значениях аргумента 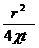 функцию-
функцию- 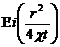 приближенно заменить формулой
приближенно заменить формулой
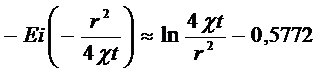 (5.131)
(5.131)
и тогда
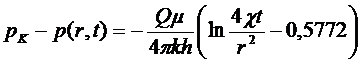 (5.132)
(5.132)
Формула (5.129) является основной формулой упругого режима пластов, широко применяющейся при исследовании процесса перераспределения пластового давления, вызванного пуском скважин с постоянными дебитными, остановкой скважин, изменениями темпов добычи и т. д.
Формулу (5.129) также можно использовать в случае притока жидкости к скважине конечного радиуса и в начальной стадии изменения давления в пласте конечных размеров.
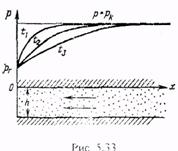
При неустановившейся параллельно-струйной фильтрации упругой жидкости к галерее, расположенной в полосообразном полубесконечном пласте перпендикулярно к оси ОХ в сечении х=0 (рис.5.33) и эксплуатирующейся с постоянным давлением на забое галереи рг, давление в любой точке пласта в любой момент времени получим, интегрируя уравнение
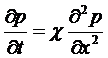 (5.133)
(5.133)
при начальном и граничных условиях:
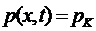 при t=0.
при t=0.
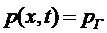 при x=0.
при x=0.
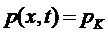 при x=∞
при x=∞
Решение выражается формулой
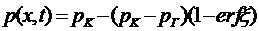 (5.135)
(5.135)
где
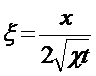
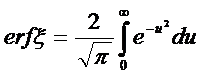 (5.136)
(5.136)
-интеграл вероятности
Приближенные методы решений
В связи со сложностью точных решений были предложены различные приближенные методы решения задач неустановившейся фильтрации упругой жидкости. Одним из наиболее распространенных приближенных методов является метод последовательной смены стационарных состояний. Этот метод заключается в том, что в какой-то момент времени зона пониженного давления (возмущенная зона) считается распространенной на определенное расстояние l=1(t) (приведенный радиус влияния) и предполагается, что во всей возмущенной зоне давление распределяется так, как будто движение жидкости установившееся. В действительности же распределение давления в пласте не будет стационарным и зона пониженного давления захватит теоретически весь пласт. Закон изменения во времени приведенного радиуса влияния l(t) определяется из условия материального баланса. При неустановившемся притоке упругой жидкости к галерее 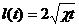 если отбор проводится при постоянной депрессии pK-pг=const;
если отбор проводится при постоянной депрессии pK-pг=const; 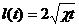 ,если задан постоянный дебит Q(0, t)=const
,если задан постоянный дебит Q(0, t)=const
При плоскорадиальном притоке упругой жидкости к скважине можно считать с точностью до 10-15%, что 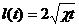 (если l(t)>>rc) как для случая постоянной депрессии, так и для постоянного отбора.
(если l(t)>>rc) как для случая постоянной депрессии, так и для постоянного отбора.
В методе А.М.Пирвердяна, который развивает метод последовательной смены стационарных состояний, эпюра давления задается так, чтобы она не имела угловых точек. Например, при притоке к галерее распределение давления по пласту задается в виде параболы, касательная к которой в точке x=l(t) горизонтальна (рис.5.34).
Если отбор жидкости не меняется с течением времени, т. е.
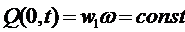
то
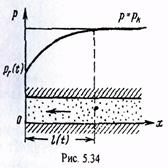
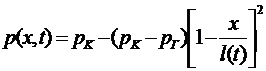 (5.137)
(5.137)
где
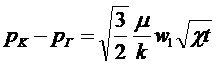 (5.138)
(5.138)
а приведенный радиус влияния, найденный из уравнения материального баланса, определяется по формуле
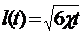 (5.139)
(5.139)
