Границы применимости закона Дарси. Нелинейные законы фильтрации

Подобно тому, как в трубной гидравлике критерием режима движения служит число Рейнольдса

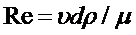(5,1)

в теории фильтрации вводится безразмерный параметр

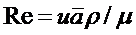(5,2)

где и - некоторая характерная скорость; а - линейный параметр, характеризующий среднее сечение поровых каналов; ρ - плотность жидкости; μ - динамический коэффициент вязкости.

Скорость фильтрации, при которой нарушается закон Дарси, называется критической скоростью фильтрации (u_кр).

Однако нарушение линейного закона фильтрации еще не означает перехода от ламинарного движения к турбулентному. Закон Дарси нарушается вследствие того, что силы инерции, возникающие в жидкости за счет извилистости каналов и изменения площади их поперечных сечений, становятся при u> u_кр соизмеримыми с силами трения.

В трубной гидравлике значение Re, при котором происходит смена режимов, равно Reкр= 2320, в теории фильтрации закон Дарси имеет место при значении безразмерного параметра Re, меньшего критического (Re_кр), которое устанавливается из опыта.

Впервые число Рейнольдса для фильтрации жидкости было введено Н.Н.Павловским в виде

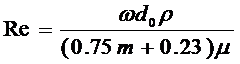(5,3)

т. е. за характерную скорость была взята скорость фильтрации u, а линейный параметр представлен выражением

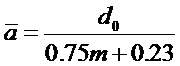(5,4)

Критические значения Re по Павловскому заключены в интервале

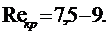
В.Н.Щелкачев предложил взять за линейный параметр выражение, пропорциональное корню квадратному из коэффициента проницаемости,

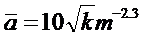(5.5)

Число Рейнольдса по В.Н.Щелкачеву имеет вид

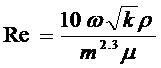(5,6)

а критические значения лежат в интервале

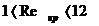
По М.Д.Миллионшикову за характерную скорость взята средняя скорость движения жидкости

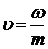
а за линейный параметр – выражени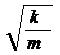е ,т.е

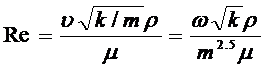
0,022 < Re_кр< 0,29.

Если вычисленное по одной из формул (5.3), (5.6), (5.7) значение числа Re оказывается меньше нижнего критического значения Re_кр, то закон Дарси справедлив, если Re больше верхнего значения Re_кр, то закон Дарси заведомо нарушен.

Широкий диапазон изменения Re_кр объясняется тем, что формулы для числа Re входят параметры k и т. которые не полностью характеризуют микроструктуру породы. Как следует из опытов, для каждой горной породы можно указать более узкий диапазон значений Re_кр.

Определение режима фильтрации жидкостей и газов имеет большое практическое значение, ибо без знания закона фильтрации в пласте нельзя правильно рассчитать дебиты скважин, распределение давления в пласте, а также невозможно определение параметров пласта (k, h, т и др.) по данным исследования нефтяных и газовых скважин.

При нарушении закона Дарси зависимость между скоростью фильтрации и градиентом давления dp/ds лучше всего описывается двучленной формулой

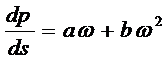(5,8)

которая выражает плавный переход от линейного закона фильтрации к нелинейному. При малых значениях скорости aω>>bω²пренебрегаем вторым членом и получаем закон Дарси; при значениях , ω≥ω_кр слагаемые aω и bω²имеют один и тот же порядок; при больших скоростях фильтрации aω<<bω²и можно принять

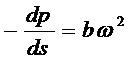(5,9)

что соответствует квадратичному закону сопротивления и имеет место при фильтрации в крупнозернистых и трещиноватых породах. Формула (5.9) называется формулой А.А. Краснопольского.

Коэффициенты a и b определяются либо экспериментально, либо поформуле a=μ/k, а b- приближенно по формуле, предложенной А.И. Ширковским

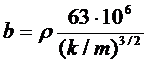(5.10)

где ρ - плотность в кг/м³; k - коэффициент проницаемости в мкм²; т - коэффициент пористости в долях единицы.

Можно записывать закон фильтрации, отличный от закона Дарси, в виде одночленной степенной зависимости между скоростью фильтрации и градиентом давления:

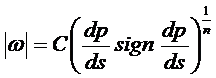(5,11)

где sign - знак производной dp/ds; С и n- некоторые постоянные, определяемые опытным путем, причем 1<п<2, п=2 соответствует закону Краснопольского.

Используя принцип однородности размерностей, можно найти выражение для коэффициента С:

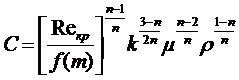(5,12)

где ƒ(m)=10m^-2.3