Определенный интеграл. Условия существования

Определенного интеграла. Свойства определенного интеграла.

Задача о поиске площади криволинейной трапеции приводит к понятию определенного интеграла. Криволинейная трапеция ограничена осью Ох, непрерывной функцией y=f(x), прямыми x=a и x=b, т.е. трапеция расположена над осью Ох. Разделим основание трапеции ¾ интервал [a,b] на n частичных интервалов [x₀,x₁],[x₁,x₂],…,[x_n-1,x_n], где a=x₀<x₁<x₂<…<x_n-1<x_n=Проведя в точках деления [a,b] прямые, параллельные оси ординат, разобьем криволинейную трапецию на n частичных трапеций. В каждом частичном интервале возьмем точки x₁,x₂,…,x_т, так что

x₀£x₁£x₁, x₁£x₂£x₂, …, x_n-1£x_n£x_n.

Рассмотрим значения ¦(x₁),¦(x₂),…,¦(x_n) и т.д.

В результате, сложив площади всех частичных трапеций, получим площадь криволинейной трапеции

S= 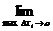S_n= 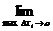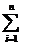¦(x_i)Dx_i, где Dx_i=x_i-x_i-1.

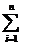¦(x_i)Dx_i называется n-й интегральной суммой.

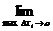
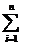¦(x_i)Dx_i= 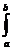¦(x)dx называется определенным интегралом, a-нижний предел интегрирования, b- верхний предел интегрирования.

Определенным интегралом называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала.

Теоремасуществования определенного интеграла. Если функция ¦(x) непрерывна в замкнутом интервале [a,b], то ее n-я интегральная сумма стремится к пределу при стремлении к нулю длины наибольшего частичного интервала. Этот предел, т.е. определенный интеграл 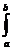¦(x)dx, не зависит от способа разбиения интервала интегрирования на частичные интервалы и от выбора в них промежуточных точек.

Свойства определенного интеграла.

Теорема 1(об интеграле суммы). Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых функций:

_,

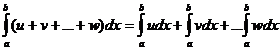где u,v,…,w – функции независимой переменной x.

Теорема 2 (о вынесении постоянного множителя). Постоянный множитель подынтегральной функции можно вынести за символ интеграла:

,

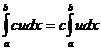где u – функция аргумента x, с – константа.

Теорема 3(о перестановке пределов). Если верхний и нижний пределы интеграла поменять местами, то интеграл изменит только знак:

.

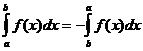Если a=b, то 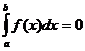, так как .

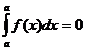Теорема 4(о разбиении интервала интегрирования). Если интервал интегрирования [a,b] разбит на две части [a,c] и [c,b], то

.

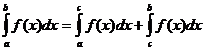Формула Ньютона-Лейбница.

Замена переменных и интегрирование по частям в

Определенном интеграле.

Формула Ньютона – Лейбница.

ТеоремаЗначение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интеграла:

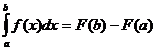, где F¢(x)=f(x) (2)

Равенство (2) называется формулой Ньютона – Лейбница.

Пример. = .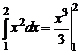

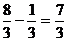Интегрирование по частям и замена переменной в определенном интеграле.

1. Формула интегрирования по частям:

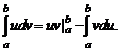
2.Формула замены переменной (подстановки):

Пусть x=y(u), тогда справедлива формула

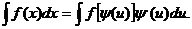
Если в интервале [u₁, u₂] функции x=y(u), y¢(u) и ¦[y(u)] непрерывны и y(u₁)=x₁, y(u₂)=x₂, то

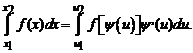
Несобственные интегралы.

Когда нами было введено понятие определенного интеграла, мы предполагали, что интервал интегрирования имеет конечную длину, а также необходимым условием интегрируемости является ограниченность функции. На этом занятии мы обобщим понятие определенного интеграла на случаи неограниченного интервала интегрируемости и на случай неограниченной функции. Такие интегралы называются несобственными интегралами. Интеграл по неограниченному промежутку интегрирования называется несобственным интегралом I рода, а интеграл от неограниченной функции – несобственным интегралом II рода.

Несобственным интегралом от функции f(x) в интервале [a;¥] называется предел интеграла 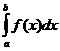при b®¥, то есть

.

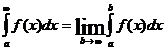Если указанный предел существует, то несобственный интеграл называется сходящимся, а если не существует, то расходящимся.

С помощью формулы Ньютона – Лейбница получаем

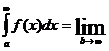[F(b)-F(a)]=F(¥)-F(a) на интервале [a,¥),

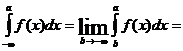F(a)-F(-¥) на интервале (-¥;a].

Если функция f(x) определена и непрерывна на всей числовой оси, то можно рассматривать несобственный интеграл в интервале (-¥+¥)

.

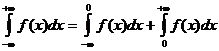Если оба интеграла в правой части сходятся, то интеграл 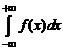называется сходящимся.

Если первообразная F(x) известна, то

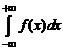=F(+¥)-F(-¥),

где F(+¥)= 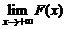, F(-¥)= .

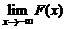Если хотя бы один из этих пределов не существует, то несобственный интеграл расходится.

Пример. Интеграл 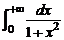сходится, так как

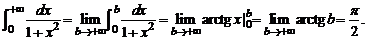
Интеграл 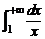расходится, так как

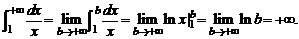
Для исследования на сходимость интегралов можно воспользоваться следующим признаком.

Признак сравнения. Пусть для всех x выполнено 0£f(x)£j(x). Тогда: 1) если сходится интеграл 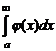, то сходится и интеграл ;

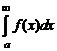3. если расходится интеграл 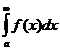, то расходится интеграл .

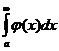Несобственные интегралы играют важную роль в различных разделах математики и ее приложениях, так, например, интеграл вида 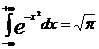называется интегралом Пуассона и играет важную роль в теории вероятности.