Лекция 5. Определенный интеграл

Задача о площади криволинейной трапеции.

Рассмотрим криволинейную трапецию, образованную отрезком 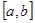оси OX (основание трапеции), прямыми 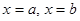(на них лежат боковые

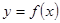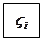
стороны трапеции) и графиком функции . Так как график функции – кривая линия, то такая трапеция называется криволинейноq й.

Устроим разбиение отрезка 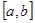точками 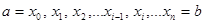. Обозначим 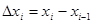. На каждом отрезке 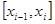отметим точку 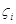. Вычислим 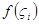. Обозначим 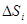- площадь части криволинейной трапеции над отрезком 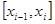, S – площадь всей криволинейной трапеции. Тогда

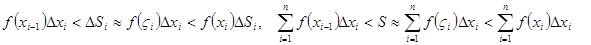Пусть функция 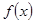непрерывна на каждом отрезке 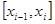. По второй теореме Вейерштрасса выполняется неравенство 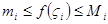, где 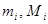- нижняя и верхняя грани функции на отрезке 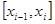. Тогда

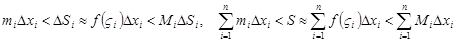
Сумма 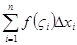называется интегральной суммой, суммы 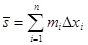, 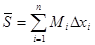называются соответственно нижней и верхней суммами Дарбу.

Будем измельчать разбиение так, чтобы 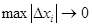. Если существует предел интегральных сумм при неограниченном измельчении разбиения, то он называется определенным интегралом (по Риману) от функции 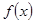по отрезку : .

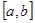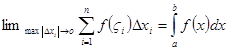Если существуют пределы нижней и верхней сумм Дарбу при неограниченном измельчении разбиения, то они называются нижним 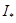и верхним 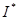интегралами Дарбу.

Критерий существования определенного интеграла. Для того, чтобы существовал определенный интеграл по Риману 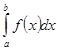, необходимо и достаточно, чтобы существовали и были равны нижний и верхний интегралы Дарбу.

Следствие.Если определенный интеграл существует как предел интегральных сумм, то он не зависит

2) от выбора разбиения, лишь бы .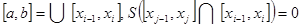

3) от выбора отмеченных точек 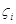на элементах разбиения

4) от способа измельчения разбиения, лишь бы .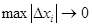

Поэтому (критерий Римана) для интегрируемости по Риману ограниченной на отрезке функции необходимо и достаточно, чтобы существовало некоторое конкретное разбиение отрезка, на котором 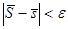для любого .

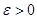Теорема. Если функция непрерывна на отрезке, то она интегрируема на этом отрезке.

Теорема.Если функция кусочно непрерывна на отрезке (имеет на нем не более конечного числа разрывов первого рода), то она интегрируема на этом отрезке.

Мы пришли к определенному интегралу от задачи о площади криволинейной трапеции. Если функция принимает на отрезке неотрицательные значения, то определенный интеграл можно интерпретировать как площадь под графиком функции. В этом состоит геометрический смысл определенного интеграла.

К понятию интеграла можно придти и от других задач. Например, от задачи о работе переменной по величине силы, не меняющей направления на прямолинейном пути, от задачи о массе отрезка, плотность которого меняется от точки к точке, от задачи о пути тела, движущегося прямолинейно с переменной скоростью. Фактически, все эти задачи формально сводятся к задаче о площади криволинейной трапеции. В задаче о работе силы по оси ординат откладываются значения скалярного произведения вектора силы в данной точке x отрезка на орт оси OX. В задаче о массе отрезка по оси ординат откладываются значения переменной плотности. В задаче о пути, пройденном телом, по оси ординат откладывается величина скорости тела в данной точке.

К схеме определенного интеграла сводится любая задача вычисления некоторой величины, аддитивно зависящей от множества, т.е. величины I, удовлетворяющей соотношению 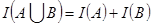, где А, В – отрезки оси OX (в общем случае определенного интеграла по некоторому множеству А, В – некоторые множества). В качестве таких величин можно выбрать длину отрезка, длину кривой, площадь поверхности, объем пространственного тела, массу указанных множеств и т.д.