Определенный интеграл
Задача о площади криволинейной трапеции.
Пусть функция 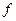 определена на отрезке
определена на отрезке  . Разобьем этот отрезок на части точками
. Разобьем этот отрезок на части точками 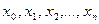 такими, что
такими, что 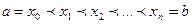 . Получим разбиение
. Получим разбиение 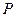 , состоящее из частичных отрезков
, состоящее из частичных отрезков 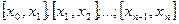 На каждом частичном отрезке
На каждом частичном отрезке 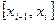 длиной
длиной 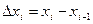 выберем произвольно точку
выберем произвольно точку 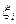
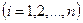 и назовем такое разбиение
и назовем такое разбиение 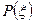 , где через
, где через 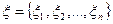 обозначен набор выбранных точек
обозначен набор выбранных точек 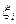 , разбиением с отмеченными точками. Легко видеть, что даже для одного и того же разбиения
, разбиением с отмеченными точками. Легко видеть, что даже для одного и того же разбиения 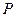 , представляющего собой множество точек
, представляющего собой множество точек 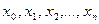 , можно построить бесконечно много разбиений с отмеченными точками только за счет выбора точек
, можно построить бесконечно много разбиений с отмеченными точками только за счет выбора точек 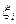 .
.
Составим сумму 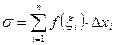 , которую назовем интегральной суммой. Эта сумма зависит от функции
, которую назовем интегральной суммой. Эта сумма зависит от функции 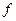 , от способа разбиения отрезка
, от способа разбиения отрезка  на части, а также от выбора точек
на части, а также от выбора точек 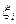 . Число
. Число 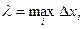 назовем параметром разбиения
назовем параметром разбиения 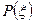 . Очевидно, что одно и то же число
. Очевидно, что одно и то же число 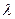 может являться параметром для бесконечного множества разбиений с отмеченными точками.
может являться параметром для бесконечного множества разбиений с отмеченными точками.
Определение 3. Число 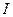 назовем определенным интегралом от функции
назовем определенным интегралом от функции 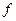 на отрезке
на отрезке  , если для любого
, если для любого 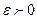 найдется
найдется 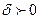 такое, что для любого разбиения
такое, что для любого разбиения 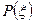 с отмеченными точками с параметром
с отмеченными точками с параметром 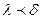 будет выполняться условие
будет выполняться условие 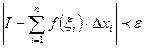 .
.
Обозначение: 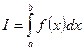 . При этом
. При этом 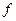 называют подинтегральной функцией;
называют подинтегральной функцией; 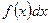 - подинтегральным выражением;
- подинтегральным выражением; 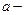 нижним пределом интегрирования;
нижним пределом интегрирования; 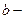 верхним пределом интегрирования.
верхним пределом интегрирования.
Теорема 2. Если функция 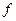 интегрируема на
интегрируема на  , то она ограничена на
, то она ограничена на  .
.
Свойства определенного интеграла:
1°. Если функция 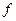 интегрируема на
интегрируема на  , то функция
, то функция 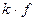 , где
, где 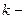 число, также будет интегрируемой на
число, также будет интегрируемой на  , причем
, причем 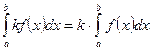 .
.
2°. Если функции 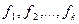 интегрируемы на
интегрируемы на  , то функция
, то функция 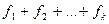 . Также будет интегрируемой на
. Также будет интегрируемой на  , причем
, причем 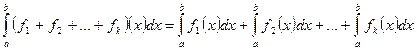
3°. Если функция 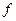 интегрируема на
интегрируема на  и
и 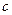 - некоторая внутренняя точка
- некоторая внутренняя точка  , то функция
, то функция 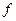 будет интегрируема на каждом из отрезков
будет интегрируема на каждом из отрезков 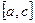 и
и 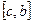 , причем
, причем 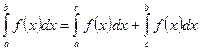 .
.
4°. Если функция 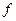 интегрируема на
интегрируема на  и
и 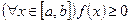 , то
, то 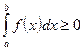 .
.
5°. Если функции 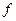 и
и 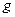 интегрируемы на
интегрируемы на  и
и 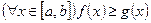 , то
, то 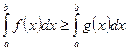 .
.
6°. Если функция 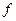 интегрируема на
интегрируема на  , то и функция
, то и функция 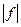 будет интегрируема на
будет интегрируема на  , причем
, причем 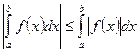 .
.
7°. Если функция 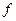 интегрируема на
интегрируема на  и
и 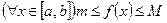 , то
, то 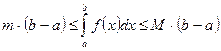 .
.
8°. Если функция 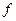 интегрируема на
интегрируема на  и
и 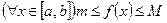 , то существует такое число
, то существует такое число 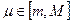 , для которого справедливо равенство
, для которого справедливо равенство 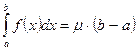 .
.
9° 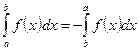 . В частности если
. В частности если 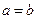 , то из последнего равенства следует, что
, то из последнего равенства следует, что 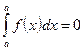 .
.
Теорема 3. Если функция 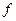 интегрируема на
интегрируема на  , то функция
, то функция 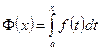 будет непрерывной на
будет непрерывной на  .
.
Теорема 4. Если функция 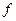 непрерывна на
непрерывна на  , то функция
, то функция 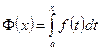 будет дифференцируемой на
будет дифференцируемой на  , причем
, причем 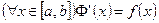 .
.
Формула Ньютона – Лейбница : 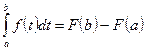 .
.
Теорема 5. Пусть функция 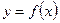 непрерывна на
непрерывна на  , а функция
, а функция 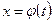 , определенная на
, определенная на 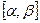 , обладает следующими свойствами:
, обладает следующими свойствами:
1) 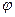 имеет непрерывную производную на
имеет непрерывную производную на 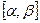 ;
;
2) 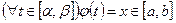 ;
;
3) 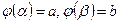 .
.
Тогда 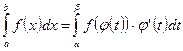 .
.
Теорема 6. Если функции 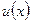 и
и 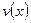 имеют на
имеют на  непрерывные производные функции, то справедлива формула
непрерывные производные функции, то справедлива формула 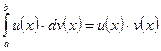 |
| 
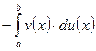 (формула интегрирования по частям в определенном интеграле).
(формула интегрирования по частям в определенном интеграле).
Вычисление площадей плоских фигур с помощью определенного интеграла.
