Параллелепипед с граничными условиями третьего рода
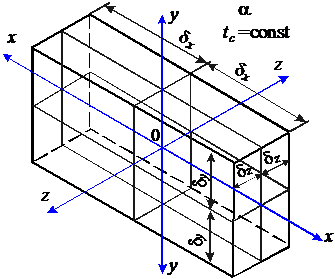 Рис. 28. Параллелепипед Рис. 28. Параллелепипед | Рассмотрим охлаждение параллелепипеда в среде с постоянной температурой и с постоянным коэффициентом теплоотдачи 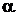 на всех гранях (рис. 28). В начальный момент времени температура во всех точках параллелепипеда одинакова и равна на всех гранях (рис. 28). В начальный момент времени температура во всех точках параллелепипеда одинакова и равна 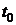 . Размеры параллелепипеда равны . Размеры параллелепипеда равны 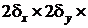 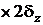 . Начало координат поместим в центр параллелепипеда. Уравнение теплопроводности имеет вид . Начало координат поместим в центр параллелепипеда. Уравнение теплопроводности имеет вид 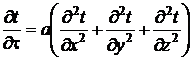 . . |
Параллелепипед можно рассматривать как тело, образованное пересечением трёх бесконечных пластин толщиной 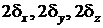 . В таком теле при принятых условиях температурное поле симметрично относительно центра параллелепипеда. Решение данной задачи может быть получено на основании теоремы перемножения решений. Решение представляется в виде
. В таком теле при принятых условиях температурное поле симметрично относительно центра параллелепипеда. Решение данной задачи может быть получено на основании теоремы перемножения решений. Решение представляется в виде
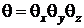 ,
,
где 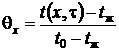 ;
; 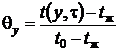 ;
; 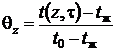 есть решения одномерных уравнений теплопроводности для трёх бесконечных пластин
есть решения одномерных уравнений теплопроводности для трёх бесконечных пластин 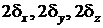 , а
, а
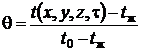 .
.
Цилиндр конечной длины
Цилиндр диаметром 2R и длиной 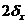 находится в среде с постоянной температурой в условиях, аналогичным рассмотренным для параллелепипеда. Цилиндр конечной длины можно рассматривать как тело, образованное пересечением бесконечного цилиндра диаметра 2R и бесконечной пластины толщиной
находится в среде с постоянной температурой в условиях, аналогичным рассмотренным для параллелепипеда. Цилиндр конечной длины можно рассматривать как тело, образованное пересечением бесконечного цилиндра диаметра 2R и бесконечной пластины толщиной 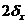 .
.
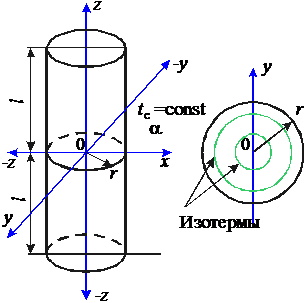 Рис. 29. Цилиндр конечной длины Рис. 29. Цилиндр конечной длины | Таким образом, применяя теорему перемножения решений, можно определить безразмерную относительную температуру в виде 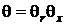 , где , где 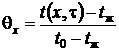 , , 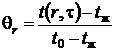 . Значение . Значение 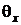 находится по формуле (5.10), а значение находится по формуле (5.10), а значение 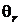 – по формуле (5.14). Средняя безразмерная температура находится по формуле – по формуле (5.14). Средняя безразмерная температура находится по формуле 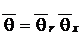 , где , где 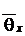 средняя безразмерная температура бесконечной пластины толщиной средняя безразмерная температура бесконечной пластины толщиной |
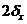 , а
, а 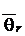 средняя безразмерная температура бесконечного цилиндра радиуса R.
средняя безразмерная температура бесконечного цилиндра радиуса R.
5.4. Регулярный режим охлаждения (нагревания) тел
Анализ решений для тел различной формы показывает, что они имеют одинаковую структуру – сумму бесконечного ряда, члены которого убывают по экспоненте. Этот ряд в обобщённом виде можно записать следующим образом.
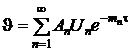 ,
, 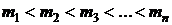 .
.
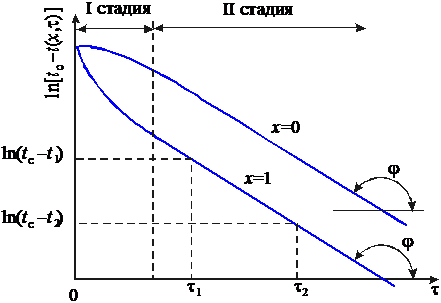 Рис. 30. К регулярному режиму охлаждения Рис. 30. К регулярному режиму охлаждения | Коэффициенты ряда 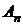 и и 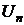 зависят от формы тела. При малых значениях времени зависят от формы тела. При малых значениях времени 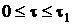 распределение температуры внутри тела и скорость изменения температуры в точках тела зависят от особенностей начального распределения температуры, т.е. от начальных условий. Этот период называется первой стадией процесса. С увеличением времени ряд быстро сходится распределение температуры внутри тела и скорость изменения температуры в точках тела зависят от особенностей начального распределения температуры, т.е. от начальных условий. Этот период называется первой стадией процесса. С увеличением времени ряд быстро сходится |
и, начиная с некоторого момента времени 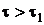 начальные условия уже не влияют на процесс охлаждения. Он полностью зависит от условий охлаждения на поверхности тела, теплофизических свойств, формы и размеров. Поле температур
начальные условия уже не влияют на процесс охлаждения. Он полностью зависит от условий охлаждения на поверхности тела, теплофизических свойств, формы и размеров. Поле температур
описывается первым членом ряда 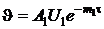 . Логарифмируя это выражение, получим
. Логарифмируя это выражение, получим 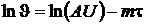 или
или
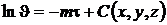 . (5.15)
. (5.15)
Т.е. логарифм избыточной температуры для всех точек тела линейно зависит от времени. Этот период называется второй стадией охлаждения – регулярным режимом. При длительном охлаждении, т.е. при 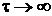 все точки тела принимают одинаковую температуру, равную
все точки тела принимают одинаковую температуру, равную 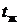 . Этот период соответствует стационарному режиму.
. Этот период соответствует стационарному режиму.
Если продифференцировать (5.15) по времени, получим
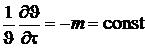 .
.
Величина m имеет размерность 1/сек и называется темпом охлаждения. В регулярном режиме темп охлаждения не зависит ни от времени, ни от координат и одинаков для всех точек тела.
