Решение задачи коши для дифференциального уравнения первого порядка или системы дифференциальных уравнений первого порядка

ПРАКТИЧЕСКАЯ РАБОТА № 2 (1)

Подвариант № 1

РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА ИЛИ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА

Цель работы

освоить методы Рунге-Кутта второго и четвертого порядка точности, применяемые для численного решения задачи Коши для дифференциального уравнения (или системы дифференциальных уравнений) первого порядка.

Постановка задачи

Рассматривается обыкновенное дифференциальное уравнение первого порядка, разрешенное относительно производной и имеющее вид:

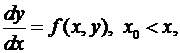(1)

с дополнительным начальным условием, заданным в точке :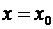

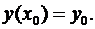(2)

Предполагается, что правая часть уравнения (1) функция 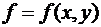такова, что гарантирует существование и единственность решения задачи Коши (1)-(2).

В том случае, если рассматривается не одно дифференциальное уравнение вида (1), а система обыкновенных дифференциальных уравнений первого порядка, разрешенных относительно производных неизвестных функций, то соответствующая задача Коши имеет вид (на примере двух дифференциальных уравнений):

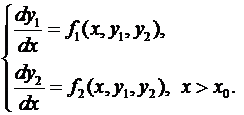(3)

Дополнительные (начальные) условия задаются в точке :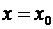

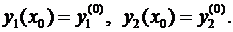(4)

Также предполагается, что правые части уравнений из (3) заданы так, что это гарантирует существование и единственность решения задачи Коши (3)-(4), но уже для системы обыкновенных дифференциальных уравнений первого порядка в форме, разрешенной относительно производных неизвестных функций.

Заметим, что к подобным задачам сводятся многие важные задачи, возникающие в механике (уравнения движения материальной точки), небесной механике, химической кинетике, гидродинамике и т.п.

Цели и задачи практической работы

1) Решить задачу Коши (1)-(2) (или (3)-(4)) наиболее известными и широко используемыми на практике методами Рунге-Кутта второго и четвертого порядка точности, аппроксимировав дифференциальную задачу соответствующей разностной схемой (на равномерной сетке); полученное конечно-разностное уравнение (или уравнения в случае системы), представляющее фактически некоторую рекуррентную формулу, просчитать численно;

2) Найти численное решение задачи и построить его график;

3) Найденное численное решение сравнить с точным решением дифференциального уравнения (подобрать специальные тесты, где аналитические решения находятся в классе элементарных функций, при проверке можно использовать ресурсы on-line системы http://www.wolframalpha.com или пакета Maple и т.п.).

Варианты заданий

Таблица 1.

Варианты задания правой части уравнения (1) и начального условия (2)

в случае одного дифференциального уравнения

Вариант		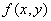	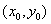Точное решение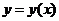

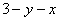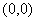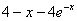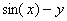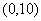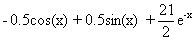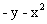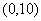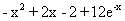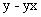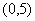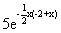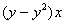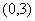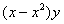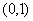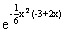Таблица 2.

Варианты задания правых частей системы (3) и начального условия (4)

в случае системы двух обыкновенных дифференциальных уравнений

Вариант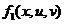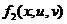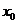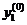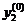
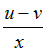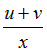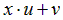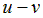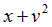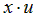					-1
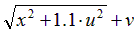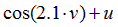				0.5
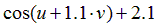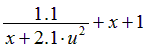					0.05
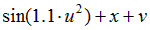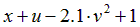					0.5
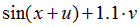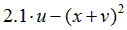				0.5
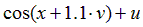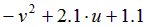				0.25
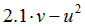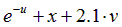					0.25
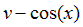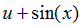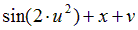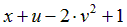					0.5
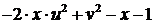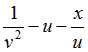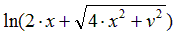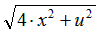				0.5
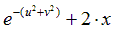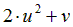				0.5
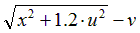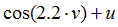				0.5
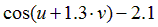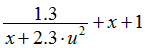					0.05
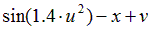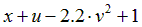					0.5
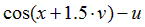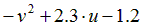				0.25
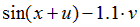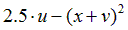				0.5
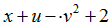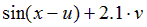				1.5
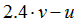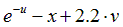					0.25

ПРАКТИЧЕСКАЯ РАБОТА № 2 (2)

Подвариант № 2

Цель работы

освоить метод прогонки решения краевой задачи для дифференциального уравнения второго порядка.

Постановка задачи

Рассматривается линейное дифференциальное уравнение второго порядка вида

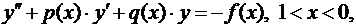(1)

с дополнительными условиями в граничных точках

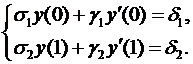(2)

Варианты заданий

1. ; ; .

2. ; ; .

3. ; ; .

4. ; ; .

5. ; ; .

6. ; ; .

7. ; ; .

8. ; ; 2 y(1.5) - 0.5.

9. ; ; .

10. ; 2 y(1.3) - ; .

11. ; ; .

12. ; ; y(0.7) +

13. ; ;

14. ; ; .

15. ; ; .

ПРАКТИЧЕСКАЯ РАБОТА № 2 (1)

Подвариант № 1

РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА ИЛИ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА

Цель работы

освоить методы Рунге-Кутта второго и четвертого порядка точности, применяемые для численного решения задачи Коши для дифференциального уравнения (или системы дифференциальных уравнений) первого порядка.

Постановка задачи

Рассматривается обыкновенное дифференциальное уравнение первого порядка, разрешенное относительно производной и имеющее вид:

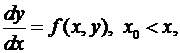(1)

с дополнительным начальным условием, заданным в точке :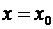

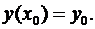(2)

Предполагается, что правая часть уравнения (1) функция 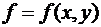такова, что гарантирует существование и единственность решения задачи Коши (1)-(2).

В том случае, если рассматривается не одно дифференциальное уравнение вида (1), а система обыкновенных дифференциальных уравнений первого порядка, разрешенных относительно производных неизвестных функций, то соответствующая задача Коши имеет вид (на примере двух дифференциальных уравнений):

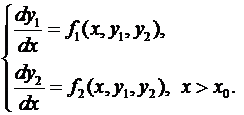(3)

Дополнительные (начальные) условия задаются в точке :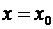

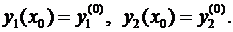(4)

Также предполагается, что правые части уравнений из (3) заданы так, что это гарантирует существование и единственность решения задачи Коши (3)-(4), но уже для системы обыкновенных дифференциальных уравнений первого порядка в форме, разрешенной относительно производных неизвестных функций.

Заметим, что к подобным задачам сводятся многие важные задачи, возникающие в механике (уравнения движения материальной точки), небесной механике, химической кинетике, гидродинамике и т.п.