Графическое дифференцирование

Если имеется график функции положения механизма, то вычисление производных – аналогов скорости и ускорения выполняется с использованием методов графического дифференцирования. Эти методы используют геометрический смысл производной функции одного аргумента (Рис. 22,а):

,

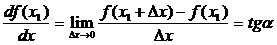т.е. производная функции, вычисленная при фиксированном значении аргумента, равна тангенсу угла, образованного осью абсцисс и касательной τ, проведенной к графику функции в точке вычисления производной.

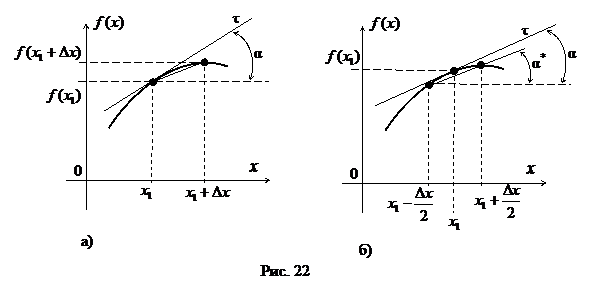Ясно, что значения производной функции в заданных точках можно найти геометрически, проводя касательные к графику функции. При этом нет необходимости измерять углы наклона касательных и вычислять тангенсы, так как при постоянном значении прилежащего к углу α катета, значения производной в каждой точке графика будут пропорциональны длине противолежащего катета. В теории механизмов для графического вычисления аналогов скорости и ускорения применяются метод касательных и метод хорд.

Метод касательных предполагает выполнение следующих геометрических операций.

· В пронумерованных точках графика функции проводятся касательные.

· Полученные касательные параллельно переносятся и проводятся через одну и ту же заранее выбранную точку на оси абсцисс, лежащую на расстоянии k слева от оси ординат.

· Измеряется расстояние от начала отсчета до точки пересечения касательной с осью ординат, которое пропорционально значению производной.

Масштабы первой и второй производных вычисляются по формулам:

, .

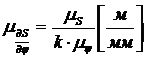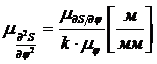где расстояние k - в миллиметрах. Несмотря на то, что метод касательных теоретически позволяет вычислить производную абсолютно точно, погрешности геометрических построений и измерений практически позволяют выполнить лишь приближенные вычисления. Наибольший вес здесь имеют ошибки при проведении касательных, особенно в тех случаях, когда расчет выполняется без применения средств автоматизации геометрических построений (вручную).

Метод хорд основан на идее замены касательной, проведенной в точке графика посередине малого интервала, хордой, стягивающей точки графика на концах интервала (рис. 22,б). Ясно, что если функция f(x) гладкая и в пределах интервала Δx ее производная не изменяется очень быстро, то 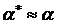и замена касательной τ на хорду при графическом дифференцировании вполне оправдана, так как построение хорды вручную существенно более точное, чем построение касательной.

Аналог ускорения определяется в том же порядке, путем графического дифференцирования аналога скорости. Масштабы производных вычисляются по тем же формулам, что и в методе касательных. Следует отметить, что при выполнении ответственного расчета вручную, повторное графическое дифференцирование из-за больших погрешностей не допускается.

Контрольные вопросы

1. Что называют планом положений механизма?

2. Какое положение механизма обычно принимается за начальное (нулевое) при построении плана положений?

3. Как при помощи плана положений построить график функции положения механизма?

4. В каком виде определяется функция положения механизма при использовании аналитического метода?

5. Во всех ли случаях целесообразно, выполняя кинематический анализ механизма, использовать аналитический метод? Обоснуйте свой ответ.

6. Какое утверждение положено в основу методов графического дифференцирования функции положения?

7. Как выполняется графическое дифференцирование методом касательных?

8. В каком случае, вместо метода касательных, удобнее применить метод хорд?

1.16. Метод векторных планов

Некоторые физические величины, характеризующие состояние исследуемой системы, могут быть математически представлены в виде направленных отрезков (векторов). Например, векторными величинами являются скорости и ускорения точек механической системы, силы, приложенные к системе, переменные ток и напряжение в электрической цепи и т.п. В подобных случаях процессы, протекающие в системе, описываются векторными уравнениями. Если векторы, входящие в уравнения, находятся в одной и той же плоскости, то уравнения могут быть решены путем геометрических построений векторов на плоскости в заранее принятом масштабе. В этом заключается идея метода векторных планов. Когда требуется вычислить скорости и ускорения звеньев плоского механизма в каких-либо его положениях, метод векторных планов является удобным и часто применяется на практике.

Как известно из теоретической механики, скорость и ускорение любой точки твердого тела, совершающего плоское движение (Рис. 23), могут быть найдены с помощью векторных уравнений:

, ,

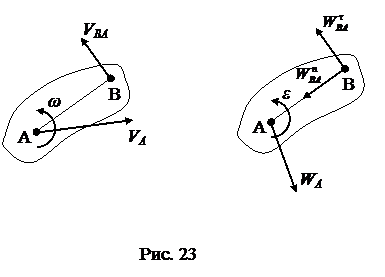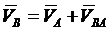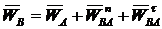где 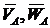- векторы абсолютных скорости и ускорения точки А тела, 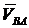- вектор скорости точки B относительно точки A, 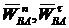- векторы нормального и тангенциального (касательного) ускорений точки B относительно точки A. Модули векторов 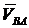, 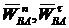вычисляются по формулам

, , ,

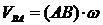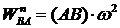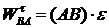где ω, ε – угловые скорость и ускорение тела.

Векторные планы, соответствующие векторным уравнениям скоростей и ускорений, представлены на рис. 24.

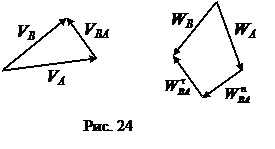Таким образом, выполнив графически сложение векторов и измерив на планах отрезки, соответствующие скорости 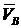и ускорению 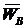, получаем информацию о направлениях и величинах векторов 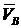и .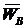

· Векторный план, показывающий распределение скоростей точек звеньев исследуемого механизма в заданном его положении, называется планом скоростей механизма.

· Векторный план, показывающий распределение ускорений точек звеньев исследуемого механизма в заданном его положении, называется планом ускорений механизма.

Контрольные вопросы

1. В чем состоит идея метода векторных планов?

2. Почему метод векторных планов целесообразно применять в кинематическом анализе плоского механизма?

3. По каким векторным уравнениям определяются скорость и ускорение произвольной точки звена плоского механизма?

4. Что называют планом скоростей механизма? Планом ускорений?