Свободные колебания одномассовой системы

Частота и период свободных колебаний являются ос­новными динамическими характеристиками системы и ис­пользуются во всех динамических расчетах.

Одномассовая модель представляет собой точечную массу т, связанную с основанием упругой связью, имеющей ко­эффициент жесткости с (см. рис. 5.1, б, в). Положение мас­сы в процессе колебаний характеризуется координатойу, которая отсчитывается от ее начального положения. Если переместить массу на некоторое расстояние и отпустить, то масса будет совершать свободные колебания. Исполь­зуя принцип Д’Аламбера (кинетостатики), составим урав­нение движения в форме условия равновесия массы т с уче­том сил инерции. Оно запишется следующим образом:

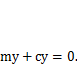(5.3)

Преобразуем это уравнение к виду 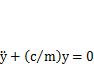и, обозначив 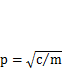, представим как

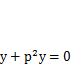(5.4)

Полученное выражение является обыкновенным однородным дифференциальным уравнением с постоянными коэффициентами. Для нахождения общего решения соста­вим характеристическое уравнение

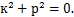
Оно имеет два сопряженных мнимых корня 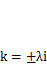, следовательно, решения уравнения имеют вид

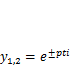
Общим решением однородного уравнения является сум­ма двух линейно независимых частных решений, в качестве которых используем две комбинации полученных решений:

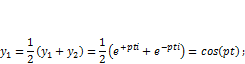
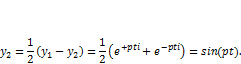
(5.5)

следовательно, общее решение однородного уравнения можно записать с использованием произвольных постоян­ных как

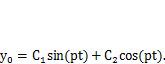
Отсюда видно, что величина р является круговой частотой свободных колебаний одномассовой системы. Она количественно равна числу колебаний за время 2п секунд. Соответственно период колебаний составляет 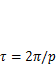, а частота 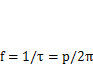. Таким образом, частота свободных колебаний одномассовой системы

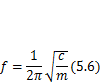
Жесткость конструкции 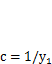, где — упругий прогиб от единичной силы, приложенной в точке расположе­ния массы т.

Пример 5.1. Проверка динамических характеристик консоли, несущей привод механизма передвижения мостового крана. Привод,включающийдвигатель, муфту, редуктор,

промежуточный вал с зубчатыми муфтами и его основание, имеет суммарную массу т = 180 кг. Двигатель вращается со скоростью 920 об/мин. Момент на тихоходном валу редуктора 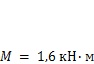. Центр тяжести привода находится на расстоянии L= 1 м от корня консоли. Консоль состоит из двух гнутых швеллеров № 100x80x4 из стали СтЗ, с моментом инерции 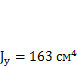(рис. 5.3, а).

Выполним расчет консоли на прочность по максималь­ным напряжениям в корне от веса привода 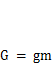и реак­тивного момента М_г, которые найдем по известной фор­муле (рис. 5.3, б):

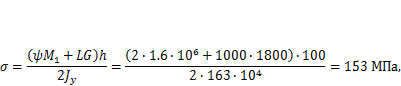
где — динамический коэффициент приложения мо­мента (п. 5.4.1).

Условие прочности консоли выполнено: .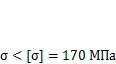

Частота свободных колебаний консоли с приводом оп­ределяется по динамической модели (рис. 5.3, в), для ко­торой коэффициент жесткости (8.2)

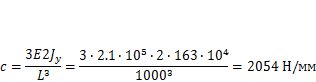
Пренебрегая приведенной массой швеллеров, найдем ча­стоту колебаний (5.6)

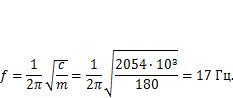
Возмущающая сила, которую может создавать электро­двигатель при наличии неуравновешенности ротора, будет действовать с частотой 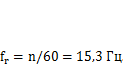Таким образом, частота свободных колебаний отличается от частоты воз­мущающей силы примерно на 10 %. Такое положение может вызвать чрезвычайно большие колебания конструкции и привести к возникновению усталостного поврежденияв сварном соединении швеллеров с основанием. Для реше­ния этой проблемы необходимо повысить жесткость консоли.