Метод перемещений для расчета статически неопределимых систем

Метод перемещений в определенном смысле противопо­ложен методу сил. При использовании метода сил отбра­сываются лишние связи и из кинематических условий на­ходятся действующие в них усилия. В методе перемеще­ний вводятся дополнительные «управляемые» связи в уз­лах конструкции и из условий равенства нулю реакций в этих фиктивных связях вычисляются фактические зна­чения перемещений. По найденным значениям перемеще­ний узлов можно определить внутренние усилия в любомэлементе конструкции. Метод перемещений удобен для ком­пьютерной реализации, так как в нем, в отличие от мето­да сил, основная система задается единственным образом.

Рассмотрим алгоритм расчета этим методом.

1. Производится анализ заданной системы в целях оп­ределения степени ее кинематической неопределимости, т. е. количества неизвестных линейных и угловых переме­щений.

Для определения линейных перемещений в заданной си­стеме все жесткие связи между стержнями и между стерж­нями и основанием заменяют шарнирами, после чего на­ходят количество опорных стержней, которые надо уста­новить, чтобы система стала геометрически неизменяемой (рис. 4.8, а—в). Добавленные опорные стержни (обозначе­ны двойной линией) показывают расположение и количе­ство неизвестных линейных перемещений.

Количество угловых неизвестных перемещений равно ко­личеству жестких узлов заданной системы, в которых соеди­няются два или более стержней. Степень кинематической не­определимости vравна суммарному количеству линейных и угловых неизвестных перемещений. Система на рис. 4.8 три раза кинематически неопределима 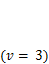. Следует отметить, что степень кинематической неопределимости никак не свя­зана со степенью статической неопределимости. Так, та же система один раз статически неопределима.

2.

Основная система получается из заданной путем вве­дения дополнительных, фиктивных (не существующих в реальности) связей ( штук). Во все жесткие узлы (жесткое соединение двух и более стержней) вводят заделки, пре­пятствующие угловым перемещениям, а в тех местах, где обнаружены неизвестные линейные перемещения, разме­щают опорные стержни (рис. 4.8, г). Особенность фиктив­ных заделок такова, что каждая из них блокирует только одно перемещение — поворот узла — и не препятствует линейным перемещениям. Кроме того, каждой из фиктив­ных связей при необходимости можно задать произволь­ное перемещение по ее направлению, т. е. повернуть за­делку на какой-то угол или сместить опорный стержень в его же направлении.

3. Далее необходимо сформулировать условия, при вы­полнении которых основная система будет полностью иден­тична заданной. Это произойдет в том случае, если все фиктивные связи получат перемещения, равные переме­щениям этих узлов в заданной системе под действием ре­альных нагрузок. При этом реакции в этих связях будут равны нулю: 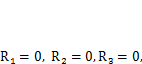так как они не отклоня­ют систему от ее равновесного состояния. Полагая, что рассчитываемые системы являются линейными (п. 2.1.1), и применяя принцип суперпозиций, реакции, возникающие в каждой фиктивной связи, можем представить как сумму реакций от перемещения всех фиктивных связей и от внеш­ней нагрузки, т. е.:

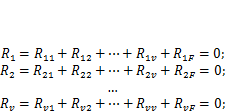
Здесь обозначено: — реакция, возникающая в k-й связи при перемещении j-й связи в ее «естественное» положе­ние, т. е. соответствующее перемещению в заданной систе­ме (k= 1, 2,... и, у = 1, 2,..., и).Поскольку рассматриваемые системы линейны, эта реакция пропорциональна переме­щению j-й связи, т. 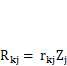е. ,где — фактическое (искомое) перемещение у-й связи в заданной системе; — коэффициент жесткости, численно равный усилию, кото­рое возникает в k-й связи приеденичном перемещении j-й связи, он имеет размерность 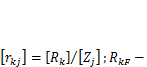свободный член уравнения, равный реакции, возникающей в k-й связи от внешней нагрузки.С учетом введенных обо­значений можем записать систему канонических уравне­ний метода перемещений в следующем виде:

(4.14)

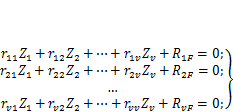
Количество уравнений равно степени кинематической неопределимости системы. Для схемы на рис. 4.8 следует записать три уравнения:

(4.15)

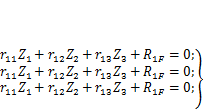
Далее необходимо определить коэффициенты этих урав­нений и свободные члены .

4. Значения коэффициентов канонических уравнений вы­числяют статическим методом. Для этого, используя гото­вые решения (табл. 4.1), строят эпюры изгибающих мо­ментов для vсостояний, в каждом из которых задается единичное смещение одной из фиктивных связей (рис. 4.8, д—ж) и от внешней нагрузки (рис. 4.8, з). После чего тре­буемые значения коэффициентов и свободных членов получаются как реакции в соответствующих связях.

Рассмотрим методику определения коэффициентов ка­нонических уравнений статическим методом на примере системы, представленной на рис. 4.8.

В состоянии 1 фиктивная связь 1 смещается по своему направлению на 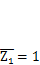. Горизонтальный ригель смещает­ся без изгиба. Изгиб вертикального стержня приводит к возникновению горизонтальной реакции в связи 1 (табл. 4.1, п. 5):

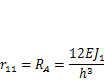
и моментной реакции в связи 2, которая находится из ус­ловия равновесия узла (рис. 4.8, и, табл. 4.1, п. 5),

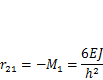
Реакция , возникающая при повороте заделки, равна сумме изгибающих моментов (М₂) в сечениях стержней, примыкающих к узлу (рис. 4.8, е, к, М’₂, М₂, М₂). Значе­ния этих моментов находятся по табл. 4.1 (п. 1 и 4), на­правление действия момента, приложенного к узлу,

определяется по расположению растянутого волокна, ко­торое указывает эпюра. В результате получится

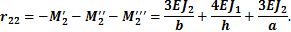
Остальные коэффициенты вычисляются по формулам табл. 4.1:

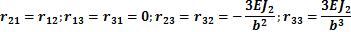
Свободные члены канонических уравнений равны зна­чениям реакций в связях 1, 2 и 3 от внешней нагрузки F. Как видно из схем на рис. 4.8, з,

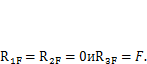
5. После подстановки всех коэффициентов в систему (4.14) вычисляются значения перемещений всех фиктив­ных связей .

6. Результирующая эпюра изгибающих моментов стро­ится как сумма эпюр (рис. 4.8, л)

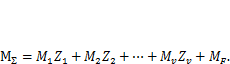
Проконтролировать правильность решения можно пу­тем проверки условий равновесия узлов в результирующей эпюре моментов.

Расчет пластин и оболочек