Принцип возможных перемещений

Как известно из курса теоретической механики, усло­вие равновесия объекта может иметь силовую или энерге­тическую формулировку. Первый вариант представляет со­бой условие равенства нулю главного вектора и главного момента всех сил и реакций, действующих на тело. Вто­рой подход (вариационный), называемый принципом воз­можных перемещений, оказался весьма полезен для реше­ния ряда задач строительной механики.

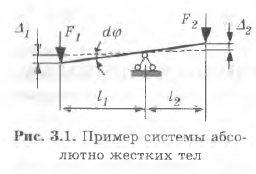Для системы абсолютно жесткихтел принцип возможных перемещений формулируется так: если система абсолютно жестких тел находится в равнове­сии, то сумма работ всех внешних сил на любом возможном бесконечно малом перемещении равна нулю. Возмож­ным (или виртуальным) называют перемещение, которое не нарушает кинематические связи и сплошность тел. Для системы на рис. 3.1 возможным является только поворот стержня относительно опоры. При повороте на произволь­ный малый угол силы и совершают работу 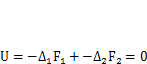Согласно принципу возможных переме­щений, если система находит­ся в равновесии, то должно быть 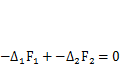. Подставляя сюда геометрические соотношения 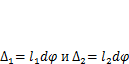получим условие равнове­сия в силовой формулировке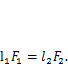

Принцип возможных перемещений для упругихтел формулируется следующим образом: если система упру­гих тел находится в равновесии, то сумма работ всех внешних и внутренних сил на любом возможном бесконечно малом перемещении равна нулю. В основе этого прин­ципа лежит понятие о полной энергии упругой деформи­рованной системы П. Если нагружение конструкции про­исходит статически, то эта энергия равна работе, совер­шаемой внешними Uи внутренними Wсилами при переводе системы из деформированного состояния в исходное:

П= U + W.

При указанном переводе внешние силы не меняют свое­го значения и совершают отрицательную работу U= -F . Внутренние силы при этом уменьшаются до нуля и совершают положительную работу, так как это силы сцепления частиц материала и направлены в сторону, противополож­ную внешней нагрузки:

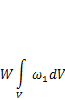
где 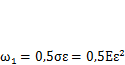— удельная потенциальная энергия упругой деформации; V — объем тела. Для линейной системы , где 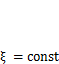. Согласно теореме Лагранжа—Дирихле состоянию устойчивого равновесия соответствует мини­мум полной потенциальной энергии упругой системы, т. е.

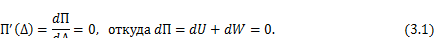
Последнее равенство полностью соответствует формули­ровке принципа возможных перемещений. Приращения энергий dUи dWмогут быть вычислены на любых возможных перемещениях (отклонениях) упругой системы от со­стояния равновесия. Для расчета конструкций, удовлетво­ряющих требованиям линейности, бесконечно малое возможное перемещение d можно заменить весьма малым конеч­ным перемещением , в качестве которого может быть выбрано любое деформированное состояние конструкции, созданное произвольно выбранной системой сил. С учетом этого полученное условие равновесия следует записать как

(3.2)

Далее рассмотрены методики вычисления работы внешних Uи внутренних Wсил.

Работа внешних сил

Рассмотрим методику вычисления работы внешних сил на действительном и возможном перемещении. Стержне­вая система загружена силами и (рис. 3.2, а), которые действуют одновременно, и в любой момент времени отношение 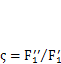остается постоянным. Если считать обобщенной силой, то по значению в любой момент времени можно вычислить все остальные нагрузки (в данном случае 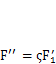). Штриховой линией показано действительное упругое перемещение, возникающее от этих сил. Обозначим это состояние индексом 1. Перемещение точек приложения сил и в направлении этих сил в состоянии 1 обозначим и .

В процессе нагружения линейной системы силами и растут силы и пропорционально им растут перемещения и (рис. 3.2, в). Действительная работа сил и на создаваемых ими перемещениях равна сумме площадей графиков 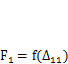, т. е. 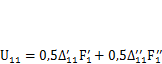. Записав это выражение как 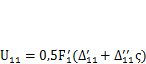, получим произведение обобщенной силы на обобщенное пе­ремещение 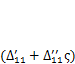. В этой форме можно представит

работу сил при любом нагружении, если все нагрузки изменяются синхронно, т. е. отношение их значений остается постоянным.

Далее рассмотрим работу внешних сил на возможном перемещении. В качестве возможного перемещения при­мем, например, деформированное состояние системы, воз­никающее в результате приложения в некоторой точке силы 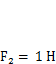(рис. 3.2, б). Это состояние, соответству­ющее дополнительному перемещению точек приложения сил и на расстояние и , обозначим 2. Силы и , не меняя своего значения, совершают виртуальную работу на перемещениях и (Рис. 3.2, в):

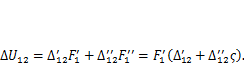
Как видно, в обозначении перемещения первый индекс показывает состояние, в котором заданы точки и направле­ния этих перемещений. Второй индекс показывает состоя­ние, в котором действуют силы, вызывающие это переме­щение.

Работа единичной силы F₂на действительном перемещении

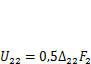
Если же рассматривать состояние 1 в качестве возмож­ного перемещения для силы F₂,то ее виртуальная работа на перемещении

.

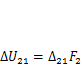Работа внутренних сил

Найдем работу внутренних сил состояния 1, т. е. от сил и , на виртуальных перемещениях состояния 2, т. е. возникших в результате приложения нагрузки F₂. Для этого выделим элемент стержня длиной dx(рис. 3.2 и 3.3, а). Поскольку рассматриваемая система плоская, то в сечениях элемента действуют только две силы Sи Q_zи изгибающий момент Му Эти усилия для вырезанного элемента являются внешними. Внутренние усилия — это усилия сцепления, обеспечивающие прочность материала. Они равны внешним по значению, но направлены в сторону, противоположную деформации, поэтому их работа при нагружении отрицательна (рис. 3.3, б—г, показаны серым цветом). Последовательно вычислим работу, совершаемую каждым силовым фактором.

Работа продольных сил 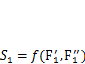на перемещении 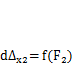, которое создают силы S₂, возникшие в результате приложения нагрузки F₂(рис. 3.2, б, 3.3, б),

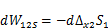
Удлинение стержня длиной dxнайдем по известной формуле [9]

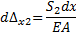
где A — площадь сечения стержня. Подставив это выра­жение в предыдущую формулу, находим

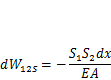
Аналогичным образом определим работу, которую со­вершает изгибающий момент на угловом перемещении ,создаваемом моментом (рис. 3.3, в):

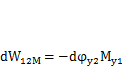
Угол поворота найдем как [9]

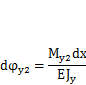
где J— момент инерции сечения стержня относительно оси у. После подстановки получим

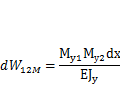
Найдем работу поперечной силы на перемещении (рис. 3.3, г). Касательные напряжения и сдвиги от перерезывающей силы Q_zраспределены по сечению стержня не линейно (в отличие от нормальных напряжений и удлинений в предыдущих случаях нагружения). Поэтому для определения работы сдвига приходится рассматривать работу, совершаемую касательными напряжениями в сло­ях стержня.

Касательные напряжения от силы Q_z, которые действу­ют в слое, лежащем на расстоянии zот нейтральной оси (рис. 3.3, д), вычисляются по формуле Журавского [9]

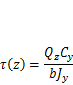
где Су — статический момент части площади сечения, лежащей выше этого слоя, взятый относительно оси у; b— ширина сечения на уровне рассматриваемого слоя. Эти напряже­ния создают сдвиг слоя на угол, который согласно закону Гука определяется как 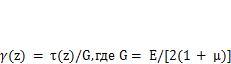— модуль сдвига. В результате этого торец слоя смещается на

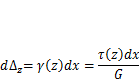
Суммарная работа касательных напряжений первого со­стояния , действующих на торце этого слоя, на пере­мещениях второго состояния 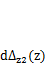вычисляется путем интегрирования произведения 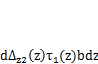поплощади сечения

.

После подстановки сюда выражений для и получим

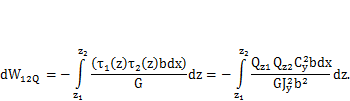
Вынесем из под интеграла величины, не зависящие от z, умножим и разделим это выражение наА, получим

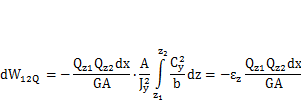
Здесь введен безразмерный коэффициент ,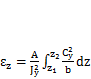

зависящий только от конфигурации и соотношения разме­ров сечений. Для прямоугольника = 1,2, для двутавро­вых и коробчатых сечений 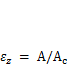(А_с — площадь сече­ния стенки или в коробчатом сечении — двух стенок).

Поскольку работа каждого из рассмотренных компонен­тов нагружения (S, Q, М) на перемещениях, вызываемых другими компонентами, равна нулю, то суммарная работа всех внутренних сил для рассмотренного элемента стержня длиной dx

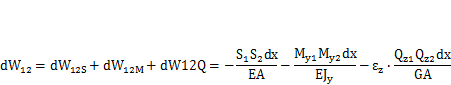
(3.3)

Суммарная работа внутренних сил состояния 1 на пере­мещениях состояния 2 для плоской стержневой системы получается путем интегрирования полученного выражения по участкам длиной 1_Ц, в пределах которых эпюры явля­ются интегрируемыми функциями, и суммирования по всем участкам:

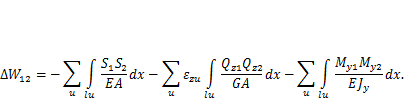
В сечении элемента пространственной стержневой сис­темы действуют шесть внутренних усилий (S, Q, Q_z, М_х, Му, М₂), поэтому для нее выражение суммарной работы внутренних сил будет иметь вид,

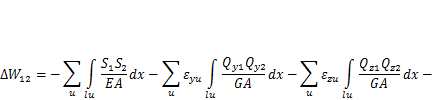
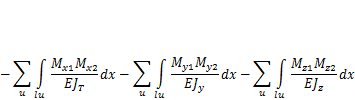
(3.4)

Здесь M_x — крутящий момент в стержне; J_T— момент инерции стержня при свободном кручении (геометрическая жесткость на кручение). В подынтегральном выражении опущены индексы «и».

В формулах (3.3) и (3.4) S_vQ_yVQ_zl, М_х1, М_у1, М_г1обозначают аналитические выражения эпюр внутренних усилий от действия сил F{и F{,aS₂, Q_y2, Q_z2, М_х2, М_у2, М_г2 — описания эпюр внутренних усилий от силы F₂.

Теоремы об упругих системах

Структура формул (3.3) и (3.4) показывает, что они «сим­метричны» относительно состояний 1 и 2, т. е. работа внут­ренних сил состояния 1 на перемещениях состояния 2 равна работе внутренних сил состояния 2 на перемещениях со­стояния 1 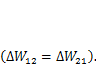Но согласно (3.2)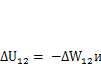

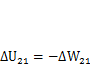, следовательно, если равны работы внутрен­них сил, то равны и работы внешних сил 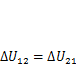-Это утверждение носит название теоремы о взаимности ра­бот (теорема Бетти, 1872 г.).

Для стержневой системы, загруженной силой F₁(рис. 3.4, а), возьмем в качестве возможного перемещения деформированное состояние, возникшее при загружении ее силой F₂(рис. 3.4, б). Для этой системы согласно теоре­ме Бетти 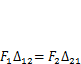1- Если же положить 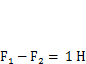, то получим

(3.5)

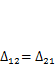
Эта формула выражает теорему Максвелла (1864 г.) о взаимности перемещений: перемещение точки приложе­ния первой единичной силы по ее направлению, вызван­ное действием второй единичной силы, равно перемеще­нию точки приложения второй единичной силы по своему направлению, вызванному действием первой единичной силы. Эту теорему можно применить и к системе на рис. 3.2. Если задать = 1 Н (п. 3.1.2), то получим ра­венство обобщенных перемещений .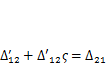

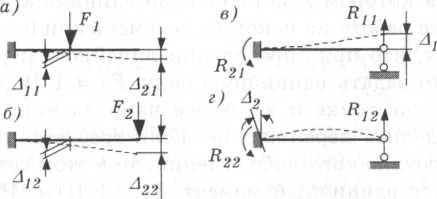Рис. 3.4. Пример применения теорем об упру­гих системах

Рассмотрим статически неопределимую систему с опо­рами, которым можно задавать требуемое перемещение, принимаемое как возможное (рис. 3.4, в, г). В первом со­стоянии сместим опору 1 на а во втором — зададим поворот заделки на угол - При этом возникнут реакции в первом состоянии и , а во втором — i 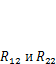. Согласно теореме о взаимности работ, запишем 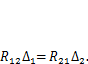Если задать 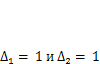(здесь размерность [ ] = м, а величина — безразмерная), то получим

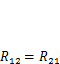(3.6)

Это равенство численное, так как размерность реакции [ ] = Н, a [ ] = Н-м. Таким образом, реакция R₁₂в неподвижной связи 1, возникающая при перемещении связи 2 на единицу, численно равна реакции , возника­ющей в связи 2 при единичном смещении связи 1. Это утверждение называется теоремой о взаимности реакций.

Теоремы, изложенные в данном разделе, используются для аналитического расчета статически неопределимых си­стем.

Определение перемещений

Общая формула перемещений

Для вычисления перемещений, возникающих в стерж­невой системе под действием заданной нагрузки (состоя­ние 1), следует сформировать вспомогательное состояние системы, в котором действует одно единичное усилие, совершающее работу на искомом перемещении (состояние 2). Это значит, что при определении линейного перемещения необходимо задать единичную силу F₂= 1 Н, приложен­ную в той же точке и в том же направлении, в котором надо определить перемещение. Если требуется определить угол поворота какого-либо сечения, то в этом сечении прикладывается единичный момент F₂ = 1 Н • м. После этого составляется уравнение энергий (3.2), в котором состояние 2 принимается за основное, а деформированное

состояние 1 рассматривается как виртуальное перемещение. Из этого уравнения и вычисляется искомое перемещение.

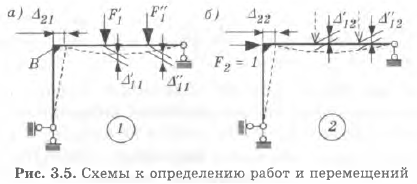
Найдем горизонтальное перемещение точкиВ для си­стемы на рис. 3.5, а. Для того чтобы в уравнение работ (3.2) попало искомое перемещение Д₂₁, возьмем в качестве основного состояния перемещение системы под действием единичной силы F₂- 1 Н (состояние 2, рис. 3.5, б). Возможным перемещением будем считать действительное де­формированное состояние конструкции (рис. 3.5, а).

Работу внешних сил состояния 2 на перемещениях со­стояния 1 найдем как Согласно (3.2),

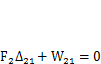
следовательно, искомое перемещение

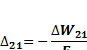
Поскольку 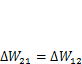(п. 3.1.4), работа внутренних сил состояния 2 на перемещениях состояния 1 вычисляется по формуле (3.3) или (3.4). Подставив в (3.7) выражение (3.3) дляработы внутренних сил плоской стержневой системы, найдем

Для дальнейшего использования этого выражения целесо­образно ввести понятие единичных эпюр внутренних сило­вых факторов, т.е. из которых первые две безразмерные, а размерность . В результате получится

В эти интегралы следует подставить выражения для эпюр распределениясоответствующих внутренних усилий от действующей нагрузки и и от силы F₂ = 1. Полу­ченное выражение называют формулой Мора (1881 г.).

При расчете пространственных стержневых систем для вычисления суммарной работы внутренних сил следует использовать формулу (3.4), тогда получится

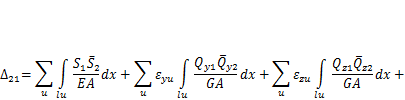
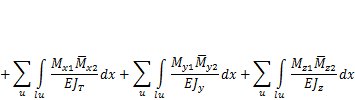
(3.9)

Вполне очевидно, что в интегралы подставляются выра­жения для эпюр внутренних усилий S, Q_y, Q_z, М_х, М_у, М_ги значения геометрических характеристик сечений A, J_т, Jу,J, для соответствующего n-го участка. Для сокращения записи в обозначениях этих величин индекс «и» опущен.

3.2.2. Частные случаи определения перемещений

Формула (3.8) используется в общем случае плоской стержневой системы, однако в ряде случаев ее можно существенно упростить. Рассмотрим частные случаи ее реализации.

1. Если деформациями от продольных сил можно пренебречь, что характерно для балочных систем, то формула(3.8) будет записана как

2. Если плоская система состоит только из изгибаемых тонкостенных балок с отношением l/h> 5 для консолей или l/h> 10 для пролетов (I и h— длина балки и высота сече­ния), то, как правило, энергия деформаций изгиба суще­ственно превышает энергию деформаций от продольных и поперечных сил, поэтому их можно не учитывать в расче­те перемещений. Тогда формула (3.8) примет вид

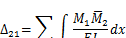
3. Для ферм, стержни которых при узловом нагруже­нии испытывают в основном продольные усилия, можно считать М = 0 и Q= 0. Тогда перемещение узла вычисля­ется по формуле

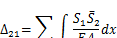
Интегрирование производится по длине каждого стерж­ня, а суммирование — по всем стержням. Имея в виду, что усилие S_uв и-м стержне и площадь сечения не изменяются по его длине, можем упростить данное выражение:

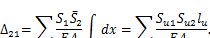
(3.12)

При всей видимой простоте этой формулы аналитиче­ский расчет перемещений в фермах весьма трудоемок, так как требует определения усилий во всех стержнях фермы от действующей нагрузки ( ) и от единичной силы ( ), приложенной в точке, перемещение которой необходимо найти.

3.2.3. Методика и примеры определения перемещений

Рассмотрим вычисление интеграла Мора методом А. Н. Верещагина (1925 г.). Интеграл Мора имеет вид 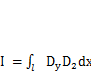(3.8), где в качестве D₁, D₂могут фигурировать эпюры изгибающих моментов, продольных или поперечных сил. Как минимум одна из эпюр ( ) в подынтегральном выражении линей­ная или кусочно-линейная, так как построена от единичной нагрузки. Поэтому для

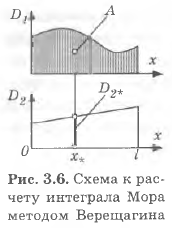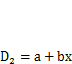решения интеграла можно применить следующий прием. Поло­жим, что на рассматриваемом участ­ке длиной I первая эпюра D₁произ­вольной формы, а вторая — линейная: (рис. 3.6). Подставив это в интеграл Мора, найдем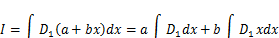

Первый изинтегралов численно равен площади подграфиком (на рис. 3.6 заштрихована), а второй — статическому моменту этой площади относительно оси . Статический момент может быть записан как 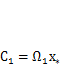, где — координата положения центра тяжести площади (точка А). С учетом сказанного получим

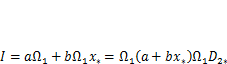(3.13)

Правило Верещагина формулируется следующим образом: если на участке хотя бы одна из эпюр линейна, то интеграл Мора вычисляется как произведение площади произволь

ной эпюры на ординату линейной эпюры, распо­ложенную под центром тяжести этой площади. Если обе эпюры расположены с одной стороны оси, то произведе­ние положительно, если с разных сторон, то — отрица­тельно. Этот метод может быть применен для вычисления любого из интегралов, входящих в выражения (3.8) и (3.9).

При расчете конструкций в среде Mathcadнет необхо­димости пользоваться правилом Верещагина, так как мож­но вычислять интеграл путем численного интегрирования.

Пример 3.1 (рис. 3.7, а). Балка загружена двумя сим­метрично расположенными силами . Найти перемеще­ния точек приложения сил .

1. Построим эпюру изгиба­ющих моментов М₁ от сил F₁. Опорные реакции 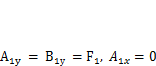Максимальный изгибающий момент под силой

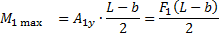
2. Поскольку система симметрична, то прогибы под силами будут одинаковы. В качестве вспомогательного состо­яния возьмем загружение бал­ки двумя единичными силами F₂= 1 Н, приложенными в тех же точках, что и силы F₁

(рис. 3.7, б). Эпюра изгибающих моментов для данного нагружения аналогична предыдущей, и максимальный изгибающий момент М_2тах=0,5(L-b).

3. Нагружение системы двумя силами второго состоя­ния характеризуется обобщенной силой F₂ и обобщенным перемещением 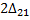, которые создают работу внешних сил на перемещении состояния 1, равную 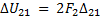. Вычислим перемещение по формуле (3.11). Перемножая эпю­ры по участкам по правилу Верещагина, найдем

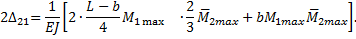
После подстановки значений 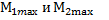получим

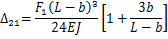
Пример 3.2. Найти горизонтальное перемещение подвижной опоры П-образной рамы, загруженной силой F_x(рис. 3.8, а).

1. Построим эпюру изгибающих моментов от силы F₁Опорные реакции 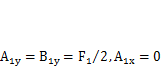. Максималь­ный изгибающий момент под силой F₁

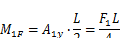
2. В качестве вспомогательного состояния возьмем загружение балки единичной горизонтальной силой F₂, при­ложенной в точкеВ (рис. 3.8, б). Строим эпюру изгиба­ющих моментов для этого случая нагружения. Опорные реакции А_2у = В_2у = 0, А_2х = 1. Максимальный изгибающий момент .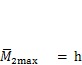

3. Вычисляем перемещение по формуле (3.11). На вер­тикальных участках произведение равно нулю. На гори­зонтальном участке эпюра М₁ не линейна, а эпюра линейна. Перемножая эпюры методом Верещагина, полу­чим

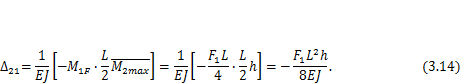
Произведение отрицательно, так как эпюры лежат по разные стороны. Полученное отрицательное значение перемещения свидетельствует о том, что фактическое его на­правление противоположно направлению единичной силы.

Пример 3.3 (рис. 3.9). Найти угол поворота сечения двухопорной балки под силой и найти положение силы, при котором этот угол будет максимальным.

1. Построим эпюру изгибающих моментов М₁ от силы F₁.Для этого найдем опорную реакцию А₁. Из уравнения равновесия для системы в целом 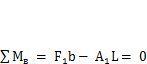найдем 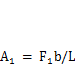.Максимальный изгибающий момент под силой Fj

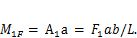
2. В качестве вспомогательного состояния возьмем загружение балки единичным моментом F₂= 1 Н-м в том сечении, поворот которого надо определить (рис. 3.9, б). Строим эпюру изгибающих моментов для этого случая нагружения. Опорные реакции А₂ = -В₂ = 1/L,изгибающие моменты

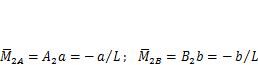
Оба момента отрицательные, так как направлены по часовой стрелке. Эпюры строятся на растянутом волокне.

3. Вычисляем угол поворота по формуле (3.11), выполняя перемножение по двум участкам,

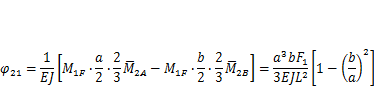
Обозначив 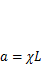, можно получить это выражение в более удобной форме:

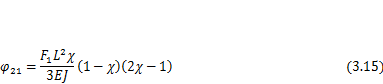
График зависимости угла поворота от положения силы F₁показан на рис. 3.9, в. Продифференцировав это выражение, из условия 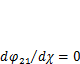найдем положение силы, при котором угол наклона балки под ней будет наи­большим по абсолютному значению. Это произойдет при значениях равных 0,21 и 0,79.