Геометрическая иллюстрация решения задач ЛП

Пусть задана стандартная математическая модель задачи с двумя неизвестными:

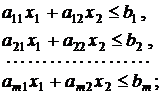(1.7)

(1.8)

Нахождение решения этой модели на основе ее геометрической интерпретации включает следующие этапы.

1. В плоскости х₁0 х₂ строят прямые, уравнения которых получаются в результате замены в ограничениях (1.7) модели знаков неравенств на знаки точных равенств.

2. Находят полуплоскости, определенные каждым неравенством системы.

3. Находят выпуклый многоугольник решений всей системы (1.7).

4. Строят нормальный вектор целевой функции , причем, начало вектора совмещают с началом координат и строят прямую .

5. Передвигают эту прямую в направлении вектора , в результате либо находят вершину или отрезок, в которой целевая функция принимает наибольшее значение, либо устанавливают неограниченность сверху этой функции на множестве допустимых решений.

6. Если функция ограничена, то определяют и вычисляют значение функции в этой точке .

При геометрической интерпретации задач ЛП могут встретиться случаи, изображенные на рис. 2.1. - 2.4.

Рис. 2.1. задача ЛП имеет единственное решение .

Рис. 2.2. задача ЛП имеет бесчисленное множество решений, т.к. целевая функция достигает максимума на отрезке [М; N].

Рис. 2.3. задача ЛП не имеет решения, т.к. функция неограниченна сверху.

Рис. 2.4. задача ЛП не имеет решения, т.к. система (1.7) несовместна.

Рис. 2.1. Рис. 2.2.

Рис. 2.3. Рис. 2.4.

Пример. Для производства двух видов изделий А и В предприятие использует три вида сырья S₁ , S₂ , S₃. Нормы расхода сырья каждого вида на изготовление единицы продукции данного вида приведены в таблице 2.1.

Прибыль от реализации одного изделия каждого вида равна с₁и с₂ , а общее количество сырья вида равно , . Считая, что изделия А и В могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий будет максимальной.

Сырье	А	В	Запасы
S1	а11 = 12	а12 = 4	в1 = 300
S2	а21 = 4	а22 = 4	в2 = 120
S3	а31 = 3	а32 = 12	в3 = 252
Прибыль	с1 = 30	с2 = 40

Решение. Обозначим через х₁ и х₂количествоизделий первого и второго вида в плане предприятия. Поскольку производство продукции ограничено только сырьем каждого типа S_i, то получим условия:

12х₁ + 4х₂ £ 300,

4х₁ + 4х₂ £ 120, (1)

3х₁ +12х₂ £ 252,

Переменные х₁ и х₂ не могут быть отрицательными по смыслу задачи.

Вычислим прибыль от реализации продукции и получим:

Итак, мы получили стандартную модель с двумя переменными.

Решим задачу линейного программирования геометрически, придерживаясь плана, приведенного ранее.

1. Строим прямые l₁, l₂, l₃:

l₁ : 12х₁ + 4х₂ = 300, по двум точкам А₁ (25, 0) и В₁ (0; 75);

l₂ : 4х₁ + 4х₂ = 120, по двум точкам А₂ (30; 0)и В₂ (0, 30);

l₃ : 3х₁ + 12х₂ = 252, по двум точкам А₃ (84, 0 )и В₃ (0, 21).

Обратимся к неравенствам (1). Отметим те полуплоскости, которые им удовлетворяют. Учтем на чертеже и неотрицательность переменных х₁ и х₂,и получим многоугольник ОВ₃ЕСА₁ решений данной системы неравенств (см. рис. 2.5).

2. Построим нормальный вектор и прямую (l): 30х₁+40х₂ = 0.

3. Передвигая прямую в направлении вектора , получим, что в точке Е (12, 18) целевая функция будет иметь наибольшее значение. Координаты этой точки находим как координаты точки пересечения прямых и , решая систему уравнений:

4. Запишем окончательный ответ:

Рис. 2.5.

Наибольшая прибыль будет равна 1080 (у.е).