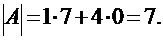Определители квадратных матриц

Необходимость введения понятия определителя – некоторого числа, характеризующего любую квадратную матрицу A, тесно связана с задачей решения систем линейных уравнений (см. тему 2.2), а также с некоторыми другими при­ложениями матричной алгебры.

Для обозначения определителя матрицы A наиболее часто используются следующие символы: |А|, Δ_А, detA.

Определение.Определителем первого порядка, или определителем квадратной матрицы первого порядка 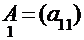называется ее единственный элемент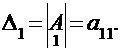

Определение.Определителем второго порядка, или определителем квадратной матрицы второго порядка, называется число, которое вычисляется по правилу: разность произведений элементов главной и побочной диагоналей:

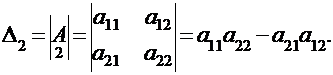
Определение.Определителем третьего порядка, или определите­лем квадратной матрицы третьего порядка, называется число, равное:

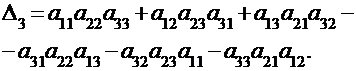
Замечание.Эта формула может быть получена, например, по правилу Саррюсса, состоящему в следующем: приписать к определителю третьего порядка справа два первых его столбца, не меняя их порядка, и составить сумму произведений элементов главной диагонали и параллельных ей диагоналей, из которых затем вычесть сумму произведений элементов побочной и двух параллельных ей диагоналей. Таким образом, вычисления надо проводить по схеме:

Определители более высоких порядков (т.е. при n > 3) вычисляются дру­гими способами, основанными на ряде новых понятий таких, как минор элемента матрицыи алгебраическое дополнение элемента матрицы.

Определение. Минором М_ij элемента a_ij квадратной матрицы A n-го порядка называется определитель матрицы на единицу меньшего порядка, полученной из матрицы A вычеркиванием i-ой строки и j-го столбца.

Например, минором элемента 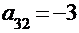квадратной матрицы: 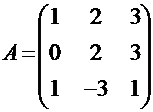будет число, равное: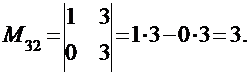

Определение. Алгебраическим дополнением A_ij элемента a_ij квад­ратной матрицы A порядка n называется его минор, взятый со знаком 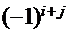, т.е.:

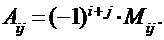Например, алгебраическое дополнение того же элемента, что и в пре­дыдущем примере, будет равно: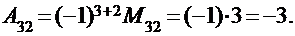

Для установления алгоритма вычисления определите­лей любого порядка сформулируем следующую теорему.

Теорема Лапласа.Определитель квадратной матрицы равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения.

Практическое значение теоремы Лапласа состоит в том, что она позволяет свести вычисление определителя n-го порядка к вычислению n более “простых” определителей (n – 1)-го порядка. Пос­ледовательно применяя такое разложение, в конце концов приходят к конечной сумме, состоящей из чисел, умноженных на определители второго порядка, вычисление которых не вызывает трудностей.

ПРИМЕР: Вычислить определитель матрицы

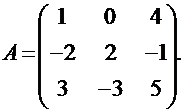
Согласно теореме Лапласа, для первой строки матрицы можно записать:

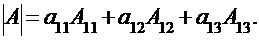
Поскольку элемент 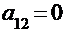, найдем алгебраические дополнения:

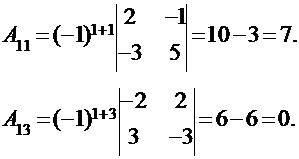
Таким образом,