Свойство 1. (Определитель транспонированной матрицы)

При транспонированииопределитель матрицыне меняется.

Другими словами, определитель транспонированной матрицы равен определителю исходной матрицы.

Это означает, что строки и столбцы определителя равноправны.

▲ Заменив вопределителе (2.8) каждую строку столбцом с тем же номером, получим новый определитель

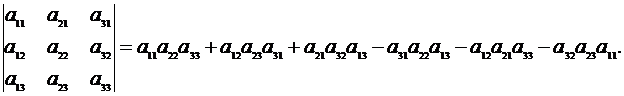
Сравнивая это равенство с равенством (2.8), заключаем, что определители равны, т.к. равны правые части указанных равенств. ▼

Свойство 2. (Антисимметричность (перестановка двух строк))

При перестановке двух строк (столбцов) определительменяет знак.

▲ В определителе (2.8) переставим, например, второй и третий столбцы.

Тогда

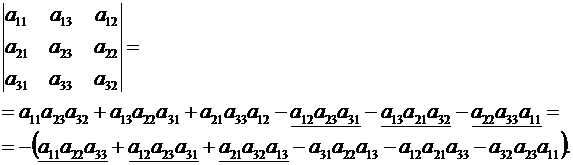
Алгебраическая сумма в скобке равна правой части формулы (2.8),

новый определитель отличается от исходного определителя

только знаком.

Другие случаи рассматриваются аналогично. ▼

Свойство 3

Определитель с двумя одинаковыми строками (столбцами) равен нулю.

▲ Определитель (2.8) обозначим через символ .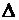

Пусть он содержит два одинаковых столбца.

.

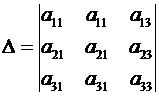Переставивэти столбцы, получим тот же определитель .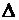

С другой стороны, по свойству 2 определитель изменит знак, т.е.

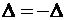, откуда . ▼

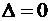Свойство 4

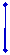Если все элементы некоторой строки (столбца) определителя состоят из нулей, то определитель равен нулю.

▲ В самом деле, в каждое произведение алгебраической суммы в правой части (2.8) входит один элемент строки (столбца), состоящей из нулей.

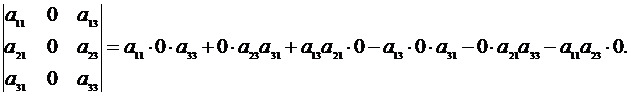
Поэтому все слагаемые, из которых состоит определитель, будут равны нулю. ▼

Свойство 5. (Вынесение общего множителя)

Множитель, общий для элементов некоторой строки (столбца), можно выносить за знак определителя.

▲ Пусть в определителе (2.8) элементы второго столбца имеют общий множитель .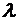

Тогда

,

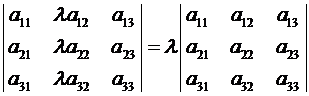т.к.

.

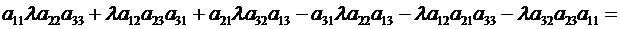
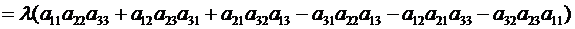Аналогично рассматриваются случаи, когда общий множитель имеют элементы 1-го или 3-го столбца, а также элементы любой строки. ▼

Следствие. Если 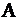квадратная матрица порядка 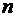и 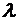– вещественное число, то определитель матрицы 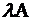есть ;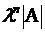

иначе говоря,

.

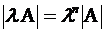▲ В этом случае 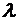является сомножителем каждой из 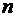строк (столбцов) матрицы .

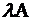Если вынести 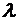из каждой строки (столбца) определителя, то остается . ▼

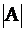Свойство 6

Определитель, содержащий две пропорциональные строки (столбца) равен нулю.

▲ Действительно, выделяя общий множительэлементов (коэффициент пропорциональности) одной из этих строк (столбцов) и вынося его за знакопределителя, получаем определительс двумя одинаковыми столбцами, равныйнулю. ▼

Свойство 7

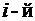Если все элементы строки ( 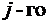столбца) определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей,у которых все строки (столбцы),

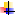кроме 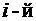строки ( 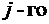столбца), те же, что и у данного определителя,

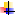
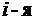строка ( 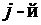столбец) одного определителя состоит из первых слагаемых элементов 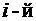строки ( 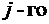столбца) данного определителя,

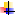а 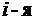строка ( 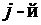столбец) другого определителя – из вторых слагаемых элементов 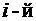строки ( 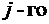столбца).

Доказать самостоятельно.

Свойство 8. (Прибавление кратной строки)

Определитель не изменится, если к элементам одной из его строк (столбцов) прибавить соответствующие элементы другой строки (столбца), умноженные на один и тот же множитель.

▲ Пусть, например, к элементам 3-го столбцаопределителя (2.8) прибавлены соответствующие элементы 2-го столбца, умноженные на множитель .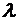

Тогда

,

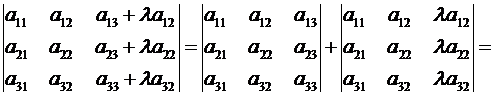
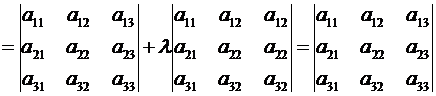поскольку

. ▼

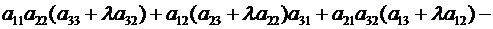
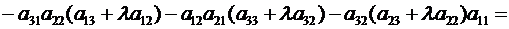
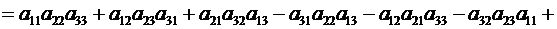
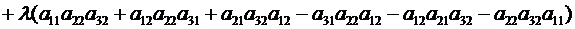Замечание.

(Добавление строки к строке,умноженной на число.)

Как было показано, добавление строки, умноженной на число, к другой строке не влияет на величину определителя.

Заметим, однако, что добавление строки к другой строке, умноженной на число, не является тем же самым и приводит к иным результатам.

Например, добавляяк первой строке, умноженной на число 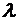, вторую строку, получим определитель

.

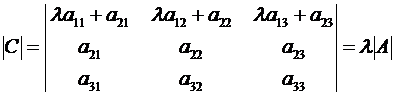Это происходит в связи с тем, что 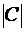получают 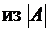путем умноженияпервой строки 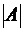на 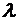и добавления к нейвторой строки.

Первый из этих двух шагов, как было показано, изменяет 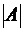на 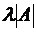, а второй не изменяет этой величины.

Отсюда .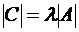

Таким образом, в то время как строка, умноженная на число и добавленная к строке, не оказывает влияния наопределитель,

добавление строки к строке, умноженной на число, имеетсвоим последствием то, что определитель оказывается умноженным на этот множитель.

Эти же действия справедливы для столбца.

Применяя вышеуказанные свойстваопределителей, можно упростить задачу вычисленияопределителей.

Преобразования, не изменяющие величинуопределителя, называются элементарными.