Контрольных работ по высшей математике
(для студентов факультета заочного обучения направления подготовки 120700 «Землеустройство и кадастры»)
Пермь – 2012
Составители: С. Б. Югова, Н. В. Деменева.
Методические указания к выполнению контрольных работ по высшей математике (для студентов факультета заочного обучения направления подготовки 120700 «Землеустройство и кадастры») / С. Б. Югова, Н. В. Деменева; Пермь, Пермская ГСХА, 2012. – 82 с.
Рецензент: Н. К. Шестакова, кандидат физ.-мат. наук, доцент, доцент кафедры физики «Пермской ГСХА».
Методические указания составлены в соответствии с рабочей программой по дисциплине «Высшая математика» факультета заочного обучения направления подготовки 120700 «Землеустройство и кадастры». Методические указания включают три контрольные работы по основным разделам высшей математики: элементы линейной алгебры и аналитической геометрии, математический анализ, основы теории вероятностей и математической статистики. Методические указания предназначены для использования как на занятиях, так и при самостоятельной работе студентов факультета заочного обучения направления «Землеустройство и кадастры» ПГСХА.
2-е издание, переработанное и дополненное
Печатается по решению методической комиссии
факультета землеустройства и кадастра
(протокол № 4 от 14 февраля 2012 г. ).
СОДЕРЖАНИЕ
РАЗДЕЛ 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ.. 4
ТЕМА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.. 4
ТЕМА 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ.. 10
ТЕМА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ. 16
РАЗДЕЛ 2. МАТЕМАТИЧЕСКИЙ АНАЛИЗ. 23
ТЕМА 4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.. 23
ТЕМА 5. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 36
ТЕМА 6. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.. 43
ТЕМА 7. КОМПЛЕКСНЫЕ ЧИСЛА.. 54
ТЕМА 8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.. 55
ТЕМА 9. ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ.. 61
РАЗДЕЛ 3. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.. 67
ТЕМА 10. СЛУЧАЙНЫЕ СОБЫТИЯ, СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.. 67
ЛИТЕРАТУРА.. 82
РАЗДЕЛ 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И
АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
ТЕМА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Задание 1.Решить систему линейных алгебраических уравнений по правилу Крамера, методом обратной матрицы и методом Гаусса.
1. 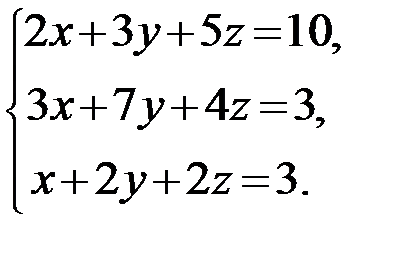 2.
2. 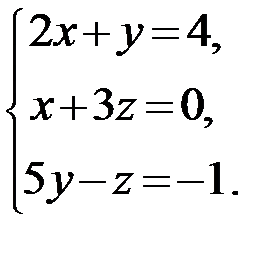
3. 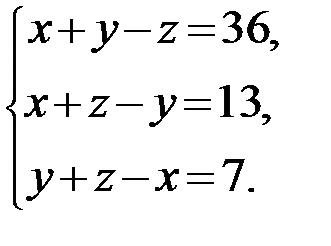 4.
4. 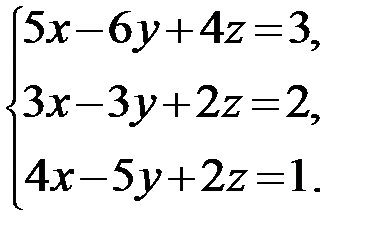
5. 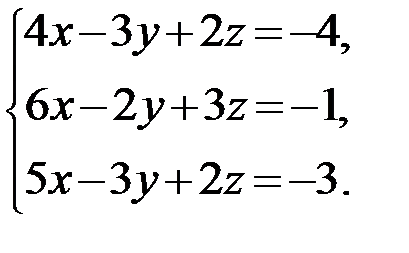 6.
6. 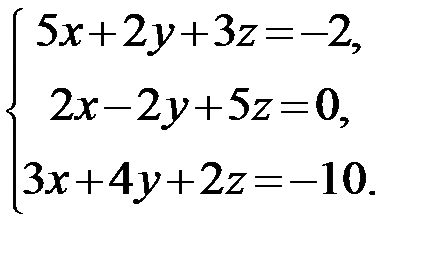
7. 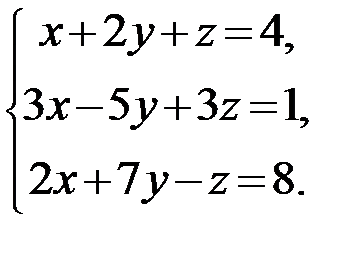 8.
8. 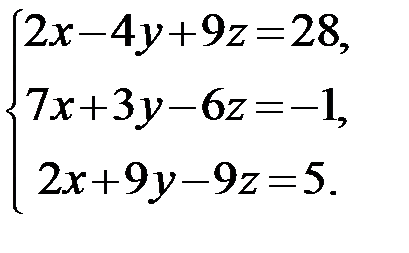
9. 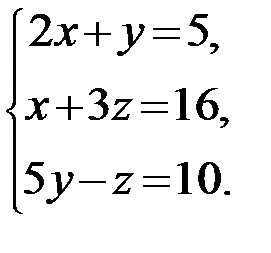 10.
10. 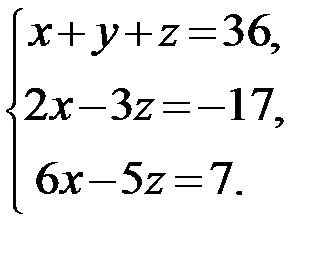
11. 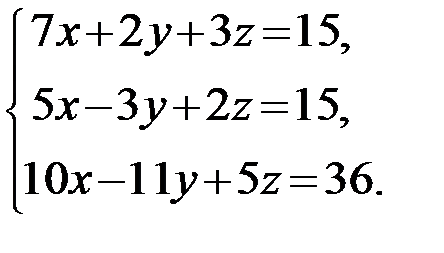 12.
12. 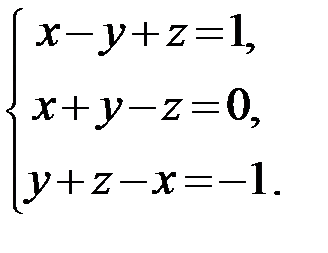
13. 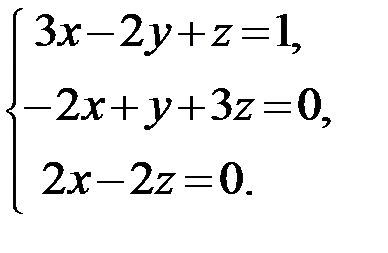 14.
14. 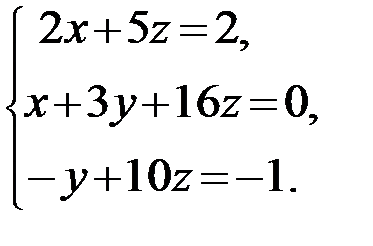
15. 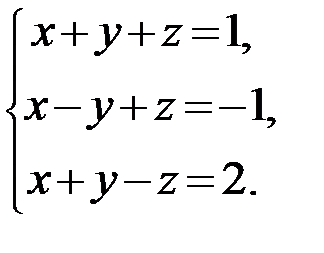 16.
16. 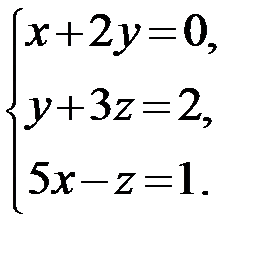
17. 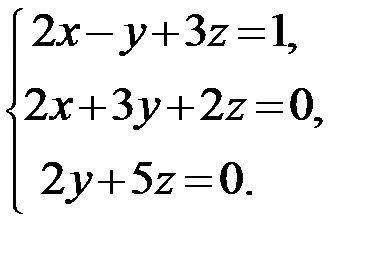 18.
18. 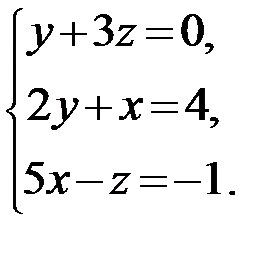
19. 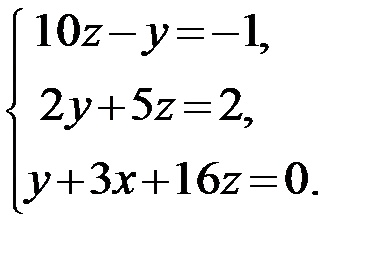 20.
20. 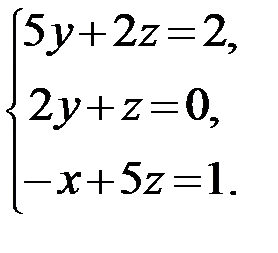
21. 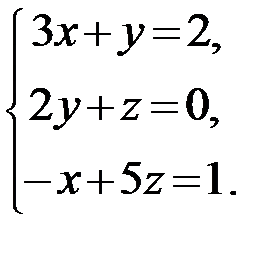 22.
22. 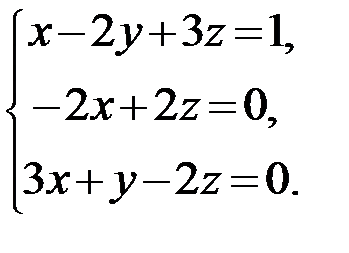
23. 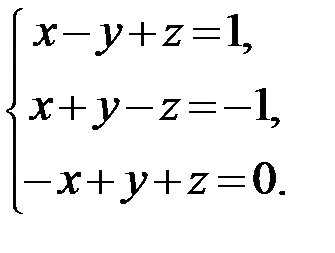 24.
24. 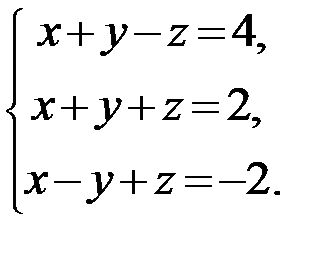
25. 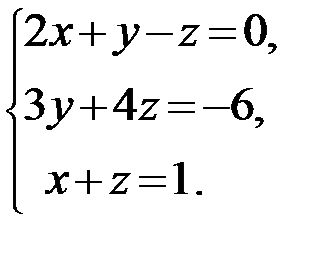 26.
26. 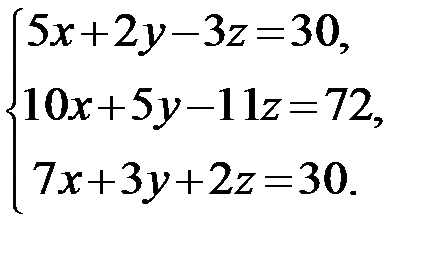
27. 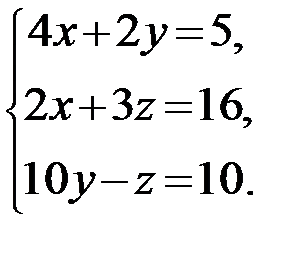 28.
28. 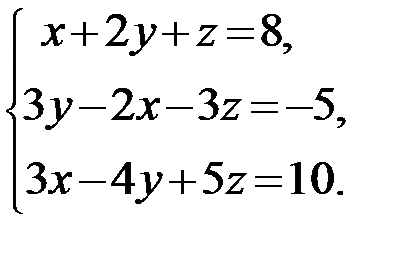
29. 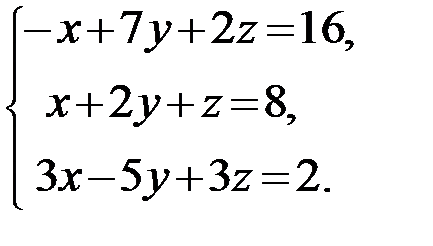 30.
30. 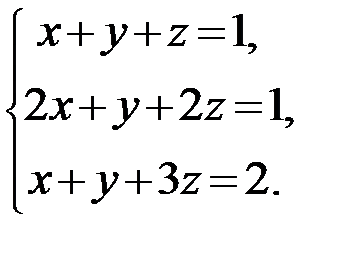
31. 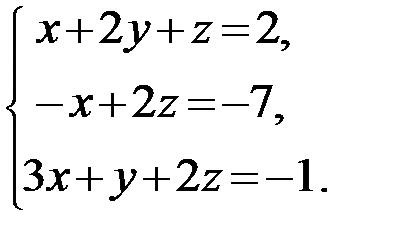 32.
32. 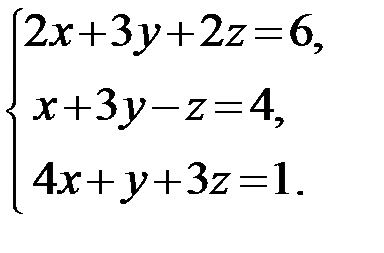
Пример.
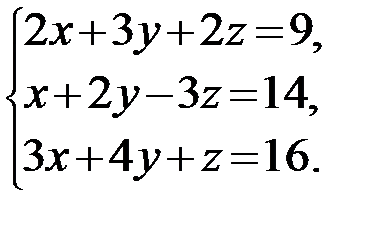
Решение.
1. Правило Крамера.
Запишем определитель системы  – определитель, составленный из коэффициентов при неизвестных, и вычислим его по правилу треугольника:
– определитель, составленный из коэффициентов при неизвестных, и вычислим его по правилу треугольника:
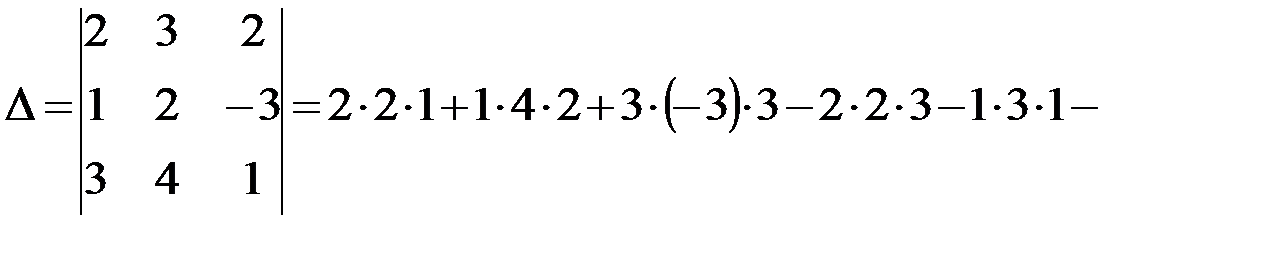
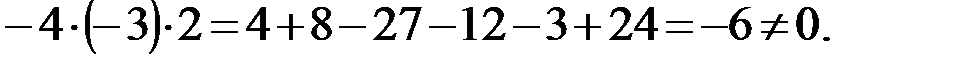
Система является определённой.
Далее вычисляем определители 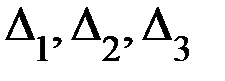 . Определитель
. Определитель 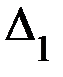 получается из
получается из  заменой первого столбца числами, расположенными в правой части уравнений:
заменой первого столбца числами, расположенными в правой части уравнений:
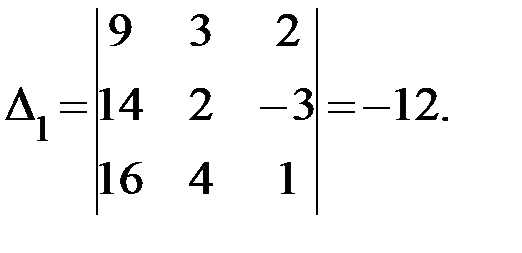
Определитель 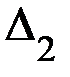 получается из
получается из  заменой второго столбца числами, расположенными в правой части уравнений:
заменой второго столбца числами, расположенными в правой части уравнений:
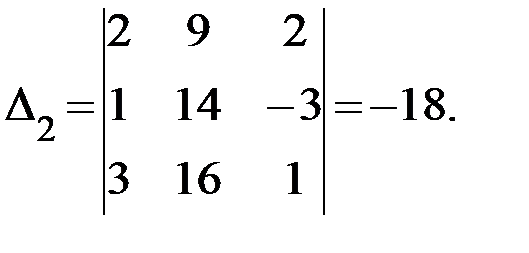
И определитель 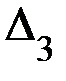 получается из
получается из  заменой третьего столбца числами, расположенными в правой части уравнений:
заменой третьего столбца числами, расположенными в правой части уравнений:
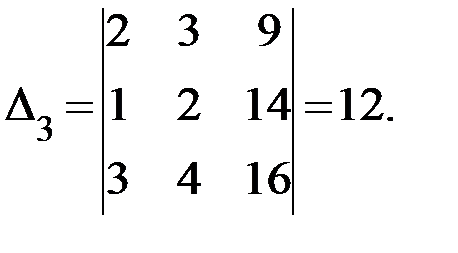
По формулам Крамера находим неизвестные системы:
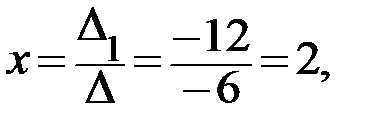
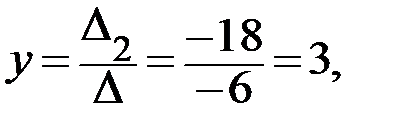
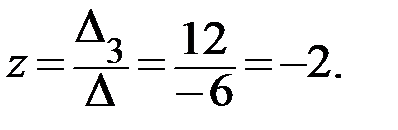
Ответ: 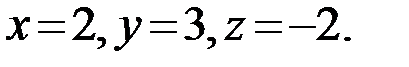
2. Метод обратной матрицы.
Запишем матрицу системы – матрицу, составленную из коэффициентов при неизвестных:
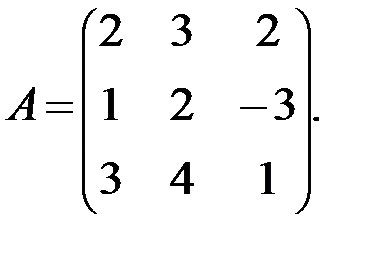
Далее запишем матрицу свободных элементов – матрицу-столбец, составленную из чисел, расположенных в правой части уравнений:
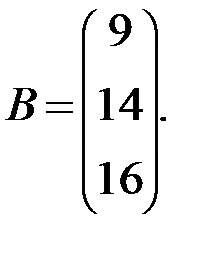
И запишем матрицу неизвестных:
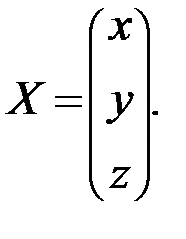
Тогда систему можно переписать в виде матричного уравнения: 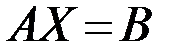 , решение которого находим по формуле
, решение которого находим по формуле 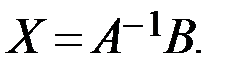
Прежде всего найдём матрицу 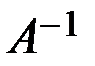 , обратную матрице
, обратную матрице 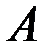 , по формуле:
, по формуле:
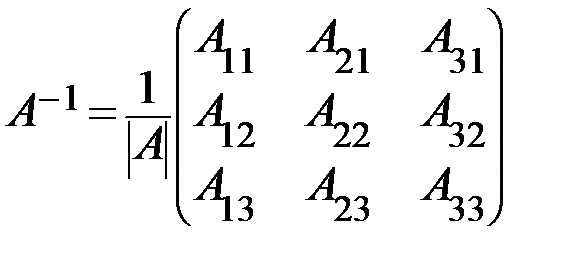 .
.
Определитель системы 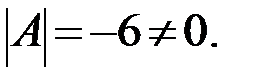 Следовательно для матрицы
Следовательно для матрицы 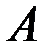 существует обратная. Вычислим алгебраические дополнения элементов матрицы
существует обратная. Вычислим алгебраические дополнения элементов матрицы 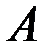 по формуле
по формуле 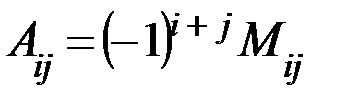 :
:
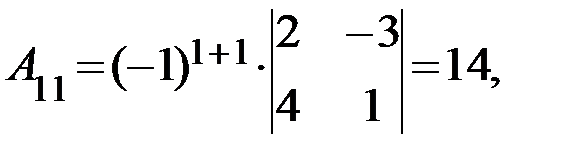
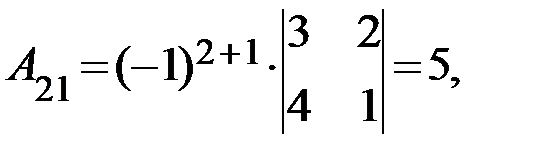
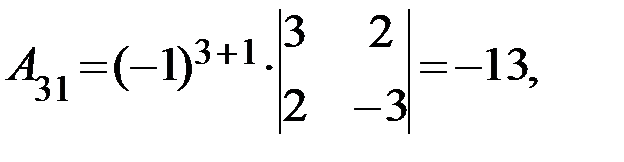
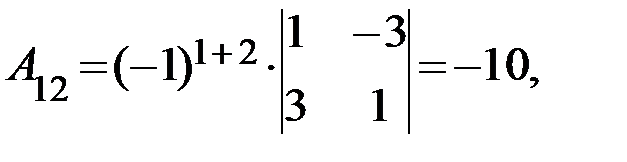
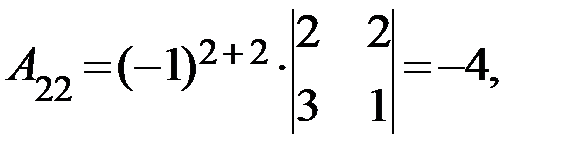
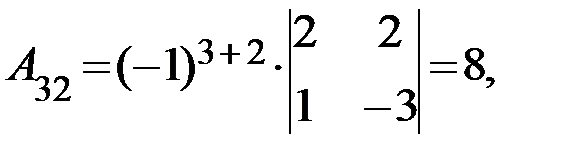
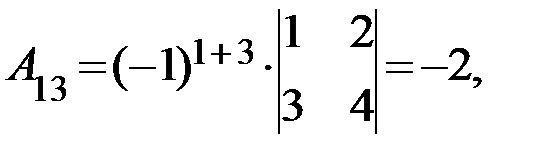
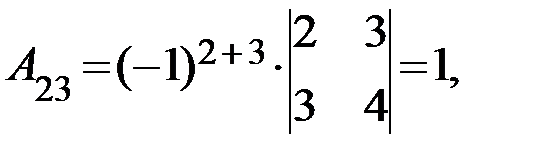
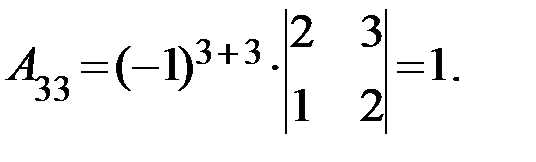
Отсюда 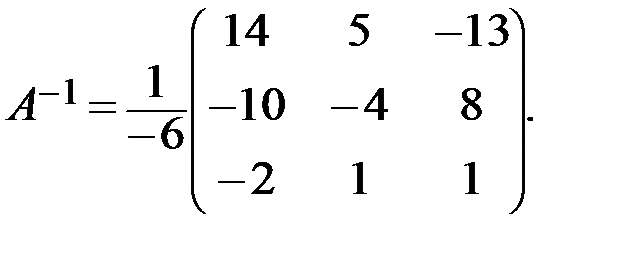
Тогда:
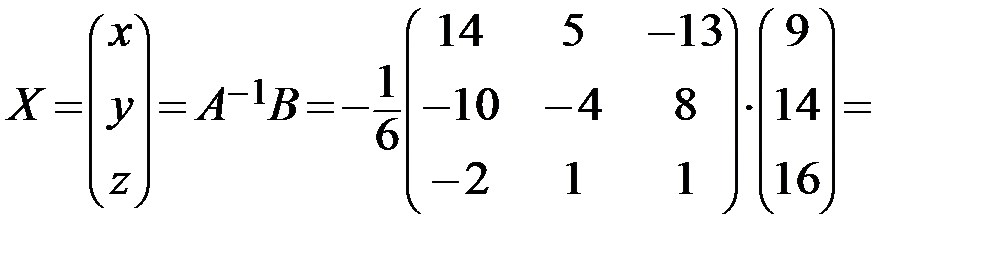
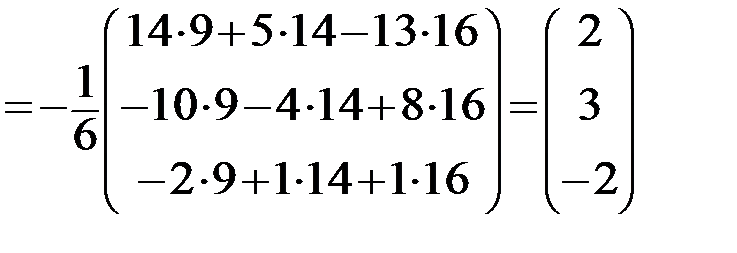 .
.
Итак, 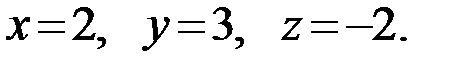
Ответ: 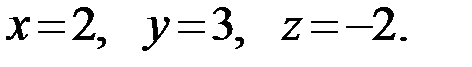
3. Метод Гаусса.
Составим расширенную матрицу и выполним над ней элементарные преобразования:
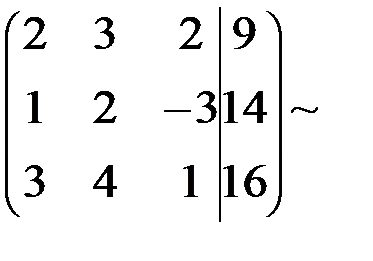
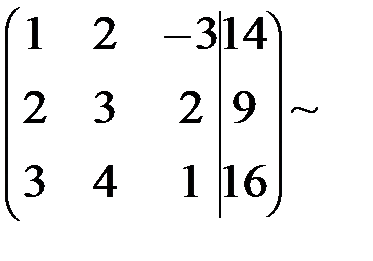
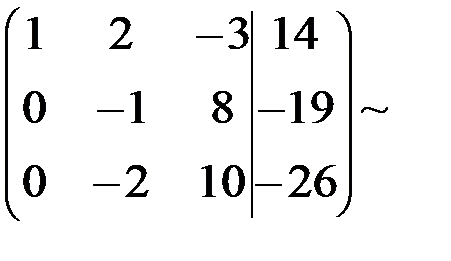
~ 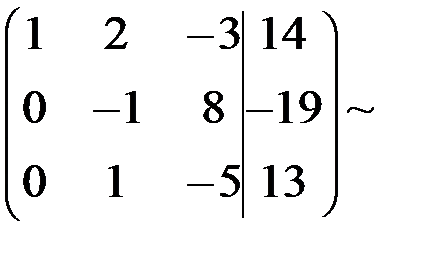
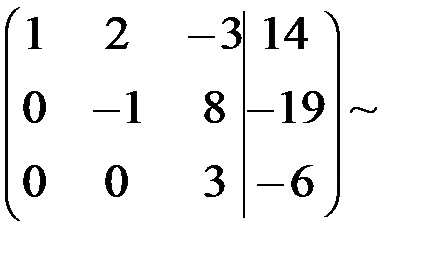
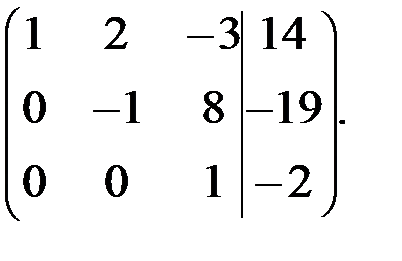
Здесь выполнены следующие преобразования:
а) первую и вторую строчки поменяли местами;
б) ко второй строке прибавили первую, умноженную на (–2), к третьей строке прибавили первую, умноженную на (–3);
в) третью строчку разделили на (–2);
г) к третьей строке прибавили вторую;
д) третью строчку разделили на 3.
Последней матрице соответствует следующая система уравнений:
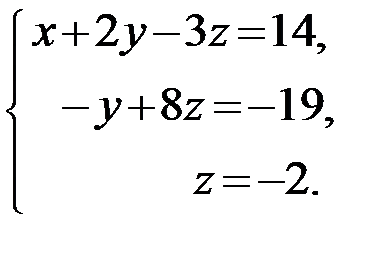
Из этой системы последовательно находим:
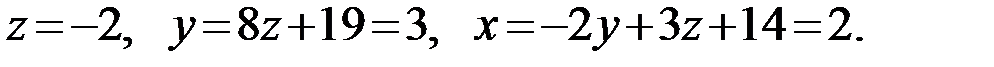
Ответ: