Символический метод анализа электрической цепи
КАФЕДРА АРЭО
КУРСОВАЯ РАБОТА
«Теоретические основы электротехники»
Вариант №75
Выполнил: студент 2 курса
Бондарай А. А.
Шифр: РС-141775
Специальность:25.05.03
Проверил: доцент Сосновский М.Ю.
ИРКУТСК 2016 г.
Содержание Стр.
1. Символический метод анализа электрической цепи…………...4
1.1. Расчёт действующих и мгновенных значений токов и напряжений………………………………….……………...4
1.2. Построение топографической диаграммы цепи…………7
1.3. Определение комплексной частотной передаточной функции…………………………………………………….8
2. Определение переходной функции цепи h(t)………………….12
2.1. Классический метод определения……………………….12
2.1.1.Расчет установившейся составляющей………………13
2.1.2.Определение общего вида свободной составляющей………………………………………….13
2.1.3.Определение начальных условий…………………….14
2.1.4.Вычисление постоянных интегрирования………...…15
2.2. Операторный метод определения………………….……16
3. Реакция цепи на воздействия прямоугольного импульса…….19
Используемая литература………………………………………20
Цель курсовой работы
Курсовая работа (КР) по дисциплине «Теоретические основы электротехники» имеет целью закрепление знаний студентов по составляющим разделам учебной дисциплины. В ходе самостоятельного выполнения КР студенты приобретают практические навыки анализа и расчета электрических цепей переменного синусоидального тока в установившихся режимах, построения частотных характеристик, а также анализа цепей при переходных режимах [1].
Исходные данные
Вариант численных данных №1
L=1мГн
C=7мкФ
R1=4Ом
R2 =180Ом
R3 =3Ом
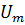=36В
f=1600Гц
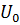=12 В
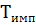=3τ
Схема электрической цепи изображена на рис.1.
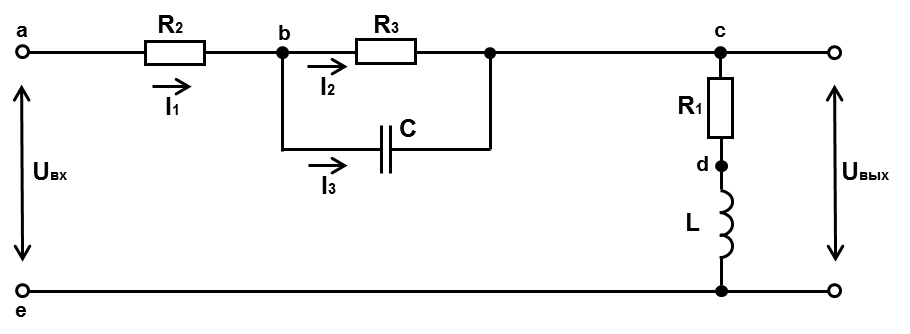
Рис.1. Схема электрической цепи
Символический метод анализа электрической цепи
(метод комплексных амплитуд)
Рассчитаем мгновенные и действующие значения токов во всех ветвях, а также выходного напряжения
Приложенное входное напряжения:
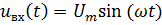
Комплексная амплитуда напряжения:
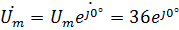
Рассчитаем индуктивное сопротивление катушки и емкостное сопротивление конденсатора для заданной частоты:
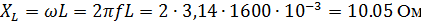
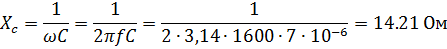
Комплексные сопротивления элементов цепи:
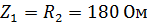
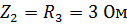
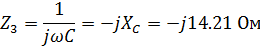
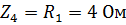
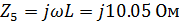
Расчет комплексных амплитуд токов ведется аналогично расчета цепей постоянного тока по схеме, изображенной на рис. 2.
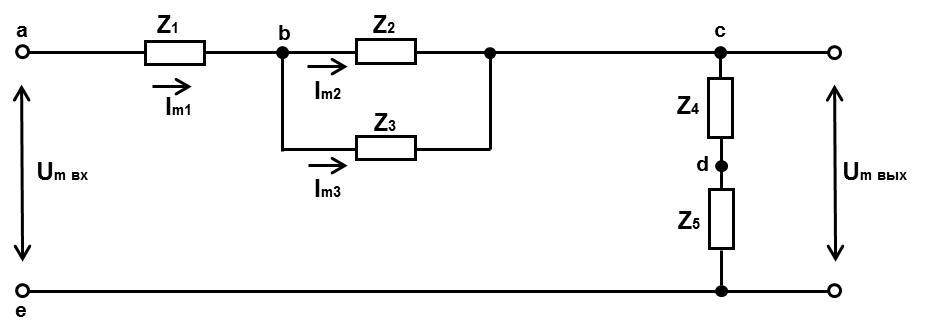
Рис.2.Схема комплексного представления элементов
Находим входное сопротивление всей цепи по отношению к точкам, где приложено входное напряжение:
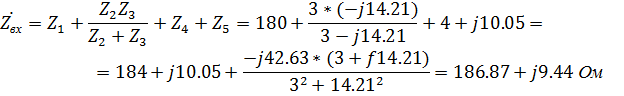
По закону Ома находим комплексную амплитуду тока в первой ветви:
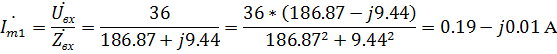
Или в показательной форме:
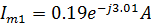
Найдем токи второй и третьей ветвей по формуле «разброса токов» [2]:
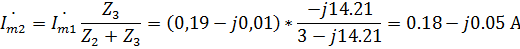
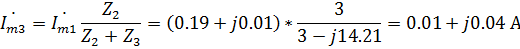
В показательной форме:
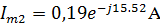
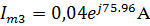
Мгновенные значения токов:
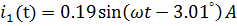
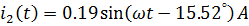
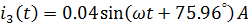
Действующие значения токов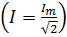 
:
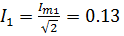A
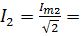0.13A
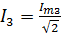= 0.03A
Комплексную амплитуду выходного напряжения найдем по закону Ома:
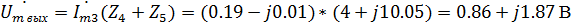
В показательной форме:
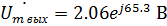
Мгновенное значение:
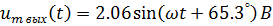
Действующее значение:
U=1.46B
Классический метод
Классический метод предполагает представление искомой величины (в данном случае выходного напряжения) в виде суммы установившейся и свободной составляющей [2]:
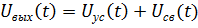
Так как необходимое напряжение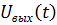 
нужно рассчитать на 2-ух элементах (сопротивления 
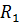и индуктивности 
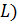, то для расчета нужно взять ток на индуктивности и умножить на сопротивление :
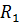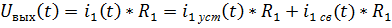
Операторный метод
Действия операторным методом при нулевых начальных условиях в значительной мере подобны действиям при анализе символическим методом цепей синусоидального тока при замене в выражениях сопротивлений комбинации «jω» на букву «p» [2]. Поэтому можем воспользоваться полученным выражением для комплексной частотной характеристики, записав на месте «jω» букву «p». Таким образом, мы найдем то, что называется передаточной функцией:
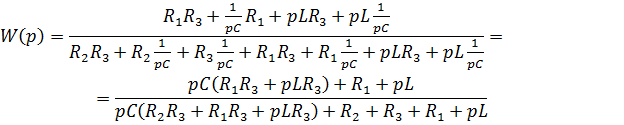
С помощью этой функции легко можно записать операторное выходное напряжение при заданном операторном входном напряжении:
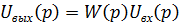
В нашем случае на входе действует постоянная ЭДС, равная 1В. Ее операторным изображением является 1/p. Значит операторным изображением переходной функции h(t) будет:
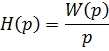
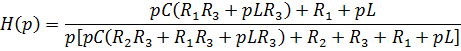
Остается найти оригинал по формуле разложения:
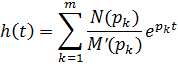
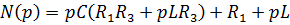
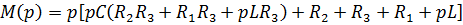
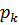-корни многочлена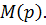 
; 
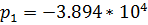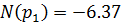
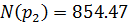
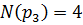
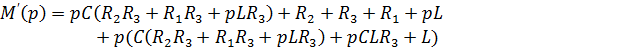
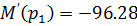
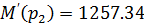
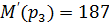
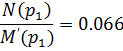
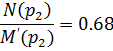
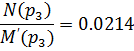
Подставляем в формулу разложения:
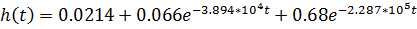
В последнем уравнении константы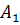 
и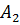 
не сходятся с раннее рассчитанными константами, найденные классическим методом расчета, это свидетельствует о том, что допущена ошибка в составлении уравнений для расчета свободной составляющей тока, либо имеется ошибка в математических расчетах операторного метода.
График переходной функции изображен на рис.8.
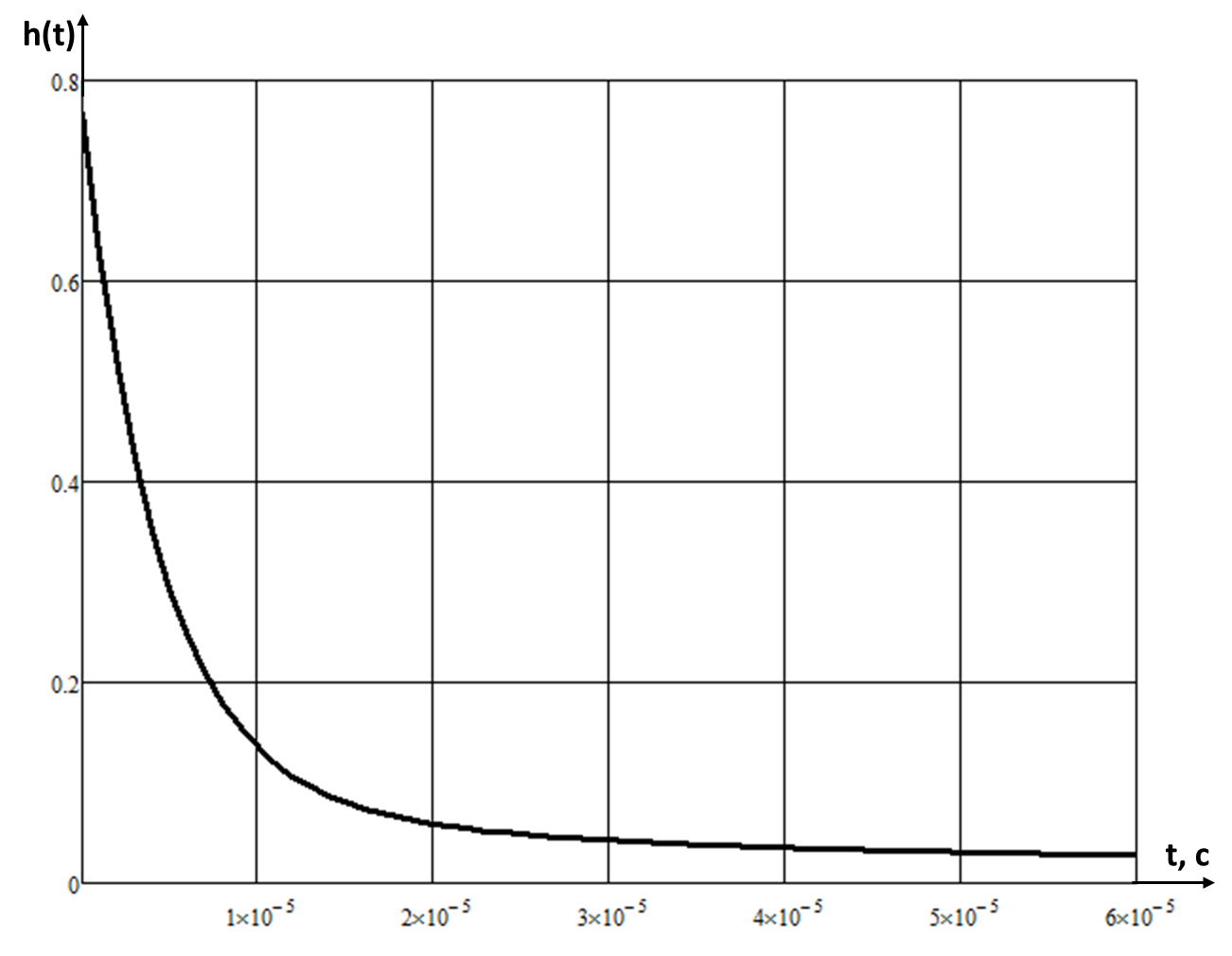
Рис.8. График переходной функции
КАФЕДРА АРЭО
КУРСОВАЯ РАБОТА
«Теоретические основы электротехники»
Вариант №75
Выполнил: студент 2 курса
Бондарай А. А.
Шифр: РС-141775
Специальность:25.05.03
Проверил: доцент Сосновский М.Ю.
ИРКУТСК 2016 г.
Содержание Стр.
1. Символический метод анализа электрической цепи…………...4
1.1. Расчёт действующих и мгновенных значений токов и напряжений………………………………….……………...4
1.2. Построение топографической диаграммы цепи…………7
1.3. Определение комплексной частотной передаточной функции…………………………………………………….8
2. Определение переходной функции цепи h(t)………………….12
2.1. Классический метод определения……………………….12
2.1.1.Расчет установившейся составляющей………………13
2.1.2.Определение общего вида свободной составляющей………………………………………….13
2.1.3.Определение начальных условий…………………….14
2.1.4.Вычисление постоянных интегрирования………...…15
2.2. Операторный метод определения………………….……16
3. Реакция цепи на воздействия прямоугольного импульса…….19
Используемая литература………………………………………20
Цель курсовой работы
Курсовая работа (КР) по дисциплине «Теоретические основы электротехники» имеет целью закрепление знаний студентов по составляющим разделам учебной дисциплины. В ходе самостоятельного выполнения КР студенты приобретают практические навыки анализа и расчета электрических цепей переменного синусоидального тока в установившихся режимах, построения частотных характеристик, а также анализа цепей при переходных режимах [1].
Исходные данные
Вариант численных данных №1
L=1мГн
C=7мкФ
R1=4Ом
R2 =180Ом
R3 =3Ом
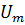=36В
f=1600Гц
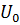=12 В
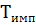=3τ
Схема электрической цепи изображена на рис.1.
Рис.1. Схема электрической цепи
Символический метод анализа электрической цепи
(метод комплексных амплитуд)