А – функциональная схема; б – УГО

Полный двоичный четырехразрядный сумматор изображается на схемах с использованием УГО, показанного на рисунке 14.8. Обратите внимание, что в этом обозначении входы двоичного слова 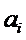объединены в отдельное поле. Точно так же объединены входы двоичного слова 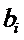. Вход и выход сигналов переноса в приведенном УГО микросхемы тоже выделены в отдельные поля. Это не обязательно, и не требуется ГОСТом, однако изображенная таким образом микросхема намного более наглядно отображает свои функции.

Приведенная на рисунке 14.8 схема не оптимизирована по быстродействию, она служит лишь для пояснения принципа действия многоразрядного двоичного сумматора. В применяемых на практике схемах никогда не допускают последовательного распространения переноса через все разряды многоразрядного сумматора, т. к. это снижает его быстродействие.

Для увеличения скорости работы двоичного сумматора используется отдельная схема формирования переносов для каждого двоичного разряда. Таблицу истинности для такой схемы легко получить из алгоритма суммирования двоичных чисел, а затем применить хорошо известные нам принципы построения цифрового устройства по произвольной таблице истинности.

3.2 Способы ускорения переноса в сумматорах

При неблагоприятных сочетаниях цифра переноса в параллельном сумматоре может распространяться через все разряды. Поэтому наибольшее время сложения двух 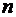разрядных чисел в параллельном сумматоре определяется как

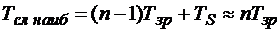, (14.8)

где 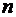– число разрядов в регистрах;

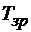– время задержки цифры переноса ;

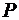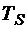– время образования суммы в сумматоре.

Следовательно, быстродействие сумматоров в основном зависит от времени переноса цифры в старшие разряды (см. выражение 14.8).

Поэтому повышение быстродействия сумматоров в основном может быть обеспечено за счет его уменьшения.

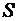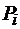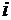Для повышения скорости работы параллельных сумматоров применяют различные приемы, сокращающие время прохождения сигнала переноса через группу одноразрядных сумматоров. Значение суммы и переноса в -м разряде, можно записать в виде

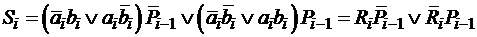. (14.9)

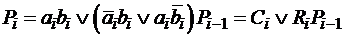, (14.10)

где 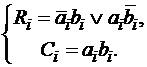(14.12)

Из выражения (14.10) следует, что появление единицы переноса в 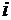-м разряде вызывается двумя причинами:

во-первых, перенос может возникнуть внутри одноразрядного сумматора при ;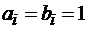

во-вторых, перенос может быть выработан в связи с возникновением единицы переноса в предыдущем разряде (сквозной перенос).

Переносы первого типа образуются во всех разрядах одновременно с поступлением на входы сумматора слагаемых. Переносы второго типа формируются последовательно от младших разрядов к старшим. Основная задача заключается в уменьшении времени распространения сигнала сквозного переноса.

Эта задача решается путем создания схем, где в формировании переноса 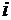-го разряда участвует перенос из ( 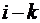)-го разряда. Для этого в старшем ( 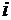-м) разряде необходимо анализировать не только цифры 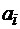и 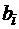, но и цифры младших разрядов 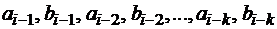. Схемы, построенные для обработки этих цифр, должны срабатывать до поступления единицы переноса из младших разрядов и тем самым ускорять распространение сквозного переноса. То есть, используя (14.10), можно записать, что

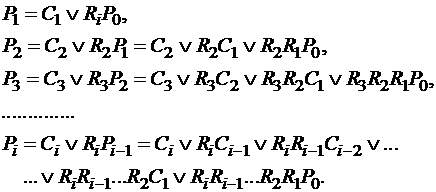(14.13)

Сумматоры, схема которых реализует (14.13) называют сумматорами с параллельным переносом.

3.3. Примеры включения счетчиков и сумматоров в цифровые схемы

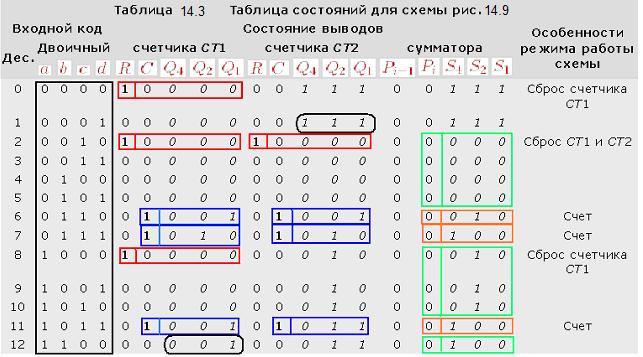
Рассмотрим пример включения счётчиков и сумматоров в схемы. Необходимо заполнить таблицу состояний схемы (рисунок 14.9), включающей счетчики и сумматор, в соответствии с заданной последовательностью входных сигналов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.

Анализ данной схемы показывает, что:

- счетчик СТ 1 сбрасывается (т. е. переходит в нулевое состояние, когда 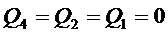) при наличии сигнала сброса 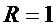. Этот сигнал сброса в данной схеме получается в трех случаях, когда:

* либо на выходе "0" дешифратора генерируется активный сигнал. Это происходит при подаче на его входы кода 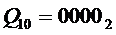, что соответствует входному коду ;

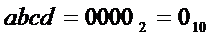* либо на выходе "1" дешифратора генерируется активный сигнал. Это происходит при подаче на его входы кода 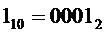, что соответствует входному коду ;

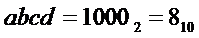* либо на выходе "4" дешифратора генерируется активный сигнал. Это происходит при подаче на его входы кода 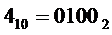, что соответствует входному коду .

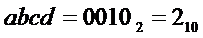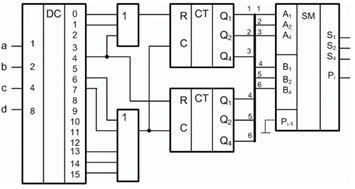
Рисунок 14.9 – Пример схемы с включением счётчиков и сумматора

- счетчик СТ 2 сбрасывается (т. е. переходит в нулевое состояние, когда 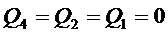) при наличии сигнала сброса 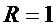. Этот сигнал сброса в данной схеме получается только в одном случае, когда:

* на выходе "4" дешифратора генерируется активный сигнал. Это происходит при подаче на его входы кода 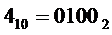, что соответствует входному коду .

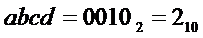- у обоих счетчиков переключение в следующее состояние (счет) происходит одновременно при наличии сигнала счета 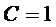. Этот сигнал счета в данной схеме получается в пяти случаях, когда:

* либо на выходе "6" дешифратора генерируется активный сигнал. Это происходит при подаче на его входы кода 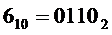, что соответствует входному коду ;

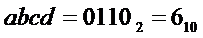* либо на выходе "7" дешифратора генерируется активный сигнал. Это происходит при подаче на его входы кода 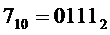, что соответствует входному коду ;

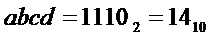* либо на выходе "13" дешифратора генерируется активный сигнал. Это происходит при подаче на его входы кода 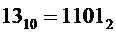, что соответствует входному коду ;

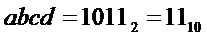* либо на выходе "14" дешифратора генерируется активный сигнал. Это происходит при подаче на его входы кода 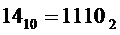, что соответствует входному коду ;

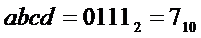* либо на выходе "15" дешифратора генерируется активный сигнал. Это происходит при подаче на его входы кода 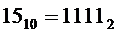, что соответствует входному коду .

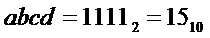Согласно варианту начальное значение на выходах СТ 1 равно 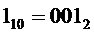, а на выходах СТ 2 оно равно 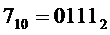. Эти значения поменяются на 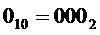при подаче 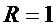или на значение на 1 большее при подаче 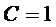. Входной перенос 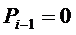, так как этот вход сумматора заземлен в данной схеме. Заполнение таблицы состояний для рассматриваемого примера дано в таблице 14.3.

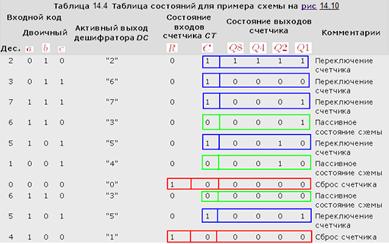
Рассмотрим еще одну схему, включающую в себя дешифратор и счетчик (рисунок 14.10). Необходимо заполнить таблицу состояний схемы в соответствии с заданной последовательностью входных сигналов: 2, 3, 7, 6, 5, 1, 0, 6, 5, 4.

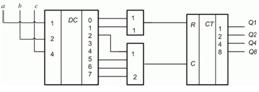
Рисунок 14.10 – Пример схемы с дешифратором и счётчиком

Согласно рисунка входы дешифратора DC включены следующим образом: вход "4" соединен с входным сигналом "с", "2" – со входом "b", "1" – со входом "а". Управляющие входы 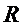и 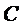счетчика C подключены к выходам логических элементов ИЛИ-1 и ИЛИ-2 соответственно. На входы элемента ИЛИ-1 согласно варианту 1 подаются сигналы с выходов "0" и "1" дешифратора DC. На входы элемента ИЛИ-2 – сигналы с выходов "2", "5", "6" и "7" дешифратора DC.

Перед заполнением таблицы состояний необходимо проанализировать работу схемы. Переключение счетчика СТ будет происходить в том случае, когда на одном из выходов ("2", "5", "6" или "7") дешифратора DC будет логическая1. Рассмотрим подробнее каждый случай.

На выходе "2" будет активный сигнал при наличии на его входах "4", "2" и "1" двоичного кода 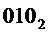, который получается при .

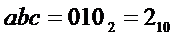На выходе "5" будет активный сигнал при наличии на его входах "4", "2" и "1" двоичного кода 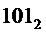, который получается при .

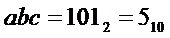На выходе "6" будет активный сигнал при наличии на его входах "4", "2" и "1" двоичного кода 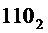, который получается при .

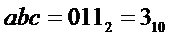На выходе "7" будет активный сигнал при наличии на его входах "4", "2" и "1" двоичного кода 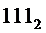, который получается при .

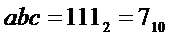Сброс счетчика СТ будет происходить в том случае, когда на одном из выходов ("0" или "1") дешифратора DC будет логическая единица. Рассмотрим подробнее каждый случай.

На выходе "0" будет активный сигнал при наличии на его входах "4", "2" и "1" двоичного кода 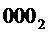, который получается при .

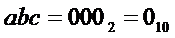На выходе "1" будет активный сигнал при наличии на его входах "4", "2" и "1" двоичного кода 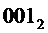, который получается при 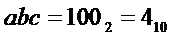. Таблица состояний схемы представлена в таблице 14.4.

Цифровые умножители

Следующим, широко используемым в схемах цифровой обработки сигналов устройством, является цифровой двоичный умножитель. Эти устройства используются как в схемах масштабирования (усилители или аттенюаторы) или гетеродинирования сигналов, так и в составе цифровых фильтров.

Умножение чисел в двоичном виде производится подобно умножению в десятичной системе счисления. При реализации этого алгоритма потребуется перемножить каждый разряд множимого на соответствующий разряд множителя.

Рассмотрим в качестве примера умножение двух четырехразрядных двоичных чисел. Пусть требуется умножить число 1011₂ (11₁₀) на число 1101₂ (13₁₀). В результате умножения мы ожидаем получить число 10001111₂ (143₁₀). Выполним операцию умножения в столбик в двоичной системе, как это показано на рисунке 14.11.

Для формирования произведения требуется вычислить четыречастичных произведения. Обратите внимание,что в двоичной арифметике требуется выполнять умножение только на числа 0 и 1. Это означает, что нужно либо суммировать множимое к сумме остальных частичных произведений, либо нет. В результате для формирования частичного произведения можно воспользоваться логическими элементами "2И", подключенными к каждому двоичному разряду множимого.

Для формирования частичного произведения, кроме операции умножения на один разряд, требуется осуществлять его сдвиг влево на число разрядов, соответствующее весу разряда множителя. Сдвиг можно осуществить простым соединением соответствующих разрядов частичных произведений к необходимым разрядам двоичного сумматора.

Рисунок 14.11 – Выполнение операции умножения

Двоичных чисел в столбик

Для того чтобы принципиальная схема умножителя была похожа на пример двоичного умножения, приведенный на рисунке 14.11, используем УГО микросхем, где входы расположены сверху, а выходы снизу. Это разрешено ГОСТом. В полном соответствии с алгоритмом умножения в столбик нам потребуются три четырехразрядных сумматора.

Принципиальная схема умножителя, реализующая алгоритм двоичного умножения в столбик, приведена на рисунке 14.12.

Формирование частичных произведений в этой схеме осуществляют цифровые микросхемы D1, D3. D5 и D7. В этих микросхемах в одном корпусе содержится сразу четыре логических элемента "2И".

Сумматор, выполненный на микросхеме D6, суммирует первое и второе частные произведения. При этом младший разряд первого частного произведения не нуждается в суммировании. Поэтому он подается на выход умножителя непосредственно (разряд М0).

Второе частное произведение должно быть сдвинуто на один разряд. Это осуществляется тем, что младший разряд выходного числа сумматора D6 соединяется со вторым разрядом произведения (M l). Но тогда первое частное произведение необходимо сдвинуть на один разряд влево по отношению ко второму частному произведению!

Это арифметическое действие выполняется за счет того, что младший разряд группы входов А соединяется с первым разрядом частного произведения, первый разряд группы входов А соединяется со вторым разрядом частного произведения, и т. д. Однако старший разряд группы входов А не с чем соединять!

Для того чтобы разрешить это противоречие вспомним, что если записать слева от числа ноль, то значение исходного числа не изменится, поэтому мы должны этот разряд соединить с общим проводом схемы, добавляя тем самым ноль в старший разряд первого частного произведения.

Точно таким же образом осуществляется суммирование к результату третьего и четвертого частного произведения. Эту операцию выполняют микросхемы D4 и D2 соответственно. Отличие в построении схемы заключается только в том, что здесь не нужно задумываться о старшем разряде предыдущей суммы, ведь предыдущая микросхема сумматора формирует сигнал переноса для последующей микросхемы.

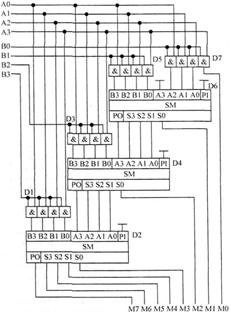
Рисунок 14.12 – Принципиальная схема матричного умножителя 4 на 4

Если внимательно посмотреть на схему умножителя, приведенную на рисунке 14.12, то можно увидеть, что она образует матрицу, сформированную цепями, по которым передаются разряды числа А и числа В. В точках пересечения этих цепей находятся логические элементы "2И". Именно по этой причине умножители, реализованные по данной схеме, получили название матричных умножителей.

Скорость работы схемы, приведенной на рисунке 14.12, определяется максимальным временем распространения сигнала по самому длинному пути. Это путь, проходящий через микросхемы D7, D6, D4, D2. Время работы схемы можно сократить, если сумматоры располагать не последовательно друг за другом, как это предполагается алгоритмом двоичного умножения (пример умножения приведен на рисунке 14.11), а суммировать частичные произведения попарно, затем суммировать пары частичных произведений и т. д. В этом случае время выполнения операции умножения значительно сократится.

Особенно заметен выигрыш в быстродействии при построении многоразрядных умножителей. Однако ничего не бывает бесплатно. В обмен на увеличение быстродействия придется заплатить увеличением разрядности сумматоров, а значит, сложностью схемы. Если сумматоры частных произведений останутся той же разрядности, что и ранее, то разрядность сумматоров пар частичных произведений должна быть увеличена на единицу.

Разрядность сумматоров четверок частичных произведений будет на два разряда больше разрядности сумматоров частичных произведений, т. к. при суммировании четырех чисел их значение в наиболее неблагоприятном случае может увеличиться в четыре раза, и т. д.

Цифровые матричные умножители широко применяются в схемах обработки сигналов для изменения коэффициента передачи устройства, для реализации преобразователей частоты, и как составляющая часть цифровых фильтров.