Рассмотрим подкласс невозможных фигур, изучаемый теорией кос и узлов.

Определим мультибар как многогранник, состоящий из набора брусков прямоугольного сечения, составляющих фигуру правильного многоугольника. (рис.6).

Опишем каждую сторону многогранника как линию косы и применим к ним основные соотношения теории кос: соотношение далекой коммутативности:ac = ca и соотношение сплетения: aba = bab. (рис 7)

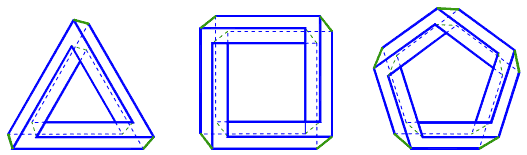
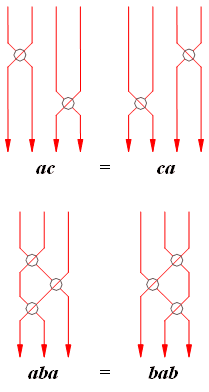
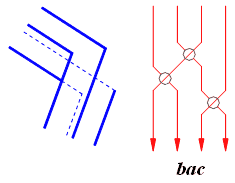
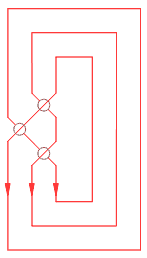
рис.6 рис 7 рис 8 рис.9

Четырехэлементные косы, соответствующие трибару, невозможному квадрату и невозможному пентагону имеют вид: bacbacbac , bacbacbacbac, и bacbacbacbacbac.

Замыкание косы преобразует ее в узел (рис.8, рис.9).

Следовательно, если соединение, соответствующее мультибару, отличается от тривиального четырехэлементного соединения, тогда мультибар является невозможной фигурой.

У теории кос и узлов серьез­ные приложения к комп­лексному анализу, механике и физи­ке элементарных частиц, обнаружились глубокие связи между этой теорией и абстрактной алгеброй. Здесь оказались заме­шаны не только классические раз­делы физики (статистическая физика, напри­мер модель... льда), но и современная квантовая теория. А идея кодирова­ния химической информации в ма­леньких узелках (и косах!) вновь воз­никла в молекулярной биологии при расшифровке аминокислот и изучении ДНК.

Алгебра кос

Узлы и косы можно рассматривать как алгебраические объекты: их можно умножать. Возьмем две косы a и bc одинаковым числом нитей и соединим нижние концы нитей первой косы с верхними концами второй косы; полученную косу, сжатую в два раза в вертикальном направлении, называют произведением этих двух кос и обозначают ab.

Умножение ассоциативно, т.е. для любых трех кос a, b, c косы (a∙b) ∙c и a∙ (b∙c) эквивалентны. Тривиальная коса играет роль единицы. Чтобы получить обратную косу (т.е. a^-1), нужно зеркально отразить косу a относительно горизонтальной плоскости. Умножение кос некоммутативно.

Иными словами, косы образуют группу. Эта группа некоммутативна.

Прямолинейные и топологические симплексы. Примеры.

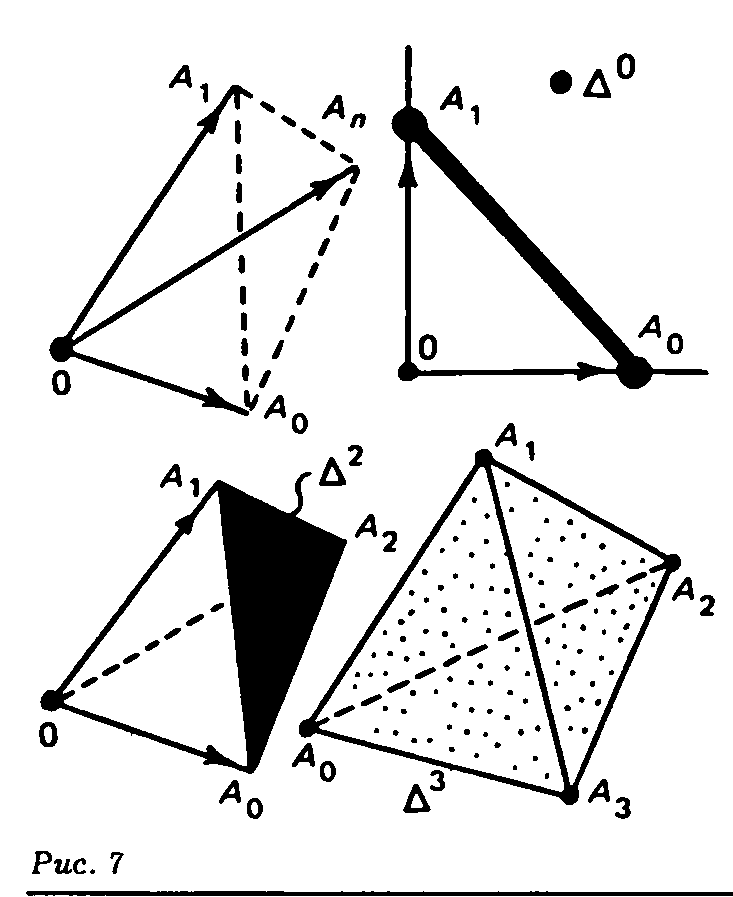
Симплекс является выпуклой линейной оболочкой точек . Поэтому он иногда называется прямолинейным( или евклидовым) симплексом.

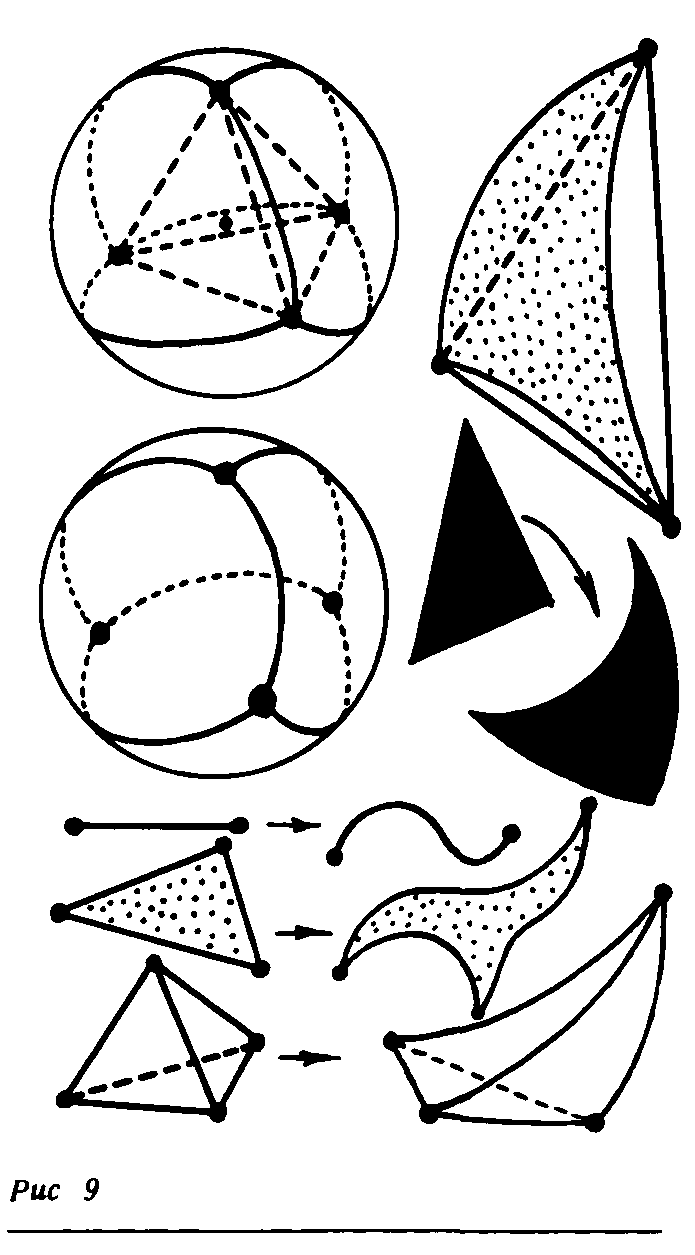
Вопрос 38. Международное сравнительное мониторинговое исследование качества математического и естественнонаучного образования TIMSS.

Международное мониторинговое исследование качества школьного математического и естественнонаучного образования TIMSS(англ. TIMSS — Trends in Mathematics and Science Study) — это программа, организованная Международной ассоциацией по оценке учебных достижений IEA. Данное исследование позволяет сравнить уровень и качество математического и естественнонаучного образования учащихся 4-х классов начальной школы и учащихся 8-х классов в различных странах мира, а также выявить различия в национальных системах образования.

Исследование проводится циклично — один раз в четыре года, и к настоящему времени было проведено шесть раз: в 1995, 1999, 2003, 2007, 2011 и 2015 годах.

При этом трижды с 1995 года (последний раз в 2015 году) проводилось «расширенное» исследование (Advanced TIMSS), включающее в себя изучение достижений обучающихся последнего класса школы (в России это 11-й, в США — 12-й и т. д.)

Краткая информация об исследовании TIMSS

Основной целью международного исследования TIMSS является сравнительная оценка качества математического и естественнонаучного образования в начальной и основной школе. Каждые четыре года оцениваются образовательные достижения учащихся 4 и 8 классов, включающие не только их знания и умения, но и отношения к предметам, интересы и мотивации к обучению. Исследование спланировано таким образом, что его результаты позволяют отслеживать тенденции в математическом и естественнонаучном образовании участвующих стран каждые 4 года, когда учащиеся 4 классов становятся учащимися 8 класса. Таким образом, осуществляется мониторинг учебных достижений учащихся начальной и основной школы, а также изменений, происходящих в математическом и естественнонаучном образовании при переходе из начальной в основную школу.

Дополнительно изучаются особенности содержания школьного математического и естественнонаучного образования в странах-участницах исследования, особенности учебного процесса, а также факторы, связанные с характеристиками образовательных учреждений, учителей, учащихся и их семей. Для этого дополнительно к международному тестированию проводится анкетирование учащихся, учителей и администрации школ, участвовавших в исследовании. Полученные данные позволяют выявить факторы, влияющие на результаты тестирования, и объяснить состояние математического и естественнонаучного образования в странах-участницах исследования.

В проведении исследования и разработке его инструментария принимают участие многие научно-исследовательские центры и профессиональные организации мира.

В России данное исследование осуществляется Центром оценки качества образования Института содержания и методов обучения Российской академии образования(ИСМО РАО) при активном участии Министерства образования и науки РФ и органов управления образованием регионов.

Характеристика инструментария исследования

В качестве основы для разработки инструментария исследования TIMSS используется специальный рамочный документ «TIMSS Assessment Frameworks and Specifications», в котором определены общие подходы к оценке образовательных достижений по математике и естествознанию, разработке тестов и тестовых заданий, описано проверяемое содержание по математике и естествознанию, а также виды познавательной деятельности, которые должны продемонстрировать учащиеся при выполнении заданий, перечислены основные факторы, характеризующие учащихся, учителей и образовательные учреждения, для анализа которых собирается информация в процессе анкетирования, приведены примеры заданий.

Инструментарий международного исследования TIMSS включает:

тесты достижений;

анкеты (для учащихся, учителей, администрации образовательного учреждения, экспертов в области образования, наблюдателей за качеством исследования);

методическое обеспечение (руководство для национальных координаторов по организации и проведению исследования, руководство по формированию выборки, руководство для школьных координаторов, руководство по проведению тестирования, руководства по проверке заданий со свободными ответами, руководство по вводу данных и др.);

программное обеспечение (по отбору классов и учащихся, по вводу данных).

Международные тесты разрабатываются на основе следующих принципов:

адекватный охват проверяемого содержания и видов учебно-познавательной деятельности;

максимальное соответствие содержания международных тестов изучаемому материалу в большинстве стран-участниц;

обеспечение связи тестов;

значимость проверяемого содержания с точки зрения развития математического и естественнонаучного образования;

соответствие возрастным особенностям учащихся, для оценки достижений которых разрабатывался тест;

соответствие требованиям, предъявляемым к массовым исследованиям.

Для оценки математической и естественнонаучной подготовки учащихся в тесты (в каждый вариант) включаются задания и по математике, и по естествознанию. Используются задания разного типа (с выбором ответа, с кратким и полным развернутым ответом, практические задания).

Вопрос 39. Международное исследование образовательных достижений PISA

Международная программа по оценке образовательных достижений учащихся PISA (Programme for International Student Assessment) является мониторинговым исследованием качества общего образования, которое отвечает на вопрос «Обладают ли учащиеся 15-летнего возраста, получившие обязательное общее образование, знаниями и умениями, необходимыми им для полноценного функционирования в современном обществе, т.е. для решения задач в различных сферах человеческой деятельности, общения и социальных отношений?». Данная программа осуществляется Организацией Экономического Сотрудничества и Развития (OECD). Исследование проводится трехлетними циклами, начиная с 2000 года.

В исследовании PISA оценка образовательных достижений обучающихся проводится по следующим трем основным направлениям: «грамотность чтения» (это способность человека к осмыслению письменных текстов, к использованию их содержания для достижения собственных целей, развития знаний), «математическая грамотность» (это способность индивидуума формулировать, применять и интерпретировать математику в разнообразных контекстах. Включает математические рассуждения, использование матем. понятий, методов), «естественнонаучная грамотность» (способность человека занимать активную гражданскую позицию по вопросам, связанным с естественными науками), а также по дополнительным направлениям «финансовая грамотность» и «решение проблем», в рамках которых особое внимание уделяется оценке овладения обучающимися общеучебными и интеллектуальными умениями.

В исследовании 2015 года основное внимание уделялось естественнонаучной грамотности и выявлению тенденций развития естественнонаучного образования в мире за последние годы.

Исследование PISA позволяет выявить и сравнить изменения, происходящие в системах образования в разных странах и оценить эффективность стратегических решений в области образования. Число стран, охваченных программой исследования, постепенно увеличивается.

Для реализации программы исследования разработан специальный диагностический инструментарий, который состоит из блока тестовых заданий, включающих в себя закрытые и открытые задания по математике, естественнонаучным дисциплинам, пониманию текстов и других видов информации. Некоторые задания состоят из нескольких вопросов различного уровня сложности, которые относятся к одной и той же ситуации.

Отличительной характеристикой исследования является его направленность на практические умения обучающихся применять теоретические знания и навыки в жизненных ситуациях, несвязанных непосредственно с учебными предметами. Обучающиеся вовлекаются в проблемы, с которыми они встречаются в реальной жизни, выполняют задания, требующие от них комплексного мышления, планирования и оценки, решают проблемы, аргументируют выбор их решения и т.д.

Основная задача исследования PISA - анализ реальных результатов, полученных в рамках объективных измерений на основе инструментария, отражающего мировые приоритеты в области образования, и извлечение из них научно обоснованных и созидательных для образовательной политики выводов.