Ращательное движение твердого тела вокруг оси. Угловая скорость и угловое ускорение
Вращательным движением твердого тела вокруг неподвижнойосиназывается такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными (рис.13).
Проходящая через неподвижные точки А и В прямая АВ называется осью вращения.
Так как расстояния между точками твердого тела должны оставаться неизменными, то очевидно, что при вращательном движении все точки, принадлежащие оси вращения, будут неподвижны, а все остальные точки тела будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси.
Для определения положения вращающегося тела проведем через ось вращения, вдоль которой направим ось 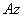 , полуплоскость - неподвижную и полуплоскость, врезанную в само тело и вращающуюся вместе с ним (рис. 13).
, полуплоскость - неподвижную и полуплоскость, врезанную в само тело и вращающуюся вместе с ним (рис. 13).
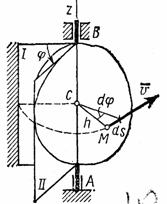
Рис.13
Тогда положение тела в любой момент времени однозначно определится взятым с соответствующим знаком углом 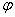 между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол
между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол 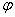 положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси
положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси 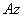 ), и отрицательным, если по ходу часовой стрелки. Измерять угол
), и отрицательным, если по ходу часовой стрелки. Измерять угол 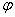 будем всегда в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла
будем всегда в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла 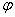 от времени t, т.е.
от времени t, т.е.
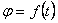 .
.
Уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси.
Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость  и угловое ускорение
и угловое ускорение 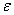 .
.
Если за промежуток времени 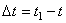 тело совершает поворот на угол
тело совершает поворот на угол 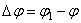 , то численно средней угловой скоростью тела за этот промежуток времени будет
, то численно средней угловой скоростью тела за этот промежуток времени будет 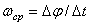 . В пределе при
. В пределе при 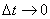 найдем, что
найдем, что
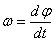 или
или 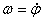 .
.
Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени. Знак  определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки,
определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки,  >0, а когда по ходу часовой стрелки, то
>0, а когда по ходу часовой стрелки, то  <0.
<0.
Размерность угловой скорости 1/Т (т.е. 1/время); в качестве единицы измерения обычно применяют рад/с или, что тоже, 1/с (с-1), так как радиан - величина безразмерная.
Угловую скорость тела можно изобразить в виде вектора 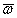 , модуль которого равен |
, модуль которого равен | 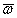 | и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.14). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
| и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.14). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
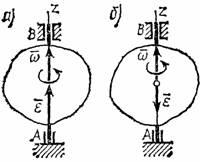
Рис.14
Угловое ускорение характеризует изменение с течением времени угловой скорости тела. Если за промежуток времени 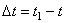 угловая скорость тела изменяется на величину
угловая скорость тела изменяется на величину 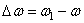 , то числовое значение среднего углового ускорения тела за этот промежуток времени будет
, то числовое значение среднего углового ускорения тела за этот промежуток времени будет 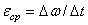 . В пределе при
. В пределе при 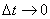 найдем,
найдем,
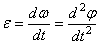 или
или 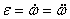 .
.
Таким образом, числовое значение углового ускорения, тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела по времени.
Размерность углового ускорения 1/T2 (1/время2); в качестве единицы измерения обычно применяется рад/с2 или, что то же, 1/с2 (с-2).
Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает, - замедленным. Легко видеть, что вращение будет ускоренным, когда величины  и
и 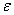 имеют одинаковые знаки, и замедленным, - когда разные.
имеют одинаковые знаки, и замедленным, - когда разные.
Угловое ускорение тела (по аналогии с угловой скоростью) можно также изобразить в виде вектора 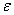 , направленного вдоль оси вращения. При этом
, направленного вдоль оси вращения. При этом
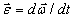 .
.
Направление 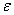 совпадает с направлением
совпадает с направлением  , когда тело вращается ускоренно и (рис.14,а), противоположно
, когда тело вращается ускоренно и (рис.14,а), противоположно  при замедленном вращении (рис.14,б).
при замедленном вращении (рис.14,б).
34. Скорости и ускорения точек вращающегося тела.
Установив характеристики движения всего тела в целом, перейдем к изучению движения отдельных его точек.
1. Скорости точек тела. Рассмотрим какую-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения (см. рис.13). При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время 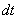 происходит элементарный поворот тела на угол
происходит элементарный поворот тела на угол 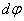 , то точка М при этом совершает вдоль своей траектории элементарное перемещение
, то точка М при этом совершает вдоль своей траектории элементарное перемещение 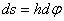 . Тогда числовое значение скорости точки будет равно отношению
. Тогда числовое значение скорости точки будет равно отношению 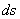 к
к 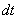 , т.е
, т.е
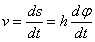 или
или 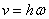 .
.
Скорость 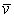 в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.
в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.
Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения.
Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М.
Так как для всех точек тела  имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.
имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.
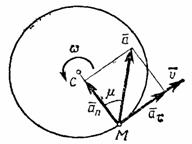
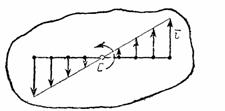
Рис.15 Рис. 16
2. Ускорения точек тела. Для нахождения ускорения точки М воспользуемся формулами 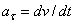 ,
, 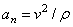 .
.
В нашем случае 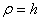 . Подставляя значение
. Подставляя значение 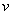 в выражения
в выражения 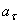 и
и 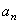 , получим:
, получим:
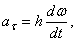
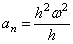
или окончательно:
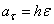 ,
, 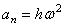 .
.
Касательная составляющая ускорения 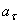 направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при, замедленном); нормальная составляющая
направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при, замедленном); нормальная составляющая 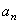 всегда направлена по радиусу МС к оси вращения (рис.16). Полное ускорение точки М будет
всегда направлена по радиусу МС к оси вращения (рис.16). Полное ускорение точки М будет 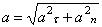 или
или 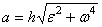 .
.
Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом 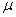 , который вычисляется по формуле
, который вычисляется по формуле 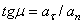 . Подставляя сюда значения
. Подставляя сюда значения 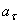 и
и 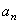 , получаем
, получаем 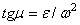 .
.
Так как  и
и 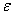 имеют в данный момент времени для всех точек тела одно и то же значение, то ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол
имеют в данный момент времени для всех точек тела одно и то же значение, то ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол 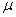 с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис.18.
с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис.18.
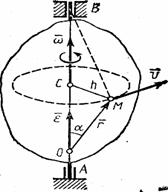
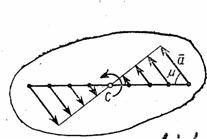
Рис.17 Рис.18
3. Векторы скорости и ускорения точек тела. Чтобы найти выражения непосредственно для векторов 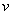 и
и 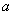 , проведем из произвольной точки О оси АВ радиус-вектор
, проведем из произвольной точки О оси АВ радиус-вектор 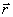 точки М (рис. 17). Тогда
точки М (рис. 17). Тогда 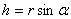 и по формуле
и по формуле
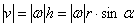 или
или 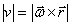 .
.
Таким образом, модуль векторного произведения 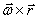 равен модулю скорости точки М. Направления векторов
равен модулю скорости точки М. Направления векторов 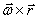 и
и 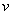 тоже совпадают (оба они перпендикулярны плоскости ОМВ) и размерности их одинаковы. Следовательно,
тоже совпадают (оба они перпендикулярны плоскости ОМВ) и размерности их одинаковы. Следовательно, 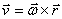 - формула Эйлера, т.е. вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки.
- формула Эйлера, т.е. вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки.
.35. авномерное и равнопеременное вращения
Если угловая скорость тела остается во все время движения постоянной (  =const), то вращение тела называется равномерным. Найдем закон равномерного вращения. Из формулы
=const), то вращение тела называется равномерным. Найдем закон равномерного вращения. Из формулы 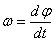 имеем
имеем 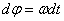 .
.
Отсюда, считая, что в начальный момент времени t=0 угол 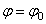 , и беря интегралы слева от
, и беря интегралы слева от 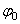 до
до 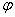 , а справа от 0 до t, получим окончательно
, а справа от 0 до t, получим окончательно
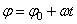 .
.
Из равенства следует, что при равномерном вращении, когда 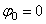
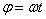 и
и 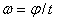 .
.
В технике скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину через n об/мин. Найдем зависимость между n об/мин и  1/с. При одном обороте тело повернется на угол
1/с. При одном обороте тело повернется на угол 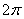 , а при n оборотах на
, а при n оборотах на 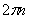 ; этот поворот делается за время t = 1 мин = 60 сек. Из равенства следует тогда, что
; этот поворот делается за время t = 1 мин = 60 сек. Из равенства следует тогда, что
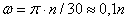 .
.
Если угловое ускорение тела во все время движения остается постоянным 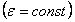 , то вращение называется равнопеременным. Найдем закон равнопеременного вращения, считая, что в начальный момент времени t=0 угол
, то вращение называется равнопеременным. Найдем закон равнопеременного вращения, считая, что в начальный момент времени t=0 угол 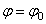 , а угловая скорость
, а угловая скорость 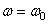 (
( 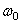 -начальная угловая скорость).
-начальная угловая скорость).
Из формулы 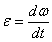 имеем
имеем 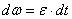 . Интегрируя левую часть в пределах от
. Интегрируя левую часть в пределах от 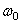 до
до  , а правую - в пределах от 0 до t, найдем
, а правую - в пределах от 0 до t, найдем 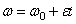 ,
,
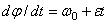 или
или 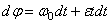 .
.
Вторично интегрируя, найдем отсюда закон равнопеременного вращения
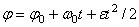 .
.
Если величины  и
и 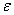 имеют одинаковые знаки, то вращение будет равноускоренным, а если разные - равнозамедленным.
имеют одинаковые знаки, то вращение будет равноускоренным, а если разные - равнозамедленным.
36.Передаточные механизмы. В технике таких механизмов огромное разнообразие и количество. В общем случае их называют передаточными механизмами.
С помощью передаточных механизмов вращение тела с одной угловой скоростью преобразовывают во вращение другого тела с иной угловой скоростью. А возможно, и в ином направлении. Используются фрикционные (за счет трения), ременные, цепные, зубчатые, червячные и иные передачи. Для значительного изменения угловой скорости используются редукторы.
Решая задачи кинематики, необходимо научиться быстро и правильно находить угловые скорости связанных между собой тел, скорости и ускорения отдельных точек тел.
Некоторые виды передач схематично представлены на плакате 10к. Здесь же мы рассмотрим простейший случай передачи вращения от одного вращающегося тела другому.

Отношение угловой скорости ведущего вала к угловой скорости ведомого ( выходного ) вала принято называть передаточным отношением.

Кинематические расчеты в передаточных механизмах весьма просты
37. Сложное движение точки. Относительное, переносное и абсолютное движения.
До сих пор мы изучали движение точки или тела по отношению к одной заданной системе отсчета. Однако в ряде случаев при решении задач механики оказывается целесообразным (а иногда и необходимым) рассматривать движение точки (или тела) одновременно по отношению к двум системам отсчета, из которых одна считается основной или условно неподвижной, а другая определенным образом движется по отношению к первой. Движение, совершаемое при этом точкой (или телом), называют составным или сложным. Например, шар, катящийся по палубе движущегося парохода, можно считать совершающим по отношению к берегу сложное движение, состоящее из качения по отношению к палубе (подвижная система отсчета), и движение вместе с палубой парохода по отношению к берегу (неподвижная система отсчета). Таким путем сложное движение шара разлагается на два более простых и более легко исследуемых.
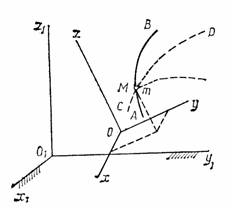
Рис.48
Рассмотрим точку М, движущуюся по отношению к подвижно системе отсчета Oxyz, которая в свою очередь как-то движется относительно другой системы отсчета 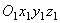 , которую называем основной или условно неподвижной (рис. 48). Каждая из этих систем отсчета связана, конечно, с определенным телом, на чертеже не показанным. Введем следующие определения.
, которую называем основной или условно неподвижной (рис. 48). Каждая из этих систем отсчета связана, конечно, с определенным телом, на чертеже не показанным. Введем следующие определения.
1. Движение, совершаемое точкой М по отношению к подвижной системе отсчета (к осям Oxyz), называется относительнымдвижением (такое движение будет видеть наблюдатель, связанный с этими осями и перемещающийся вместе с ними). Траектория АВ, описываемая точкой в относительном движении, называется относительной траекторией. Скорость точки М по отношению к осям Oxyzназывается относительной скоростью (обозначается 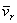 ), a ускорение - относительным ускорением (обозначается
), a ускорение - относительным ускорением (обозначается 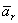 ). Из определения следует, что при вычислении
). Из определения следует, что при вычислении 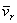 и
и 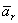 можно движение осей Oxyz во внимание не принимать (рассматривать их как неподвижные).
можно движение осей Oxyz во внимание не принимать (рассматривать их как неподвижные).
2. Движение, совершаемое подвижной системой отсчета Oxyz (и всеми неизменно связанными с нею точками пространства) по отношению к неподвижной системе 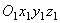 , является для точки М переносным движением.
, является для точки М переносным движением.
Скорость той неизменно связанной с подвижными осями Oxyz точки m, с которой в данный момент времени совпадает движущаяся точка М, называется переносной скоростью точки М в этот момент (обозначается 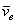 ), а ускорение этой точки m - переносным ускорением точки М (обозначается
), а ускорение этой точки m - переносным ускорением точки М (обозначается 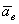 ). Таким образом,
). Таким образом,
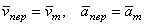 .
.
Если представить себе, что относительное движение точки происходит по поверхности (или внутри) твердого тела, с которым жестко связаны подвижные оси Oxyz, то переносной скоростью (или ускорением) точки М в данный момент времени будет скорость (или ускорение) той точки т тела, с которой в этот момент совпадает точка М.
3. Движение, совершаемое точкой по отношению к неподвижной системе отсчета 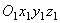 , называется абсолютным или сложным. Траектория CD этого движения называется абсолютной траекторией, скорость - абсолютной скоростью (обозначается
, называется абсолютным или сложным. Траектория CD этого движения называется абсолютной траекторией, скорость - абсолютной скоростью (обозначается 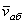 ) и ускорение - абсолютным ускорением (обозначается
) и ускорение - абсолютным ускорением (обозначается 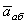 ).
).
В приведенном выше примере движение шара относительно палубы парохода будет относительным, а скорость - относительной скоростью шара; движение парохода по отношению к берегу будет для шара переносным движением, а скорость той точки палубы, которой в данный момент времени касается шар будет в этот момент его переносной скоростью; наконец, движение шара по отношению к берегу будет его абсолютным движением, а скорость - абсолютной скоростью шара.
При исследовании сложного движения точки полезно применять «Правило остановки». Для того, чтобы неподвижный наблюдатель увидел относительное движение точки, надо остановить переносное движение.
Тогда будет происходить только относительное движение. Относительное движение станет абсолютным. И наоборот, если остановить относительное движение, переносное станет абсолютным и неподвижный наблюдатель увидит только это переносное движение.
В последнем случае, при определении переносного движения точки, обнаруживается одно очень важное обстоятельство. Переносное движение точки зависит от того в какой момент будет остановлено относительное движение, от того, где точка находится на среде в этот момент. Так как, вообще говоря, все точки среды движутся по-разному. Поэтому логичнее определять переносное движение точки как абсолютное движение той точки среды, с которой совпадает в данный момент движущаяся точка.
38. Teopeмa сложения скоростей.
Пусть некоторая точка М совершает движение по отношению к системе отсчета Oxyz, которая сама движется произвольным образом по отношению к неподвижной системе отсчета 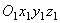 , (рис.49).
, (рис.49).
Конечно, абсолютное движение точки М определяется уравнениями
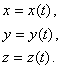
Относительное движение – в движущихся осях уравнениями
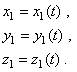
|
Уравнений, определяющих переносное движение точки, не может быть вообще. Так как, по определению, переносное движение точки М – это движение относительно неподвижных осей той точки системы 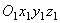 , с которой совпадает точка в данный момент. Но все точки подвижной системы движутся по-разному.
, с которой совпадает точка в данный момент. Но все точки подвижной системы движутся по-разному.
Положение подвижной системы отсчета может быть также определено, если задать положение точки О радиусом-вектором 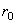 , проведенным из начала неподвижной системы отсчета, и направления единичных векторов
, проведенным из начала неподвижной системы отсчета, и направления единичных векторов 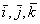 подвижных осей Оx, Oy, Oz.
подвижных осей Оx, Oy, Oz.
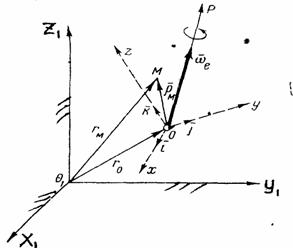
Рис.49
Произвольное переносное движение подвижной системы отсчета слагается из поступательного движения со скоростью 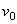 точки О и движения вокруг мгновенной оси вращения ОР, походящей через точку О, с мгновенной угловой скоростью
точки О и движения вокруг мгновенной оси вращения ОР, походящей через точку О, с мгновенной угловой скоростью 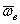 . Вследствие переносного движения подвижной системы отсчета радиус-вектора
. Вследствие переносного движения подвижной системы отсчета радиус-вектора 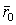 и направления единичных векторов
и направления единичных векторов 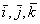 изменяются. Если векторы
изменяются. Если векторы 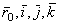 заданы в функции времени, то переносное движение подвижной системы отсчета вполне определено.
заданы в функции времени, то переносное движение подвижной системы отсчета вполне определено.
Положение точки М по отношению к подвижной системе отсчета можно определить радиусом-вектором 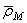
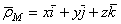 ,
,
где координаты x, y, z точки М изменяются с течением времени вследствие движения точки М относительно подвижной системы отсчета. Если радиус-вектор 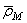 задан в функции времени, то относительное движение точки М, т.е. движение этой точки относительно подвижной системы отсчета, задано.
задан в функции времени, то относительное движение точки М, т.е. движение этой точки относительно подвижной системы отсчета, задано.
Положение точки М относительно неподвижной системы отсчета 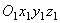 , может быть определено радиусом-вектором
, может быть определено радиусом-вектором 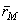 . Из рис.49 видно, что
. Из рис.49 видно, что
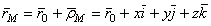 . (1)
. (1)
Если относительные координаты x,y,z точки М и векторы 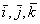 определены в функции времени, то слагающееся из относительного и переносного движений составное движение точки М, т.е. движение этой точки по отношению к неподвижной системе отсчета, также надо считать заданным.
определены в функции времени, то слагающееся из относительного и переносного движений составное движение точки М, т.е. движение этой точки по отношению к неподвижной системе отсчета, также надо считать заданным.
Скорость составного движения точки М, или абсолютная скорость этой точки, равна, очевидно, производной от радиуса-вектора 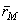 точки M по времени t
точки M по времени t
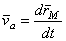 .
.
Поэтому, дифференцируя равенство (1) по времени t, получим
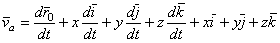 . (2)
. (2)
Разобьем слагаемые в правой части этого равенства на две группы по следующему признаку. К первой группе отнесем те слагаемые, которые содержат производные только от относительных координат x,y,z, а ко второй - те слагаемые, которые содержат производные от векторов 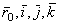 , т.е. от величин, изменяющихся только вследствие переносного движения подвижной системы отсчета
, т.е. от величин, изменяющихся только вследствие переносного движения подвижной системы отсчета
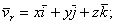 (3)
(3)
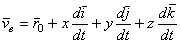 . (4)
. (4)
Каждая из групп слагаемых, обозначенных через 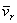 и
и 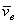 , представляет собой, по крайней мере, по размерности некоторую скорость. Выясним физический смысл скоростей
, представляет собой, по крайней мере, по размерности некоторую скорость. Выясним физический смысл скоростей 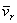 и
и 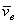 .
.
Скорость 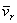 , как это следует из равенства (3), вычисляется в предположении, что изменяются только относительные координаты x,y,zточки М, но векторы
, как это следует из равенства (3), вычисляется в предположении, что изменяются только относительные координаты x,y,zточки М, но векторы 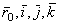 остаются постоянными, т.е. подвижная система отсчета Oxyz как бы условно считается неподвижной. Итак, скорость
остаются постоянными, т.е. подвижная система отсчета Oxyz как бы условно считается неподвижной. Итак, скорость 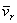 представляет собой относительную скорость точки М.
представляет собой относительную скорость точки М.
Скорость 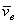 вычисляется так, как будто бы точка М не двигалась относительно подвижной системы отсчета, так как производные x,y,zв равенство (4) не входят. Поэтому скорость
вычисляется так, как будто бы точка М не двигалась относительно подвижной системы отсчета, так как производные x,y,zв равенство (4) не входят. Поэтому скорость 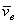 представляет собой переносную скорость точки М.
представляет собой переносную скорость точки М.
Итак, 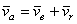 . (5)
. (5)
Это равенство выражает теорему сложения скоростей в случае, когда переносное движение является произвольным: абсолютная скорость точки М равна геометрической сумме переносной и относительной скоростей этой точки.
Пример 13. Колечко М движется по вращающемуся стержню так, что 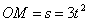 (см) и
(см) и 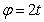 (рад).
(рад).
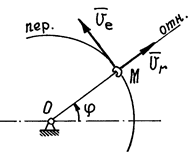
Рис.50
Ранее было установлено, что траектория относительного движения – прямая линия, совпадающая со стержнем, и движение это определяется уравнением 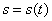 . Траектория переносного движения точки М в момент времени t – окружность радиуса
. Траектория переносного движения точки М в момент времени t – окружность радиуса 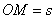 .
.
Поэтому относительная скорость 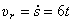
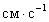 . И направлена по касательной к траектории вдоль стержня (рис.50). Переносная скорость колечка, как при вращении вокруг оси,
. И направлена по касательной к траектории вдоль стержня (рис.50). Переносная скорость колечка, как при вращении вокруг оси, 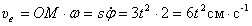 . Направлен вектор этой скорости по касательной к траектории переносного движения, перпендикулярно стержню.
. Направлен вектор этой скорости по касательной к траектории переносного движения, перпендикулярно стержню.
Абсолютная скорость колечка 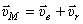 . Величина ее, т.к.
. Величина ее, т.к. 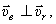
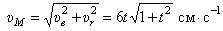 .
.
39. Теорема сложения ускорений. Ускорение Кориолиса.
Ускорение составного движения точки М, или абсолютное ускорение этой точки, равно, очевидно, производной от абсолютной скорости точки М по времени t
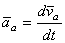
Поэтому, дифференцируя равенство по времени, получим
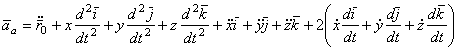 .
.
Разделим слагаемые правой части этого равенства на три группы.
К первой группе отнесем слагаемые, содержащие только производные от относительных координат x,y и z, но не содержащие производные от векторов 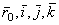 :
:
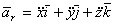 .
.
Ко второй группе отнесем слагаемые, которые содержат только производные от векторов 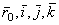 , но не содержащие производных от относительных координат x,y,z:
, но не содержащие производных от относительных координат x,y,z:
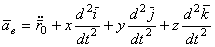 .
.
Осталась еще одна группа слагаемых, которые не могли быть отнесены ни к первой, ни ко второй, так как они содержат производные от всех переменных x, y, z, 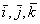 . Обозначим эту группу слагаемых через
. Обозначим эту группу слагаемых через 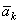 :
:
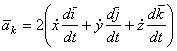 .
.
Каждая из выделенных групп представляет собой, по крайней мере по размерности, некоторое ускорение. Выясним физический смысл всех трех ускорений: 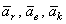 .
.
Ускорение 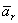 , как это видно из равенства, вычисляется так, как если бы относительные координаты x,y,z изменялись с течением времени, а векторы
, как это видно из равенства, вычисляется так, как если бы относительные координаты x,y,z изменялись с течением времени, а векторы 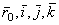 оставались неизменными, т.е. подвижная система отсчета Oxyz как бы покоилась, а точка М двигалась. Поэтому ускорение
оставались неизменными, т.е. подвижная система отсчета Oxyz как бы покоилась, а точка М двигалась. Поэтому ускорение 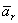 представляет собой относительное ускорение точки М. Так как ускорение (и скорость) относительного движения вычисляется в предположении, что подвижная система отсчета находится а покое, то для определения относительного ускорения (и скорости) можно пользоваться всеми правилами, изложенными ранее в кинематике точки.
представляет собой относительное ускорение точки М. Так как ускорение (и скорость) относительного движения вычисляется в предположении, что подвижная система отсчета находится а покое, то для определения относительного ускорения (и скорости) можно пользоваться всеми правилами, изложенными ранее в кинематике точки.
Ускорение 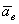 , как это видно из равенства, вычисляется в предположении, что сама точка М покоится по отношению к подвижной системе отсчета Oxyz (x =const, y =const, z =const) и перемещается вместе с этой системой отсчета по отношению к неподвижной системе отсчета
, как это видно из равенства, вычисляется в предположении, что сама точка М покоится по отношению к подвижной системе отсчета Oxyz (x =const, y =const, z =const) и перемещается вместе с этой системой отсчета по отношению к неподвижной системе отсчета 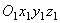 . Поэтому ускорение
. Поэтому ускорение 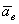 представляет собой переносное ускорение точки М.
представляет собой переносное ускорение точки М.
Третья группа слагаемых определяет ускорение 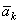 , которое не может быть отнесено не к относительному ускорению
, которое не может быть отнесено не к относительному ускорению 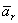 , так как содержит в своем выражении производные
, так как содержит в своем выражении производные 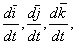 не к переносному ускорению
не к переносному ускорению 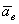 , так как содержит в своем выражении производные
, так как содержит в своем выражении производные 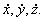
Преобразуем правую часть равенства, припомнив, что
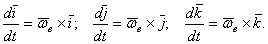
Подставляя эти значения производных в равенства, получим
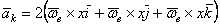
или 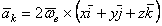 .
.
Здесь вектор 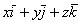 есть относительная скорость
есть относительная скорость 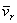 точки М, поэтому
точки М, поэтому
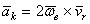 .
.
Ускорение 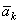 называют ускорением Кориолиса. Ввиду того, что ускорение Кориолиса появляется в случае вращения подвижной системы отсчета, его называют еще поворотным ускорением.
называют ускорением Кориолиса. Ввиду того, что ускорение Кориолиса появляется в случае вращения подвижной системы отсчета, его называют еще поворотным ускорением.
С физической точки зрения появление поворотного ускорения точки объясняется взаимным влиянием переносного и относительного движений.
Итак, ускорение Кориолиса точки равно по модулю и направлению удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки.
Равенство, которое теперь можно сокращенно записать в виде
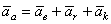 .
.
представляет теорему сложения ускорений в случае, когда переносное движение является произвольным: абсолютное ускорение точки равно векторной сумме переносного, относительного и поворотного ускорений. Эту теорему часто называют теоремой Кориолиса.
Из формулы следует, что модуль поворотного ускорения будет
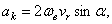
где 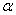 - угол между вектором
- угол между вектором 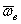 и вектором
и вектором 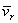 . Чтобы определить направление поворотного ускорения
. Чтобы определить направление поворотного ускорения 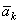 , нужно мысленно перенести вектор
, нужно мысленно перенести вектор 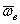 в точку М и руководствоваться правилом векторной алгебры. Согласно этому правилу, вектор
в точку М и руководствоваться правилом векторной алгебры. Согласно этому правилу, вектор 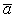 нужно направлять перпендикулярно к плоскости, определяемой векторами
нужно направлять перпендикулярно к плоскости, определяемой векторами 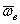 и
и 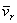 , и так, чтобы, смотря с конца вектора
, и так, чтобы, смотря с конца вектора 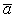 , наблюдатель мог видеть кратчайший поворот от
, наблюдатель мог видеть кратчайший поворот от 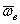 к
к 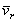 происходящим против движения часовой стрелки (рис. 30).
происходящим против движения часовой стрелки (рис. 30).
Для определения направления 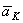 можно также пользоваться следующим правилом Н. Е. Жуковского: чтобы получить направление поворотного ускорения
можно также пользоваться следующим правилом Н. Е. Жуковского: чтобы получить направление поворотного ускорения 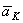 , достаточно составляющую
, достаточно составляющую 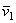 относительной скорости
относительной скорости 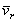 точки М, перпендикулярную к вектору
точки М, перпендикулярную к вектору 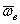 , повернуть (в плоскости, перпендикулярной к вектору
, повернуть (в плоскости, перпендикулярной к вектору 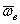 ) на прямой угол вокруг точки М в направлении переносного вращения (рис.51).
) на прямой угол вокруг точки М в направлении переносного вращения (рис.51).
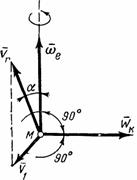
Рис.51
Если переносное движение подвижной системы отсчета есть поступательное движение, то 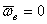 и поэтому поворотное ускорение
и поэтому поворотное ускорение 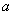 точки также равно нулю. Поворотное ускорение равно, очевидно, нулю и в том случае, когда
точки также равно нулю. Поворотное ускорение равно, очевидно, нулю и в том случае, когда 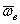 в данный момент времени обращается в нуль.
в данный момент времени обращается в нуль.
Кроме того, поворотное ускорение точки может, очевидно, обращаться в нуль, если:
а) вектор относительной скорости 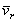 точки параллелен вектору угловой скорости
точки параллелен вектору угловой скорости 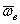 переносного вращения, т.е. относительное движение точки происходит по направлению, параллельному оси переносного вращения;
переносного вращения, т.е. относительное движение точки происходит по направлению, параллельному оси переносного вращения;
б) точка не имеет движения относительно подвижной системы отсчета или относительная скорость 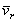 точки в данный момент времени равна нулю (
точки в данный момент времени равна нулю ( 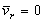 ).
).
Пример 14. Пусть тело вращается вокруг неподвижной оси z. По поверхности его движется точка М (рис. 52). Конечно, скорость этого движения точки – относительная скорость 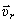 , а скорость вращения тела – угловая скорость переносного движения
, а скорость вращения тела – угловая скорость переносного движения 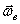 .
.
Ускорение Кориолиса 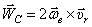 , направлено перпендикулярно этим двум векторам, по правилу направления вектора векторного произведения. Так, как показано на рис. 52.
, направлено перпендикулярно этим двум векторам, по правилу направления вектора векторного произведения. Так, как показано на рис. 52.
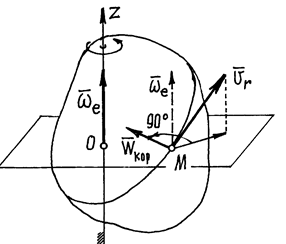
Рис.52
Нетрудно сформулировать более удобное правило определения направления вектора 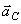 : нужно спроектировать вектор относительной скорости
: нужно спроектировать вектор относительной скорости 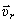 на плоскость перпендикулярную оси переносного вращения и затем повернуть эту проекцию на 90 градусов в плоскости по направлению переносного вращения. Конечное положение проекции вектора
на плоскость перпендикулярную оси переносного вращения и затем повернуть эту проекцию на 90 градусов в плоскости по направлению переносного вращения. Конечное положение проекции вектора 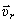 укажет направление кориолисова ускорения. (Это правило было предложено Н.Е. Жуковским).
укажет направление кориолисова ускорения. (Это правило было предложено Н.Е. Жуковским).
40. Ускорения Криолиса. Модуль УскоренияУскорение 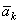 называют ускорением Кориолиса. Ввиду того, что ускорение Кориолиса появляется в случае вращения подвижной системы отсчета, его называют еще поворотным ускорением.
называют ускорением Кориолиса. Ввиду того, что ускорение Кориолиса появляется в случае вращения подвижной системы отсчета, его называют еще поворотным ускорением.
С физической точки зрения появление поворотного ускорения точки объясняется взаимным влиянием переносного и относительного движений.
Итак, ускорение Кориолиса точки равно по модулю и направлению удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки.
Равенство, которое теперь можно сокращенно записать в виде
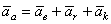 .
.
представляет теорему сложения ускорений в случае, когда переносное д<
