Интерполяция и аппроксимация: соотношение между понятиями и область применения.Возможностипрограммнойсреды MATLAB.

Интерполяция и аппроксимация: соотношение между понятиями и область применения.Возможностипрограммнойсреды MATLAB.

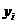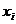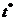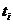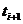На практике часто может возникать необходимость знания значений функции в других точках, отличных от известных значений аргумента . Такая необходимость может иметь место, например, при проведении исследования поведения некоторой системы в моменты времени , находящиеся между значениями и . В свою очередь невозможность получения значений 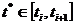обусловлена чаще всего жёсткими условиями на время проведения эксперимента, связанными, как правило, с необходимостью получения большого статического материала (именно в точках ( 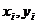)) с целью удовлетворения требованиям точности и достоверности результатов эксперимента.

Задача определения значений 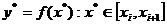решается с помощью аппроксимации – замены функции 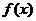некоторой приближенной функцией 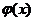таким образом, чтобы отклонение (по некоторому критерию) 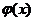от 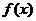было бы наименьшим в заданной области значений аргумента.

Частным случаем аппроксимации является интерполяция, состоящая в следующем: для данной функции 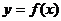строится многочлен 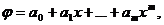принимающий в заданных точках 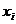те же значения 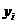, что и функция 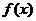, т.е. .

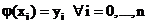При этом предполагается, что среди значений 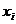нет одинаковых, т.е. 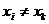при 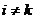. Точки 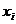называются узлами интерполяции, а многочлен 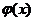– интерполяционным многочленом.

В зависимости от того, сколько полиномов заданной степени используется на всём отрезке интерполяции, различают глобальную и локальную (кусочную) интерполяцию.

Возможностипрограммнойсреды MATLAB:

Цифровая обработка сигналов, изображений и данных:

Финансовый анализ

Анализ и синтез географических карт, включая трёхмерные

Сбор и анализ экспериментальных данных

Взаимодействие с внешними программными продуктами

Финансовый анализ

Анализ и синтез географических карт, включая трёхмерные

Сбор и анализ экспериментальных данных

Взаимодействие с внешними программными продуктами

ФункцияЭйлера: понятие и способывычисления. Теорема Эйлера

Функция Эйлераопределяется для всех целых положительных чиселаи равна количеству чисел ряда 0, 1, …, а-1, взаимно простых са. Обозначением функции Эйлера является j(а).

Например, j(5) = 4, j(6) = 2, j(12) = 4. Иными словами, в соответствии с введенными выше определениями, если 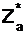– приведенный набор вычетов по модулю а, то .

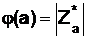Очевидно, что для а = m простого согласно (12)

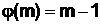. (13)

Функция Эйлера может быть определена исходя из канонического разложения числа вида (1)

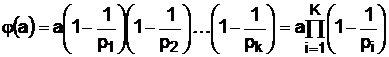, (14)

Или

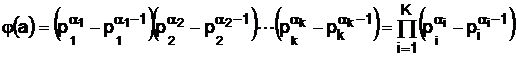. (15)

Например, если а = 60 = 2²×3×5, то согласно (14) имеем:

,

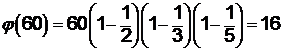либо согласно (15) имеем: .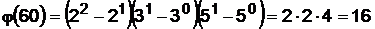

Функция 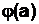является мультипликативной, т.е.

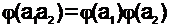(16)

в том случае, если числа a₁ и a₂ взаимно простые.

Из (16), в частности, следует, что, если m = pq, где p и q – простые числа, то, с учётом (13) имеем:

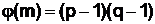. (17)

Теорема Эйлера утверждает, что при m > 1 и 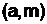= 1 справедливо соотношение

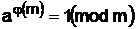, (18)

что также может быть записано как .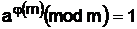

8. Решениесравненияax = 1(modn) с помощью метода цепныхдробейЕвклида.

Известно, что диафантово уравнение имеет решение в том случае, если a>b (в нашем случае n>a), а также если целочисленные коэффициенты a и b являются взаимно простыми (в нашем случае 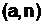= 1).

Уравнение (23) может быть решено на основе метода, базирующегося на разложении отношения 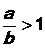в непрерывную дробь с помощью алгоритма Евклида (см. соотношения (2)). Следовательно, для решения сравнения (21) необходимо представить в виде непрерывной (цепной) дроби отношение 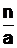. Так, если данное отношение является рациональной несократимой дробью, то её разложение в непрерывную дробь осуществляется по следующей схеме:

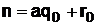, откуда 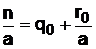; (24)

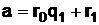, откуда 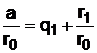; (25)

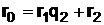, откуда 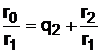; (26)

, ;

, .

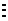
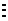
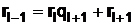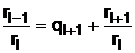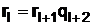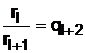Второе слагаемое выражения (24) можно получить из (25):

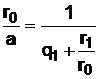. (27)

Тогда, подставляя (26) в (23), получим

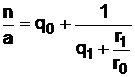. (28)

Далее, по аналогии, отношение 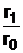в (25) можно, исходя из (26), представить в виде

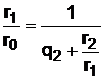. (29)

Подставляя (29) в (28), получим

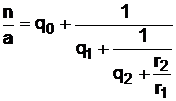. (30)

Действуя далее таким же образом, окончательно получим

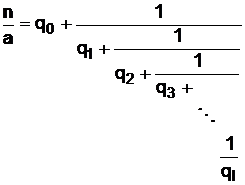. (31)

Числа q₁, q₂, …, участвующие в разложении дроби 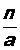в непрерывную, называются неполными частными, а дроби 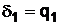, , 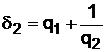, 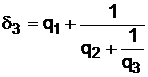… называются подходящими.

Нас в данном случае интересует индекс l при последнем частном цепной дроби, поскольку именно от значения l зависит решение уравнения 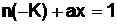. Оно определяется следующим образом:

x= (-1)^l×n_l-1 , (32)

где l – порядок непрерывной дроби, определяющий неполное частное q_l, у которого остаток равен 0 (точнее говоря, в этом случае q_l является полным частным в отличие от других значений q_i).

Коэффициенты n_l, a_l в выражении (31) вычисляются рекурсивно с использованием неполных частных q₁, …, q_l-1 следующим образом.

Так, 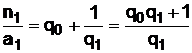, то есть 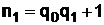, а .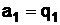

Далее, 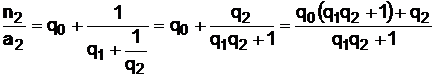, т.е. 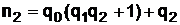, а .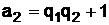

Табличный симплекс-метод

Для упрощения процесса решения исходные данные задачи линейного программирования при решении ее симплекс методом записываются в специальные симплекс-таблицы. Поэтому одна из модификаций симплекс метода получила название табличный симплекс метод. Задача линейного программирования в каноническом виде:

F=a_0,1x₁+a_0,2x₂+...a_0,nx_n +b₀ → max

a_1,1x₁+a_1,2x₂+...a_1,nx_n + x_n+1=b₁

a_2,1x₁+a_2,2x₂+...a_2,nx_n +x_n+2 =b₂

.......................................

a_m,1x₁+a_m,2x₂+...a_m,nx_n+x_n+m=b_m

Исходная таблица для задачи имеет следующий вид:

	x1	x2	...	xn-1	xn	b
F	-a0,1	-a0,2	...	-a0,n-1	-a0,n	-b0
xn+1	a1,1	a1,2	...	a1,n-1	a1,n	b1
xn+2	a2,1	a2,2	...	a2,n-1	a2,n	b2
...	...	...	...	...	...	...
xn+m	am,1	am,2	...	am,n-1	am,n	bm

x₁, x₂, x_n - исходные переменные, x_n+1, x_n+2, x_n+m - дополнительные переменные. Все дополнительные переменные мы приняли как базисные, а исходные переменные как небазисные(дополнительные записаны в первый столбец симплекс-таблицы а исходные в первую строку). При каждой итерации элементы симплекс-таблицы пересчитывают по определеннымправилам.

Алгоритм симплекс-метода.

Подготовительный этап

Приводим задачу ЛП к каноническому виду

F=a_0,1x₁+a_0,2x₂+...a_0,nx_n +b₀ → max

a_1,1x₁+a_1,2x₂+...a_1,nx_n+x_n+1=b₁

a_2,1x₁+a_2,2x₂+...a_2,nx_n+x_n+2=b₂

.......................................

a_m,1x₁+a_m,2x₂+...a_m,nx_n+x_n+m=b_m

В случае если в исходной задаче необходимо найти минимум - знаки коэффициентов целевой функции F меняются на противоположные a_0,n=-a_0,n. Знаки коэффициентов ограничивающих условий со знаком "≥" так же меняются на противоположные. В случае если условие содержит знак "≤" - коэффициенты запишутся без изменений.

Основные операторы ГА

Оператор репродукции (селекции) – искуственная версия естественного отбора, основанного на принципе выживания более приспособленных особей. В результате выполнения этого оператора хромосомы копируются в промежуточную популяцию для дальнейшего «размножения» согласно их значениям фитнесс-функции.

Оператор кроссинговера (скрещивания)­ – основан на принципе наследования потомками генетической информации родителей и определяет передачу признаков (наследственной информации) родителей потомкам.

Оператор мутации – основан на принципе резкого изменения свойств потомков и приобретении у них свойств, отсутствующих у родителей; позволяет повысить разнообразие (изменчивость) особей в популяции (множество решений).

Рисунок 1 – Блок-схема классического (простого) ГА

ПРАКТИКА:

1. Используя программную среду MATLAB, произвестилокальнуюлинейную интерполяцию, а такжеинтерполяцию на основе кубического сплайнафункциональнойзвисимостиy = f(x), представленной рядом значенийxиy:

X -3,5 -2,4 -1,8 0,14 2,12 3,64 5,29 7,72

Y 1,2 2,5 7,3 11,6 12,8 14,9 20,1 24,0.

X -2,5 -1,5 -0,8 1,2 2,53,6 5,7 8,7

Y-3,01,5 2,4 7,6 10,0 14,216,1 20,0.

X -3,4 -2,7 -0,5 0,8 2,0 3,6 4,7 5,7

Y-2,2 -0,5 2,4 5,6 7,0 11,314,1 19,3.

Изобразитьграфикиприближающихфункцийв одной координатной плоскости и определить абсолютную величину разности значений интерполирующей и аппроксимирующей функций в точке x = 2,0.

4. Используя программную среду MATLAB, на основе метода наименьших квадратов с помощью полиномов P_n(x) степени n = 2 иn = 3 подобратьприближённыеаналитическиесоотношения для полученнойэкспериментальнозависимостиy = f(x), представленной рядом значенийxиy:

X -2,5 -1,5 -0,8 1,2 2,53,6 5,5 8,4

Y-3,0-0,5 2,4 7,6 9,1 12,214,2 17,3.

Изобразитьграфикиаппроксимирующихфункцийв одной координатной плоскости и определить абсолютную величину их разности в точке x = 4,0.

5. Получить решение системы сравнений x = 3(mod5), x = 7(mod13), x = 8(mod14) с помощью китайской теоремы об остатках.

6. Используя программную среду MATLAB, получить решениезадачи квадратичного программирования:f(x) = x₁² + 0,5x₂²+ 2x₃²®min, при ограничениях: x₁ + 2x₂ + x₃ – 2 £ 0;

– 2x₁ – x₂ – 3x₃ + 5 £ 0; x₁ –x₂ – 2 £ 0; x₁ + 0,5x₂ – x₃ – 1 £ 0; –x₁ + 2x₂ – 2x₃ + 3 £ 0; x₂ – 3x₃ + 1 £ 0.

7. Получить решение задачи безусловной нелинейной оптимизации: 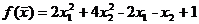®min при начальных значениях переменных x₁(0) = 1; x₂(0) = 1,5 и

заданной точности e£ 0,01. Сопоставить полученное решение с решением при значении e, на порядок большим заданного.

8. Проанализироватьпереопределённую систему линейныхалгебраическихуравнений (СЛАУ) 2,36x₁- 14,0x₂ = -62,8;

3,15x₁- 5,62x₂ = -24,4;

x₁ + 12,5x₂ = 33,5;

-1,08x₁ + 26,0x₂ = 32,8;

-5,73x₁- 5,45x₂ = -47,5

Представить задачу оптимизации в формальном виде, если её вербальная (словесная) формулировка имеет вид: цех производственного предприятия должен изготовить 100 изделий 3-х видов; при этом должно быть изготовлено не менее 20 штук изделий каждого вида; на изготовление изделий каждого вида расходуется 4,0, 3,4 и 2,0 кг металла соответственно при его общем запасе 340,0 кг, а также по 4,75, 11,0 и 2,0 кг пластмассы при её общем запасе 700 кг. Сколько изделий каждого вида необходимо изготовить, чтобы их стоимость была максимальной, если цена одного изделия каждого вида составляет 400, 300 та 200 условных единицсоответственно?

Интерполяция и аппроксимация: соотношение между понятиями и область применения.Возможностипрограммнойсреды MATLAB.

На практике часто может возникать необходимость знания значений функции 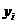в других точках, отличных от известных значений аргумента 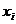. Такая необходимость может иметь место, например, при проведении исследования поведения некоторой системы в моменты времени 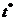, находящиеся между значениям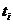и и 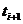. В свою очередь невозможность получения значений 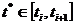обусловлена чаще всего жёсткими условиями на время проведения эксперимента, связанными, как правило, с необходимостью получения большого статического материала (именно в точках ( 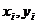)) с целью удовлетворения требованиям точности и достоверности результатов эксперимента.

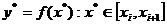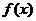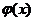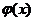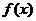Задача определения значений решается с помощью аппроксимации – замены функции некоторой приближенной функцией таким образом, чтобы отклонение (по некоторому критерию) от было бы наименьшим в заданной области значений аргумента.

Частным случаем аппроксимации является интерполяция, состоящая в следующем: для данной функции 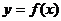строится многочлен 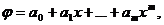принимающий в заданных точках 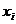те же значения 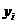, что и функция 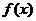, т.е. .

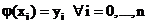При этом предполагается, что среди значений 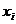нет одинаковых, т.е. 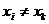при 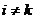. Точки 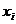называются узлами интерполяции, а многочлен 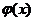– интерполяционным многочленом.

В зависимости от того, сколько полиномов заданной степени используется на всём отрезке интерполяции, различают глобальную и локальную (кусочную) интерполяцию.

Возможностипрограммнойсреды MATLAB:

Цифровая обработка сигналов, изображений и данных:

Финансовый анализ