Сущность и условия применения теории вероятностей.

Тео́риявероя́тностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

При научном исследовании различных физических и технических задач часто приходится встречаться с особого типа явлениями, которые принято называть случайными. Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.

Теория вероятностей занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним или невозможным. Согласно П.Лапласу, внесшему, пожалуй, наибольший вклад в развитие теории вероятностей, она "по существу представляет собой не что иное, как здравый смысл, сведенный к вычислениям". Слово "вероятно", его синонимы и производные от него могут употребляться в различных значениях. Примерами некоторых из них являются следующие утверждения: "Возможно, завтра будет дождь", "Вероятно, теория естественного отбора Дарвина верна" и "Если я брошу монету 100 раз, то, вероятно, что она выпадет вверх "орлом" от 40 до 60 раз". Математическая теория вероятностей имеет дело с утверждениями, аналогичными последнему.

Теория вероятностей является одной из важнейших и необходимых составных частей математики. Методы теории вероятностей широко применяются в различных отраслях естество­знания и техники: в теории надёжности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдения, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках. Теория вероятностей служит также для обоснования математической и прикладной статистики, которые, в свою очередь, используются при планировании и организации производства, при анализе техноло­гических процессов, предупредительном и приёмочном контроле качества продукции и для многих других целей. В последние годы методы теории вероятностей всё шире и шире проникают в различ­ные области науки, техники и экономики, способствуя их прогрессу.

Основные понятия теории вероятностей.

• Событием называется любой исход опыта, различают следующие виды событий:

- случайные

- достоверные

- невозможные

Понятие достоверного и невозможного события используется для

количественной оценки возможности появления того или иного явления, а с

количественной оценкой связана вероятность.

• Вероятность — численная мера возможности наступления некоторого события.

• Вероятностное пространство

• Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.

Вероятностное пространство.

Вероя́тностноепростра́нство — понятие, введённое А. Н. Колмогоровым в 30-х годах XX века для формализации понятия вероятности, которое дало начало бурному развитию теории вероятностей как строгой математической дисциплины.

Вероятностное пространство — это тройка 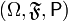(иногда обрамляемая угловыми скобками: 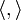), где

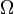§ — это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;

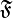§ — сигма-алгебра подмножеств 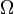, называемых (случайными) событиями;

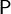§ — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что .

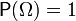Замечания

§ Элементарные события (элементы 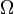), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один.

§ Каждое случайное событие (элемент 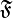) — это подмножество 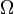. Говорят, что в результате эксперимента произошло случайное событие 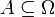, если (элементарный) исход эксперимента является элементом .
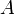Требование, что 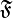является сигма-алгеброй подмножеств 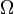, позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности дополнения любого события.

Простым и часто используемым примером вероятностного пространства является конечное пространство. Пусть 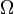— конечное множество, содержащее 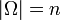элементов.

В качестве сигма-алгебры удобно взять семейство подмножеств 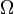. Его часто символически обозначают 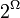. Легко показать, что общее число членов этого семейства, т.е. число различных случайных событий, как раз равно 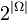, что объясняет обозначение.

Вероятность, вообще говоря, можно определять произвольно. Часто, однако, нет причин считать, что один элементарный исход чем-либо предпочтительнее другого. Тогда естественным способом ввести вероятность является:

,

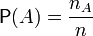где 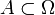, и 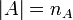- число элементарных исходов, принадлежащих .

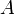В частности, вероятность любого элементарного события: