Многоканальная СМО с ожиданием и ограничением на длину очереди

Пусть СМО имеет не один канал, а несколько (n≥1)^[7], на который поступает пуассоновский поток заявок П_вх с интенсивностью 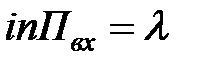. Поток обслуживания простейший и имеет интенсивность m. Заявка, поступившая на вход в момент, когда все каналы занят обслуживанием не покидает систему, а становится в очередь и ожидает обслуживания. Далее предполагаем, что в данной системе имеется ограничение на длину очереди, под которой понимается максимальное число мест в очереди, а именно то, что в очереди могут находиться максимум m заявок (m≥1). Поэтому заявка, пришедшая на вход СМО, в момент, когда в очереди уже стоят m заявок, получает отказ и покидает систему необслуженной.

Итак, рассматриваемая СМО относится к системам смешанного типа с ограничением на длину очереди.

Таблица 8.11 - Параметры многоканальной СМО с ожиданием и ограничением на длину очереди

№ п/п	Параметры	Обозначения, значения, формулы
1.	Число каналов обслуживания	n≥1
2.	Максимальная длина очереди (максимальное число мест в очереди)	m≥1
3.	Интенсивность входящего простейшего потока заявок Пвх	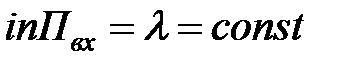, (l не зависит от времени t)
4.	Производительность канала – интенсивность простейшего «потока обслуживаний» Поб (среднее число заявок, обслуживаемое каналом за единицу времени при непрерывной работе канала без простоя)	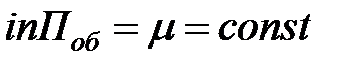, (m не зависит от времени t)

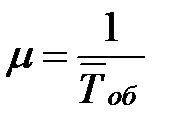Таблица 8.12 - Предельные характеристики эффективности функционирования многоканальной СМО с ожиданием и ограничением на длину очереди

№ п/п	Предельные характеристики	Обозначения, формулы
1.	Показатель нагрузки СМО - трафик системы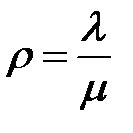
2.	Показатель (коэффициент) нагрузки, приходящейся на один канал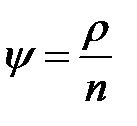
3.	Вероятности того, что все каналы свободны (вероятность простаивания всей системы)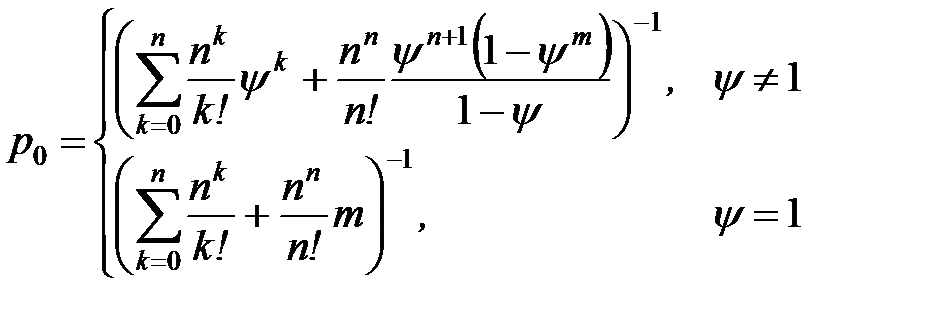
4.	Вероятности состояний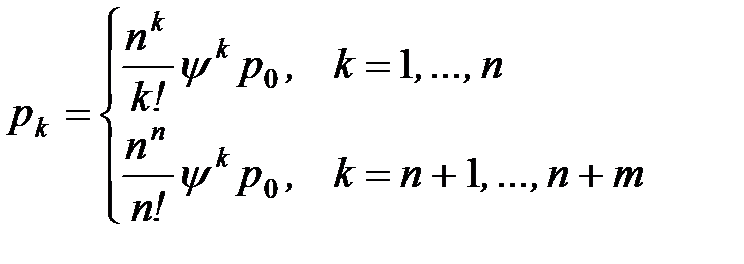
5.	Вероятность отказа заявке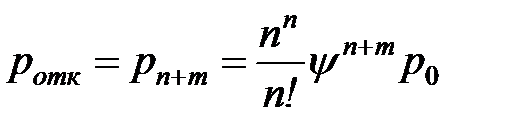
6.	Вероятность того, что заявка будет принята в СМО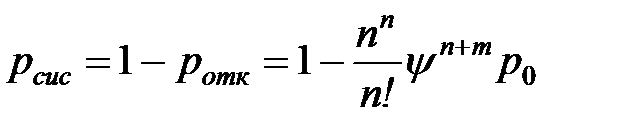
7.	Относительная пропускная способность СМО (средняя доля обслуженных заявок среди поступивших)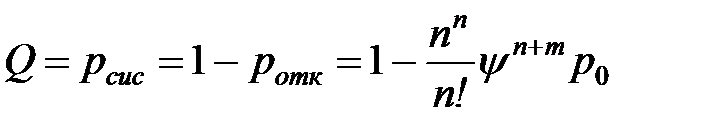
8.	Абсолютная пропускная способность СМО (среднее число обслуживаемых заявок за единицу времени)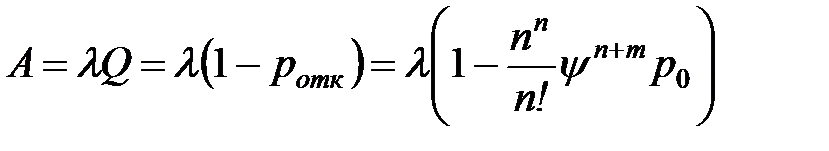
9.	Среднее число занятых каналов (т.е. среднее число заявок, находящихся под обслуживанием)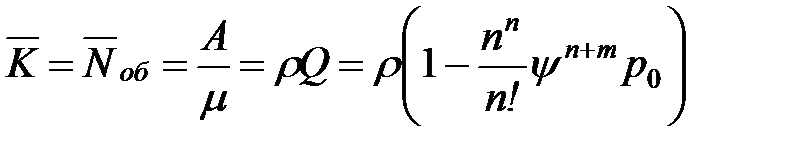

Продолжение таблицы 8.12

№ п/п	Предельные характеристики	Обозначения, формулы
10.	Среднее число заявок, находящихся в очереди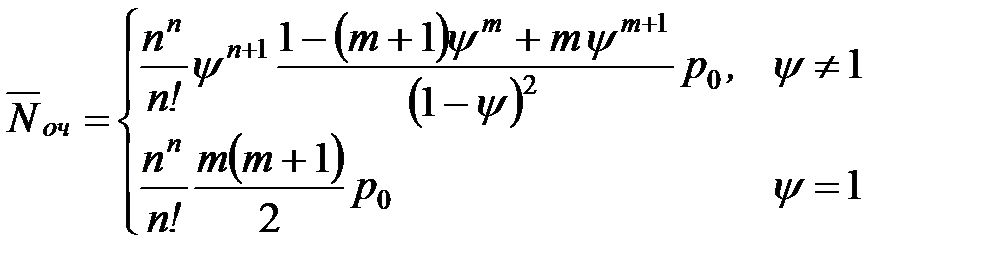
11.	Среднее число заявок, находящихся в системе (как в очереди, так и под обслуживанием)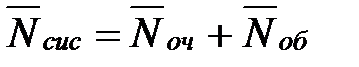
12.	Среднее время ожидания заявки в очереди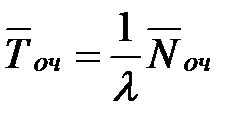
13.	Среднее время пребывания заявки в СМО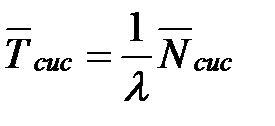
14.	Среднее время обслуживания одной заявки, относящееся ко всем заявкам, как к обслуженным, так и получившим отказ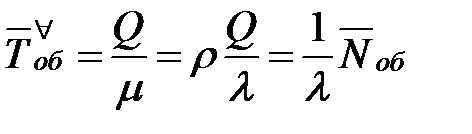

Задача 8.5

На АЗС имеется четыре колонки. Площадка при станции, на которой машины ожидают заправку, вмещает не более трёх машин одновременно и, если она занята, то очередная машина, прибывшая к станции, в очередь не становится, а уезжает дальше. Машины прибывают на станцию с интенсивностью 0,6 машина в минуту. Интенсивность процесса обслуживания 0,4 машины в минуту. Определить:

· Вероятность того, что все колонки свободны;

· Вероятность отказа в обслуживании;

· Относительную и абсолютную пропускные способности СМО;

· Среднее число машин, находящихся на обслуживании;

· Среднее число машин, ожидающих заправки;

· Среднее число машин на станции;

· Среднее время ожидания машины в очереди;

· Среднее время пребывания машины на АЗС;

· Среднее время обслуживания одной машины, относящееся ко всем машинам, как к обслуженным, так и получившим отказ.

Решение:

В условиях задачи математической моделью АЗС является многоканальная СМО с ожиданием и ограничением на длину очереди, имеющая своими параметрами:

число каналов обслуживания n=4; ограничение на длину очереди m=3;

интенсивность входящего потока 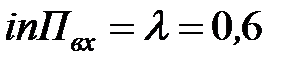(маш./мин);

интенсивность потока обслуживаний 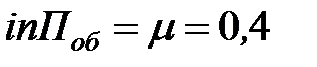(маш./мин);

показатель нагрузки СМО 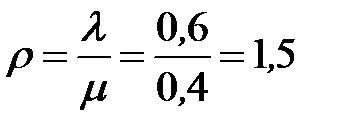(эрланга);

показатель нагрузки, приходящийся на один канал .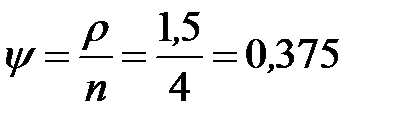

Определим вероятность того, что все каналы свободны (вероятность простаивания всей системы):

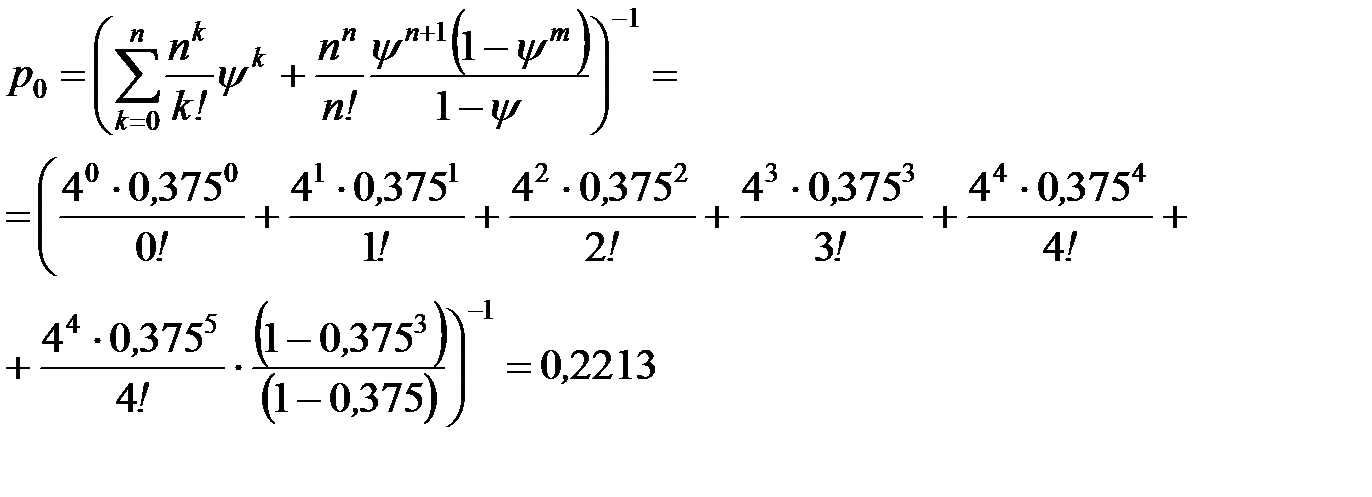
- то есть в вероятность того, что все колонки свободны равна 0,2213.

Находим вероятность отказа в обслуживании:

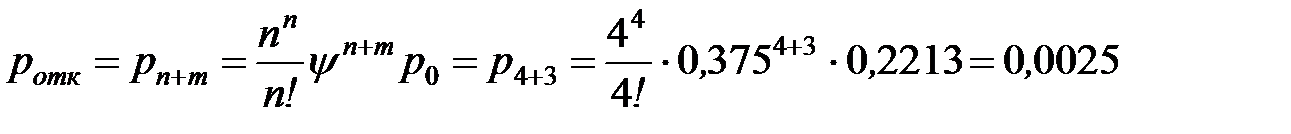
- то есть в вероятность отказа в обслуживании (когда заправляются 4 машины и в очереди 3 машины) равна 0,0025.

Определим значение относительной пропускной способности:

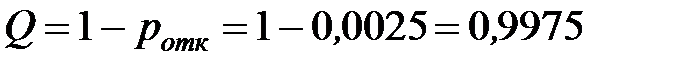или 99,75% - то есть в установившемся режиме из 100 машин практически все будут обслужены.

Определим значение абсолютной пропускной способности:

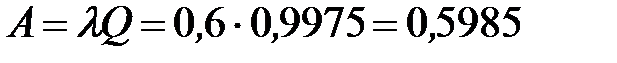- то есть в установившемся режиме абсолютная пропускная способность 0,5985 машин в минуту.

Определим среднее число заявок, находящихся под обслуживанием:

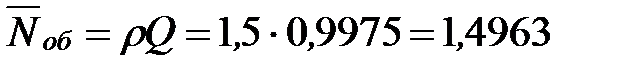- то есть в установившемся режиме среднее число машин, находящихся под обслуживанием равно одной машине.

Определим среднее число заявок в очереди:

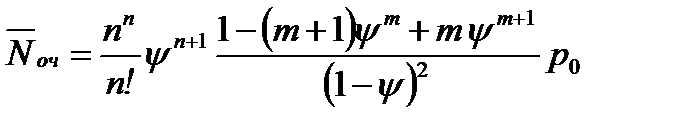
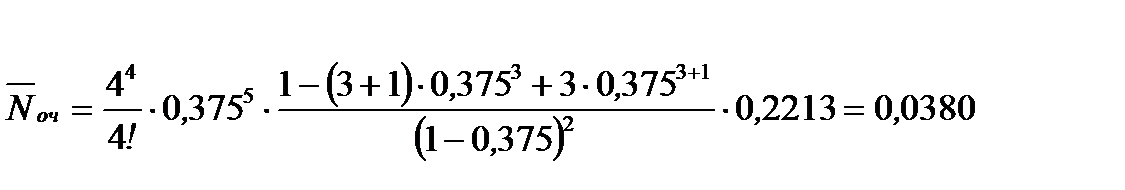
- то есть в установившемся режиме среднее число машин, ожидающих заправки равно 0.

Определим среднее число заявок, находящихся в системе:

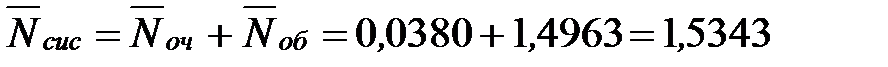- то есть в установившемся режиме среднее число машин, связанных с АЗС равно двум машинам.

Определим среднее время ожидания заявки в очереди:

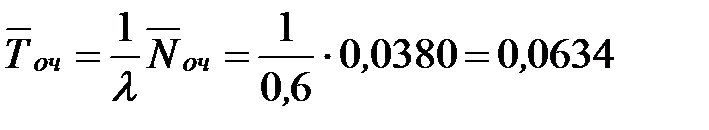- то есть в установившемся режиме среднее время ожидания машины в очереди составляет 0,1 минуты.

Определим среднее время пребывания заявки в СМО:

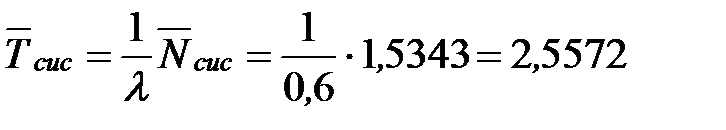- то есть в установившемся режиме среднее время, проведённое машиной на станции, составляет 2,6 минуты.

Определим среднее время обслуживания одной заявки, относящееся ко всем заявкам, как к обслуженным, так и получившим отказ:

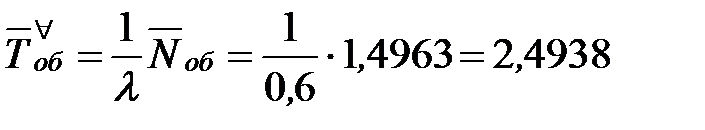- то есть в установившемся режиме среднее время обслуживания одной машины относящееся ко всем машинам – и обслуженным, и необслуженным, составляет 2,5 минуты.

Контрольные вопросы

1. Чему равно число состояний системы для n-канальной СМО с ограничением на длину очереди в m заявок?

2. Когда существуют предельные вероятности состояний для одноканальной для n-канальной СМО с ограничением на длину очереди в m заявок?

3. Чему равна вероятность отказа для n-канальной СМО с ограничением на длину очереди в m заявок?

4. Чему равна вероятность того, что очереди нет для n-канальной СМО с ограничением на длину очереди в m заявок?

5. Чему равна вероятность нахождения в очереди r заявок для n-канальной СМО с ограничением на длину очереди в m заявок?

6. Какие номера принимает время ожидания в очереди для n-канальной СМО с ограничением на длину очереди в m заявок?

7. Чему равна абсолютная пропускная способность для n-канальной СМО с ограничением на длину очереди в m заявок?