Квадратные корни. Квадратные уравнения. Неравенства

Эти темы — особенные для 8 класса. Расширение понятий

о числе и функциях.

Формирование навыка решения квадратных уравнений, чис-ловых и линейных неравенств. Чтобы достичь опорного уровня, необходимо больше времени уделять повторению, обобщению

и систематизации учебного материала, чтобы ученик с невысоким уровнем математической подготовки адаптировался к изучению нового материала на следующей ступени обучения.

Изучение алгебры в 9 классе Квадратичная функция

Курс алгебры в 9 классе начинается с темы «Квадратичная функция», на изучение которой отводится 28 часов. Вводное по-вторение отдельно не планируется, а включается в уроки изучения нового материала.

На первых уроках актуализируется понятие «функция» с по-

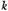
мощью примеров изученных ранее функций: y = kx + b, 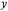y = x2,

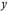
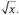y = x3, Обобщая изученный материал на конкретных при-мерах, иллюстрированных графиками приведенных функций, формулируются общие свойства функций, такие как область определения функции, область значений функций, возрастание

и убывание, нули функции, промежутки знакопостоянства функ-ции. Затем эти свойства анализируются для любых функций. Со-ставляется алгоритм исследования функций. Опорой для работы по этой теме служат готовые графики функций.

Сложность выполнения заданий учащимися состоит в том, что у большинства учащихся вследствие основного заболевания

нарушены пространственные представления и координация движе-ний, что отражается на работе с прямоугольной системой координат. Снять напряжение при этом помогают крупный рисунок, готовый единичный отрезок, частично выполненное построение. Способ-ствовать формированию навыков чтения графиков функции помога-ют карточки с рисунками, тетради с печатной основой или отдельно напечатанные задания с рисунком, плакаты, использование компью-терных технологий для проведения тестов и контрольных работ.

Изучение тем « Квадратный трехчлен » и «Разложение ква-дратного трехчлена на множители» (5 ч) подготовит учащихся

к дальнейшему изучению свойств квадратичной функции. На дан-ном этапе повторяются тема «Решение квадратных уравнений», формулы дискриминанта и корней квадратного уравнения. Для работы с формулами полезно видеть их постоянно перед собой, так как учащиеся коррекционной школы имеют кратковременную память. Формулы дискриминанта D = b2 – 4a и корней квадрат-

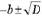
ного уравнения 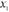вывешиваются на дополнительную

доску «К уроку» или раздается справочный материал, накоплен-ный за годы учебы. Работа в классе по этой теме часто происхо-дит фронтально, проговариваются разные способы нахождения корней квадратного уравнения, включая использование прямой

и обратной теорем Виета для нахождения корней или проверки полученных корней; комментируются и вычисления. Некоторые сложности возникали с воспроизведением способов решения не-полных квадратных уравнений. Здесь следует обратить внимание на нерациональность применения формул в легких случаях. От-работка этих затруднений носит индивидуальный характер.

Новая формула разложения квадратного трехчлена на мно-

жители ax2 + bx + c = a(x – x₁)(x – x₂) закрепляется в самостоятель-

ных упражнениях, на первых этапах часто используется шаблон ax2 + bx + c = a(x – ...)(x – ...),для заполнения которого необходимотолько вычисление корней квадратного трехчлена.

Изучение функции y = ax2 + bx + c проводится по составленному ранее алгоритму.

Построение графиков квадратичной функции: y = ax2, y = ax2 + n, y = a(x – m)2, y = a(x – m)2 + n в основном проводим с помощью ша-

блонов (шаблонной линейки) y = x2, y = 2x2, 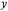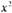посредством па-

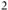
раллельных переносов вдоль осей Ох или Оу.

Обобщая изученный материал, подводим учащихся к алгоритму построения графика квадратичной функции y = ax2 + bx +c. При этом следует уделять внимание формированию умения указывать коор-динаты вершины параболы, ее ось симметрии, направление ветвей параболы. При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак.

Ведущей целью при изучении этого учебного материала ста-вится умение описать этапы построения, схематичного изобра-жения от руки графика квадратичной функции, принимая во вни-мание значительные двигательные нарушения у детей вследствие ДЦП. А следовательно, ответы на вопросы о преобразовании гра-фиков функций вообще носят описательный характер. Возмож-ность использования ИКТ на уроках алгебры существенно облег-чает работу по данной теме.

Основная цель —выработать представление о построении графи-ка квадратичной функции и применять графические представления для решения неравенств второй степени с одной переменной.

При изучении темы «Степенная функция» (3 ч) основной це-лью является введение понятия корня n-й степени. В данной теме продолжается изучение свойств функции: выводятся понятия чет-ной и нечетной функции, рассматриваются (повторяются) свойства степенной функции с натуральным показателем. Изучение корней ограничивается введением понятия корня n-й степени и выполне-ния заданий на вычисление корней n-й степени, в частности, ку-бических корней. Свойства корней n-й степени, понятие степени

с рациональным показателем и ее свойства не изучаются. Этот ма-териал будет рассмотрен в старшей школе.

Уравнения и неравенства

Основная цель —выработать умение решать простейшие систе-мы, содержащие уравнения второй степени с двумя переменными,

и решать текстовые задачи с помощью составления таких систем.

В этой теме завершается изучение рациональных уравнений с одной переменной. В связи с этим проводится некоторое обобще-ние и углубление сведений об уравнениях. Даются понятия цело-го рационального уравнения и его степени. Учащиеся знакомятся с решением уравнений третьей и четвертой степени с помощью раз-ложения на множители и введения вспомогательной переменной.

170 171

Метод решения уравнений путем введения вспомогательной пере-менной будет широко использоваться в дальнейшем при решении тригонометрических, логарифмических и других видов уравнений.

В данной теме завершается изучение уравнений с двумя перемен-ными и их систем. Вводится уравнение окружности (x – a)2 + (y – b)2 = r2. Рассматриваются системы, содержащие уравнения второй степени

с двумя переменными. Основное внимание уделяется системам, в которых одно уравнение первой степени, а другое — второй. Из-вестный учащимся способ подстановки находит здесь дальнейшее

применение и позволяет сводить решения таких систем к реше-

нию квадратного уравнения. Решение систем уравнений с двумя переменными, в которых оба уравнения второй степени, не явля-ется обязательным и может быть рассмотрено только на неслож-ных примерах.

С помощью графических представлений можно наглядно по-казать учащимся, что система двух уравнений с двумя переменны-ми второй степени может иметь одно, два, три, четыре решения, а может и вовсе не иметь решений.

Важно обратить внимание учащихся на то, что математиче-ский аппарат, охваченный данной темой, позволяет существен-но расширить класс содержательных текстовых задач, решаемых

с помощью систем уравнений.

Основные трудности при изучении этой темы связаны с боль-шим объемом записей, что остается значительной преградой для детей с последствиями заболевания ДЦП. Чтобы не потерять цель, поставленную на уроке, по нашему опыту рекомендуется суще-ственно сокращать объем письменных работ. Переносить выполне-ние части задания в устную работу, обсуждая план решения (алго-ритм), используемые формулы, правила и свойства при решении алгебраических уравнений и неравенств. Для экономии времени на уроке задания даются в виде шаблонов, где часть письменной работы выполнена, — например, напечатано условие, начало ре-шения, которое следует закончить. Используются приемы анали-за приведенного текста решения — «найди ошибку». При решении дробно-рациональных уравнений, связанных с большим объемом преобразований, особо обращаем внимание на проверку получен-ных корней уравнения. При решении систем уравнений обсужда-ем приемы решения, при этом акцентируем внимание на выборе наиболее рационального способа.

Не секрет, что вычислительные навыки у большинства учащих-ся находятся на весьма низком уровне, что сводит на нет всю само-стоятельную работу по решению уравнений и их систем. Здесь необ-ходимы постоянный контроль и помощь учителя, систематическое обучение самоконтролю и рефлексии при выполнении заданий. Про-ведение на уроках небольших самостоятельных работ (1–2 задания)

с обязательной проверкой в классе с помощью готовых ответов или полных верных решений способствует формированию рефлективных навыков по нахождению места и причины ошибок.

Формирование умений решать неравенства вида ax2 + bx + c > 0, ax2 + bx + c < 0,где a ≠ 0,осуществляется с опорой на сведения о гра-фике квадратичной функции (направление ветвей параболы, ее расположение относительно оси ОХ).

Прогрессии

Основная цель —дать понятия об арифметической и геометриче-ской прогрессиях как числовых последовательностях особого вида.

В начале изучения темы разъясняется смысл понятий «после-довательность», «n-ый член последовательности», вырабатыва-ется умение использовать индексные обозначения. Эти сведения используются при введении понятий арифметической и геоме-трической прогрессий, выводе формул n-го члена и суммы n пер-вых членов для каждой из прогрессий. При изучении темы можно ограничиться только одной формулой для нахождения суммы n первых членов арифметической прогрессии, а именно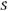

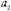
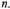
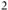
(см. Приложение 1)

Для геометрической прогрессии достаточно рассмотреть одну

формулу суммы n первых членов прогрессии .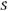

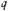
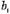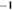
При выполнении упражнений основное внимание уделяется за-даниям, связанным с непосредственным применением изучаемых формул, а также задачам практического содержания. Сведения

о бесконечно убывающей геометрической прогрессии не являются обязательными. Сложность данных тем — в большом количестве используемых формул. Имея в виду нарушенные функции мыш-ления у большинства учащихся, для выбора нужной формулы ре-комендуется открыто использовать справочные материалы всеми доступными способами.

Элементы комбинаторики и теории вероятностейРекомендуем рассмотреть обзорно на интересных задачах, ил-

люстрируя математический аппарат в особых разделах математи-ки: теории информации, линейном программировании.

Итоговое повторение

Основная цель —обобщение и систематизация полученных зна-ний в течение года, корректировка пробелов и ошибок. Подготовка к следующему этапу обучения.

На уроках итогового повторения возможно проведение не-стандартных уроков, презентаций, проектных работ, где в нетра-диционной форме происходит обобщение и закрепление учебных знаний, умений и навыков, установление межпредметных связей и устойчивого интереса к математике.

Приложение

Урок алгебры в 9а классе

Учитель высшей категории Толстикова Ольга Алексеевна Информационная карта урока № 3/4 Модуль № 3 «Арифметическая прогрессия»

Тема: «Формулаn-го члена арифметической прогрессии»

Тип урока: комбинированный

Микроцели урока

Для ученика	Для учителя
1. Учиться находить место затрудне-	Коррекционные:
ния и ошибки в домашнем задании	– тренировать способность рабо-
2. Знать определение арифметиче-	тать по алгоритму (по формулам);
ской прогрессии и способ нахожде-	– развивать и корректировать мысли-
ния членов арифметической про-	тельные процессы: память, внимание,
грессии по формуле	анализ, синтез, сравнение, логику;
	– развивать речь учащихся;
3. Уметь работать с формулой n-го
члена арифметической прогрессии	– развивать способность к самосто-
при решении задач на нахождение	ятельной работе;
– развивать рефлексивные способ-
недостающих членов прогрессии; раз-
ности прогрессии и ее первого члена	ности учащихся

Для ученика	Для учителя
4. Тренировать способность рабо-	Образовательные:
тать самостоятельно	– проверить сформированность по-
5. Учиться проводить рефлексию	нятия арифметической прогрессии
	и характеристического свойства ее
	членов;
	– формировать умение работать
	с формулой n-го члена арифмети-
	ческой прогрессии, решая задачи
	на нахождение недостающих чле-
	нов арифметической прогрессии,
	разности прогрессии, первого чле-
	на прогрессии;
	– проверить уровень сформирован-
	ности знаний и навыков по теме
	Воспитательные:
	– прививать аккуратность при веде-
	нии записей в тетрадях;
	– развивать коммуникативные спо-
	собности;
	– развивать интерес к математике
	для успешной учебы
Опорные понятия, термины	Новые понятия, термины
Арифметическая прогрессия, раз-
ность (d) арифметической прогрес-
сии, формула n-го члена арифмети-
ческой прогрессии, характеристи-
ческое свойство членов арифмети-
ческой прогрессии

174 175

Этапы урока, форма,				Обратная связь
Методический инструментарий	(Деятельность
краткое содержание
			обучающихся)
1. Самоопределение	Задание, в котором возникли затруднения, — на доске	1. Устные ответы уча-
обучающихся				щихся, рефлексия до-
(Вопросы: какую тему изуча-				машней работы; на-
ем? Что уже умеем делать по	Формулы арифметической прогрессиина доске	строй на учебную де-
этой теме? Какие формулы вы	ятельность
использовали во время выпол-
нения домашней работы? Где	d = an+1 – an
вы испытывали затруднения?)
Проверка домашней	an = a1 d(n – 1)
работы.
Устная работа с опорой
на формулы
2. Актуализация знаний и навы-	Задания на доске:	2. Фронтальная
ков учащихся, необходимых для	1. Какие последовательности являются арифметиче-	работа
работы на уроке	скими прогрессиями?
	а) 3; 7; 11; 15; …
	б) 1; 2; 3; 4; 5; …
	в) –4; –2; 0; 4; 8; …
	г) 0; –1; 1; –2; 2; …
	Сформулировать определение арифметической прогрессии.

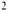
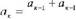
	Этапы урока, форма,		Обратная связь
	Методический инструментарий	(Деятельность
	краткое содержание
		обучающихся)
		2. Найти неизвестные члены прогрессии:
		÷ (án) : a1; a2; – 19; – 12; a5; ...
		Как найти предыдущий член арифметической прогрессии?
		Как найти последующий член арифметической прогрессии?
		3. План к решению задачи № 349, аналогичной в домаш-
		нем задании:
		а) Значения пути, пройденного телом в каждую следу-
		ющую секунду, составляют арифметическую прогрес-
		сию с разностью… (d = ?);
		б) Найдем а8:
		а8 = a1 + d(8 – 1) = ...
	3. Обобщение знаний об ариф-	Задание на доске:	3. Подводящий диалог.
	метической прогрессии	Дано: арифметическая прогрессия	Устные ответы
			учащихся
		(án) : –21; – 18; ...
	4. Тренировочные упражнения	Найти, под каким номером в эту прогрессию входит	4. Письменная рабо-
		число 0?	та с комментариями
		Задача № 349 (учебник, с. 87)

					Продолжение таблицы
Этапы урока, форма,					Обратная связь
	Методический инструментарий	(Деятельность
краткое содержание
				обучающихся)
	Индивидуальное задание:
	Используя формулу		, найдите неизвестные
	члены арифметической прогрессии:
		4; _; 8; _; 12; 14; 16;...
5. Самостоятельная работа		Задания по уровням на листках:	5. Самостоятельное
	Самостоятельная работа		выполнение задания
	Уровень I		на листках
	1. В арифметической прогрессии (an) известны a1 = 3,
	d = 4. Найти a11.
	2. Найти разность арифметической прогрессии (yn),
	если y1 = 12, y5 = 18.
	Решение.
	y	= 18;
	y55	= y1+ d(4–1)
	Подставим известные значения для y5 и y1 и получим
	уравнение ……………..........
	Решим уравнение и найдем разность d.
	ОТВЕТ:

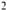
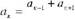
Этапы урока, форма,			Обратная связь
	Методический инструментарий	(Деятельность
краткое содержание
		обучающихся)
	3. В арифметической прогрессии (xn) x1 = 3 и d = 2.
	Найти номер члена прогрессии, равного 49.
	Решение.
	В формулу n-го члена хn=x1+ d (n-1)
	подставим значения x1 = 3 и d = 2.
	Получим уравнение: …………………………
	Решим его и найдем значение n.
	ОТВЕТ:
	Самостоятельная работа
	Уровень II
	1. В арифметической прогрессии (bn) известны b1 = 3,
	d = 4. Найти b7 и b11.
	2. Найти разность арифметической прогрессии (аn),
	если a1 = 5, a8 = –1,3.
	Решение:
	a	= –2,3;
	a88	= а1+ d(8–1).
	Подставим известные значения для а8 и а1 и получим
	уравнение……………..........
	Решим уравнение и найдем разность d.
	ОТВЕТ:

Продолжение таблицы	Обратная связь(Деятельность	обучающихся)			6. Рефлексия выпол-	нения самостоятель-нойработы(устно).Оценкасобственнойдеятельности	7. Возможные вопро-	сы по домашнему за-	данию
	Методическийинструментарий		3.Варифметическойпрогрессии(x	Найтиномерчленапрогрессии,равного	Готовыеответыкзаданиямпоуровнямнакарточках	(илинадоске)—длявизуальногоконтроля	1)учебник:§7,п.16,с.88,№350;	2)заданиевтетради:найтисумму100первыхнату-	ральныхчисел
			= 11 и d = 0,5.	34.
			) x
			n
	Этапы урока, форма,краткоесодержание			6. Подведение итогов урока		7. Домашнее задание с коммен-	тированием

Урок алгебры в 9а классе

Учитель высшей категории Толстикова Ольга Алексеевна

Информационная карта урока № 3/8

Модуль № 3 «Арифметическая прогрессия»

Тема: «Формула суммы n первых членов арифметической про-грессии»

Для ученика	Для учителя
1. Учиться находить место за-	Коррекционные:
труднения и ошибки в домаш-	– тренировать способность работать
нем задании	по алгоритму (по формулам);
2. Познакомиться с выводом	– развивать и корректировать мысли-
формулы суммы n первых чле-	тельные процессы: память, внимание,
нов арифметической прогрессии	анализ, синтез, сравнение, логику;
	– развивать речь учащихся;
3. Научиться работать с фор-
мулой суммы n первых членов	– развивать рефлексивные способно-
арифметической прогрессии при	сти учащихся
решении задач
	Образовательные:
	– актуализировать знания формул ариф-
	метической прогрессии;
	– вывести новую формулу суммы n пер-
	вых членов арифметической прогрессии;
	– формировать умение работать с фор-
	мулой суммы
	Воспитательные:
	– прививать аккуратность при ведении
	записей в тетрадях;
	– прививать уважительное отношение
	к учебному труду; умение выражать
	и обосновывать свое мнение;
	– развивать интерес к математике, рас-
	ширять научное мировоззрение
Опорные понятия, термины	Новые понятия, термины
Арифметическая прогрессия,	Формула суммыnпервых членов
разность (d) арифметической	арифметической прогрессии
прогрессии, формула n-го члена
арифметической прогрессии

Домашнее задание: Учебник: § 7, п. 17, с. 89–91, №№3 70б)

371 а) или 373.

180 181

	Этапы урока	Методический инструментарий	Обратная связь
	1. Самоопределение учащихся.	Презентация, слайд 3–4 (или задание на доске)	1. Устные ответы
	Проверка домашней работы		учащихся
		Задача № 350
		Поезд, отойдя от станции, равномерно увеличивал скорость
		на 50 м в минуту. Какова была скорость поезда в конце двад-
		цатой минуты?
		Решение:
		Последовательность чисел: 50; 100; 150; … является арифме-
		тической прогрессией.
		Поэтому можно считать, что:
		Дано:(аn) — арифметическая прогрессия,
		а1 = 50; d = 50. Найти: а20 =?
		Решение.
		По формуле n-го члена найдем а20:
		а20 = а1 + d(20 – 1) = 50 + 50 × 19 = 1000.
		Значит скорость поезда в конце 20-й минуты равна 1000 м/мин.
		1000 м/мин = 1000 × 60 : 000 км/ч = 60 км/ч
		Ответ: 60 км/ч.
	2. Актуализация знаний и на-	Презентация, слайд 5–6 (или задание на доске)	2. Фронтальная
	выков учащихся, необходимых		работа
	для новой темы	Задание 2
		Является ли последовательность 1; 2; 3; 4; …; 100.
		арифметической прогрессией?

	Этапы урока	Методический инструментарий	Обратная связь
	3. Вывод новой формулы суммы	...........................................	3. Подводящий
	n первых членов арифмети-	Из домашнего задания:	диалог
	ческой прогрессии на основе	Найдите сумму натуральных чисел от 1 до 100.	Запись темы на до-
	домашней задачи.
		1 + 2 + 3 + 4 + … + 100 = ?	ске и в тетрадях
		Ответ: 5050.	Визуальное и вер-
	Исторические сведения	Иоганн Карл Фри́дрих Га́усс (нем. Johann Carl Friedrich Gauß);
	по теме	1777–1855 — немецкий математик, астроном и физик, счи-	бальное закрепле-
		тается одним из величайших математиков всех времен, «ко-	ние нового мате-
		ролем математиков».	риала
	Знакомство с решением Гаус-	«Формула суммы n первых членов
	сом задачи. Формулировка	арифметической прогрессии»
	темы урока
	Доказательство новой формулы	Презентация, слайд 10
		Формула суммы n первых членов арифметической про-
		грессиина доске.
	4. Тренировочные упражнения	Примеры на доске, презентация, слайд 11–12	4. Устные ответы
		Задача 1	учащихся