Задачи нечеткой классификации

Пусть имеется набор фотографических портретов всех членов нескольких семей. Требуется разделить этот набор на группы так, чтобы в каждой оказались портреты членов только одной семьи. Пусть — функция принадлежности нечеткого бинарного отношения сходства на заданном наборе фотографий. Для каждой пары фотографий и значение есть субъективная оценка человеком степени сходства и . Это нечеткое отношение можно рассматривать как своего рода "экспериментальные данные", отражающие понимание человеком понятия "сходства" в данной задаче. Следующий этап — использование этих "данных" для требующейся классификации фотографий.

Заметим, что нечеткое отношение обладает естественными свойствами рефлексивности и симметричности. Оно называется одношаговым отношением, в том смысле, что описывает результаты лишь попарного сравнения портретов друг с другом. Для вводится 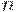-шаговое отношение следующим образом:

Это отношение является 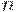-арной композицией исходного "экспериментального" отношения и представляет собой в некотором смысле его уточнение. Нетрудно показать, что для любых выполняется цепочка неравенств

из которой следует, в частности, что для любых последовательность имеет предел при . Таким образом, существует предельное отношение сходства, определяемое равенством

Это предельное отношение является конечным результатом обработки результатов нечетких измерений и следующим образом используется для классификации.

Для произвольного числа 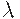( ) вводится обычное (не нечеткое) отношение :

Нетрудно показать, что для любого 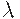( ) есть отношение эквивалентности в , т.е. для любых выполняются обычные аксиомы эквивалентности

(1) — рефлексивность,

(2) — симметричность,

(3) — транзитивность.

Заметим, что (3) есть следствие того, что предельное нечеткое отношение обладает свойством нечеткой транзитивности

Окончательный этап алгоритма классификации — разбиение множества на классы эквивалентности по полученному отношению .

Выбор величины порога 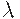в этом алгоритме осуществляется, исходя из условий начальной задачи. В приведенном выше примере с фотографиями этот выбор осуществляли следующим образом. Пусть имеется набор из 20 фотографий представителей 3 семей. Тогда величину 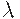выбирают так, чтобы в результате реализации алгоритма классификации получилось 3 класса эквивалентности по отношению .

Порядки и слабые порядки

Антисимметричное, транзитивное нечеткое отношение 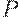называется отношением упорядочения или порядком. Мы будем рассматривать только строгие порядки, т.е. порядки, для которых выполняется свойство антирефлексивности. Свойства нестрогих (рефлексивных)порядков во многом совпадают со свойствами строгих порядков.

Различные порядки отличаются друг от друга требованиями, предъявляемыми к условию транзитивности. Слабейшее из этих требований — условие ацикличности отношения строгого порядка 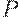, наиболее жесткие требования — условия линейной транзитивности и условие квазисерийности.

Если для отношения сходства условие транзитивности обычно записывают в виде и различные способы определения операции композиции позволяют задавать разные типы транзитивности, причем оказывается, что таких типов существует не так уж и много, то для отношения порядка условие транзитивности нечеткого отношения удобно записывать в виде, аналогичном условию транзитивности обычных порядков:

где — некоторая операция в . Оказывается, что из множества всех отношений порядка можно выделить значительное количество отличающихся друг от друга классов порядков специального вида, определяемых как способом задания операции в , так и способом записи условия транзитивности. Далее перечислим некоторые условия транзитивности, определяющие эти классы нечетких строгих порядков. Учитывая асимметричность отношения строгого порядка 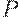, будем полагать , если .

Ацикличность:

Слабая транзитивность:

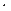Отрицательная транзитивность:

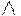( )- транзитивность:

( )- транзитивность:

( )- транзитивность:

Сильная транзитивность:

Сверхсильная транзитивность:

Метрическая транзитивность:

Квазисерийность:

Ультраметрическая транзитивность:

В общем случае предполагается, что рассмотренные условия транзитивности определены для 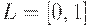, хотя некоторые условия могут быть обобщены и на случай, когда является решеткой.

Условия ацикличности, слабой транзитивности и отрицательной транзитивности нечеткого отношения 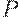равносильны соответственно условиям ацикличности, транзитивности и отрицательной транзитивности обычного отношения , определяемого следующим образом:

Аналогичные свойства могут быть определены как 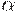-свойства для различных 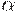-уровней отношения .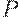

В отличие от первых трех свойств, остальные свойства более специфичны для нечетких отношений и в большей мере учитывают согласованность силы отношения между элементами множества . Для этих свойств также могут быть сформулированы 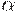-свойства.

Частным случаем сильного порядка (порядка, удовлетворяющего условию сильной транзитивности) является метрический порядок. Для асимметричных отношений условие метрической транзитивности эквивалентно неравенству треугольника.

Условие квазисерийности определяет нечеткую квазисерию. Каждый 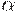-уровень нечеткой квазисерии является обыкновенной квазисерией, т.е. удовлетворяет условиям

Поскольку обычная квазисерия определяет разбиение множества на упорядоченные классы эквивалентности, нечеткая квазисерия определяет разбиение множества на упорядоченные классы эквивалентности на каждом 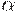-уровне. Эти разбиения вложены друг в друга; таким образом, нечеткая квазисерия определяет иерархию разбиений множества на упорядоченные классы эквивалентности.

Частным случаем метрических порядков, помимо квазисерии, является линейный порядок, определяемый условием линейной транзитивности. Линейный порядок при интерпретации как силы предпочтения альтернативы над альтернативой задает на множестве альтернатив некоторую аддитивную функцию полезности, которая может быть определена на , например, с помощью соотношения .

Ультраметрическая транзитивность построена по аналогии с метрической транзитивностью, однако для антисимметричныхотношений она не эквивалентна ультраметрическому неравенству .

Между строгими порядками (асимметричными отношениями) и слабыми порядками (рефлексивными отношениями) существует тесная связь. Эти порядки могут быть получены друг из друга с помощью ряда преобразований.

Если на задана операция дополнения, т.е. такая унарная операция , что на выполняются тождества

то на множестве нечетких отношений может быть задана операция дополнения следующим образом:

и на множестве нечетких отношений будут выполняться тождества

Если на множестве нечетких отношений задана операция дополнения, то из отношения строгого порядка 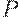могут быть получены:

Отношение сходства

Отношение различия

Отношение слабого порядка

Транзитивностью отношения 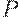определяется тот или иной уровень транзитивности отношени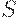й и 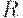. В частности, если 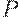является нечеткой квазисерией, то определяемое им отношение 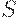является нечетким отношением эквивалентности, аотношение 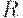будет нечетким квазипорядком.

Нечеткие отношения порядка могут быть получены многими способами и допускают различную интерпретацию. Они могут выражать либо значение какого-либо физического параметра, характеризующего интенсивность доминирования над , либо усредненную по множеству критериев или индивидуумов силу предпочтения между объектами. Они могут быть получены с помощью шкалы сравнений, которой эксперты измеряют интенсивность предпочтений при попарных сравнениях альтернатив, могут выражать уверенность, возможность, вероятность доминирования и т.п.