Теория приближенных вычислений

Основное понятие нечёткой логики в широком смысле — нечёткое множество, определяемое при помощи обобщенного понятия характеристической функции. Затем вводятся понятия объединения, пересечения и дополнения множеств (через характеристическую функцию; задать можно различными способами), понятие нечёткого отношения, а также одно из важнейших понятий — понятие лингвистической переменной.

Вообще говоря, даже такой минимальный набор определений позволяет использовать нечёткую логику в некоторых приложениях, для большинства же необходимо задать ещё и правило вывода (и оператор импликации).

При формализации знаний достаточно часто встречаются качественные знания, например, высокая температура при гриппе, слабое свечение нити накаливания, молодой дипломат и т.д. Для формального представления таких качественных знаний американский математик, профессор информатики в Университете в Беркли (Калифорния) Лофти А.Заде предложил в 1965 году в журнале «Information and Control» формальный аппарат нечеткой (fuzzy) логики.

Лофти А.Заде (Lotfi Askar Zadeh) родился 4 февраля 1921г в Баку,. откуда семья в 1932 году преехала в Иран, где на протяжении 8 лет учился в Американском колледже Тегерана (впоследствии известном как Alborz[en] — миссионерской пресвитерианской школе с персидским языком обучения), затем на электроинженерном факультете в Тегеранском университете (окончил в 1942 году). После окончания университета в июле 1944 года переехал в Соединенные Штаты и в сентябре поступил в Массачусетский технологический институт (получил диплом магистра в области электрической инженерии в 1946 году). Родители Лотфи Заде в это время жили в Нью-Йорке (мать работала врачом), где он поступил в аспирантуру Колумбийского университета, а после защиты диссертации в 1949 году остался там же ассистентом на инженерном отделении. С 1959 года работает в Калифорнийском университете (Беркли).

Лофти Заде рассказывал: «Большая часть знаний, которые мы храним в своём мозгу, неточные. «Джон - старый, а Джейн - молодая». «Майкл живёт около Беркли». «Большинство богатых людей имеют несколько автомобилей». Мы всегда говорим так, но ясно ли из этих фраз, сколько лет Джону и Джейп, каково расстояние от дома Майкла до нашего университета в Беркли, а также, что означают слова «большинство», «несколько», «богатый»? В то же время машины, на которые мы возлагаем сегодня все наши надежды, должны как-то воспринять смысл подобных чисто человеческих высказываний. Вот потому я и пытаюсь разрабатывать свою «размытую логику», которая теперь, мне кажется, превращается уже в теорию приближённых рассуждений, - говорил Лофти Заде и один за другим демонстрировал графики и таблицы, содержавшие ответы на поставленные им в начале доклада вопросы. Вот «кривая молодости». Согласно ей человек молод всю свою жизнь, но только с разным коэффициентом: с единицей в двадцать лет, 0,9 в двадцать пять, 0,8 в тридцать, 0,6 в сорок. Итак, если «Джейн - молодая», то машина знает теперь, что, скажем двадцать восемь лет ей следует считать с вероятностью 0,86. Когда в тексте встречается слово «очень», машина сразу возведёт коэффициент в квадрат, а на сказанное мимоходом «более или менее» отреагирует тем, что извлечёт квадратный корень. Чуть сложнее, но в принципе так же поступит она с «Очень Большим Домом», - здесь, п

Пусть E - универсальное множество, x - элемент E, а R - определенное свойство. Обычное (четкое) подмножество N универсального множества E, элементы которого удовлетворяют свойство R, определяется как множество упорядоченной пары N = {mN (х)/х}, где mN(х) - характеристическая функция, принимающая значение 1, когда x удовлетворяет свойство R, и 0 - в другом случае.

Нечеткое подмножество отличается от обычного тем, что для элементов x из E нет однозначного ответа "нет" относительно свойства R. В связи с этим, нечеткое подмножество N универсального множества E определяется как множество упорядоченных пар N = {μ_N(x)/x}, где μ_N(x) - характеристическая функция принадлежности (или просто функция принадлежности), принимающая значение в некотором упорядоченном множестве M (например, M = [0,1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента x к подмножеству N. Множество M называют множеством принадлежностей. Если M = {0,1}, тогда нечеткое подмножество N может рассматриваться как обычное или четкое множество.

Таким образом, нечеткое множество N можно записать как

nN = Σ(μ(X_i) / X_i), i=1

где X_i - i-е значение базовой шкалы, а знак " Σ" не является обозначением операции сложения, а имеет смысл объединения.

Характеристическая функция

Для пространства рассуждения 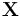и данной функции принадлежности 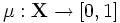нечёткое множество определяется как

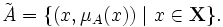
Функция принадлежности 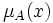количественно градуирует приналежность элементов фундаментальногомножества пространства рассуждения 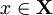нечёткому множеству 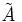. Значение 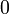означает, что элемент не включен в нечёткое множество, 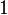описывает полностью включенный элемент. Значения между 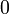и 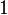характеризуют нечётко включенные элементы.

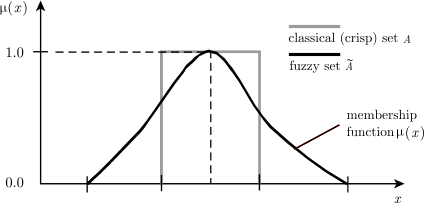
Нечёткое множество и классическое, четкое (crisp) множество