Поверхностные гравитационные волны

Гравитационные волны возникают под действием силы тяжести. Если каким-либо образом поверхность жидкости выведена из состояния равновесия, то сила тяжести, играя роль возвращающей силы, будет стремиться вернуть эту поверхность в ее равновесное положение и заставит каждую частицу колебаться. Движение будет распространяться вдоль всей поверхности в виде волн, называемых гравитационными.

Воспользуемся следующими приближениями: поверхность жидкости будем считать плоской ( =0) и неограниченной, а жидкость несжимаемой и однородной (следовательно, уравнение неразрывности (1.2) будет иметь вид 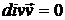). Если амплитуда колебаний в волне много меньше длины волны, то уравнение Эйлера (1.1) можно линеаризовать:

. (7.1)

Очевидно, что в этом случае движение в поверхностной волне является потенциальным и удовлетворяет уравнению Лапласа (4.1) для потенциала скорости ( ):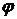

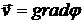. (7.2)

Получим теперь граничные условия, которые должны выполняться на поверхности жидкости и на дне водоема. Пусть давление на свободной поверхности , а возвышение возмущенной поверхности описывается выражением . При этом скорость возвышения поверхности должна совпадать с вертикальной скоростью частиц среды 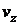, на ней находящихся, поскольку эти частицы не могут ни опережать поверхность, ни отставать от нее.

Из уравнения (7.1) несложно получить линеаризованный вид интеграла Коши (нестационарной формы уравнения Бернулли):

.

Тогда на поверхности жидкости имеем

.

Постоянную можно устранить переопределением потенциала 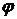, прибавив к последнему независящую от координат величину . Тогда

.

Продифференцируем это соотношение по времени:

.

Считая возмущение поверхности 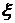малым, можно заменить в граничном условии на поверхности на 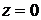, а также линеаризовать выражение для вертикальной компоненты скорости частиц среды: . Поскольку, с другой стороны, , окончательно получаем

. (7.3)

В качестве второго граничного условия возьмем условие «непроникания» (4.2) на неподвижной поверхности дна при :

. (7.4)

Таким образом, гравитационные волны на поверхности жидкости глубиной описываются уравнением (7.2) с граничными условиями (7.3) и (7.4).

Примеры решения задач

1. Получить дисперсионное уравнение для гравитационной поверхностной волны.

Решение: Будем искать решение уравнения (7.2) в виде плоской неоднородной гармонической волны, распространяющейся по оси 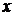, амплитуда которой зависит от :

.

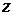Подставив данный вид решения в уравнение Лапласа (7.2), получаем

.

Решением данного уравнения, удовлетворяющим граничному условию на дне

,

является функция , где .

Подстановка последнего выражения в граничное условие при 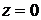показывает, что поверхностная гравитационная волна существует не при произвольных значениях 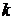и 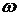, а только при удовлетворяющих дисперсионному соотношению

.

Следовательно, закон дисперсии определяется соотношением между глубиной бассейна и длиной распространяющейся волны .

2. Пусть при возбуждается спектрально-узкий пакет гравитационных поверхностных волн на глубокой воде, содержащий периодов колебаний частотой , модулированный медленно меняющейся функцией времени

,

где при и . Определить:

а) число гребней волны на поверхности, которое увидит неподвижный наблюдатель,

б) сколько колебаний совершит наблюдатель, находящийся в лодке, при прохождении данного волнового пакета.

Решение: Пакет волн распространяется с групповой скоростью, то есть

,

где .

Для стороннего наблюдателя в момент времени 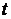пакет будет занимать в пространстве интервал длиной , на котором уложится число волн

.

Поскольку , то

.

Для волн на глубокой воде (см. задачу 7.3) , следовательно,

.

Для наблюдателя, находящегося в лодке в точке 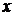, время прохождения пакета равно 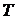, за которое лодка совершит

колебаний.

Задачи для самостоятельного решения

7.1. Показать, что если для поверхностных гравитационных волн выполняется условие ( 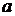- амплитуда волны, - длина волны), то движение жидкости потенциально.

Указание: показать, что в этом случае в уравнении Эйлера можно пренебречь нелинейным членом по сравнению с нестационарным.

a. Получить закон дисперсии волн на глубокой воде. Найти фазовую и групповую скорости волн.

Ответ: , , .

7.2. Показать, что при распространении волны на глубокой воде частицы жидкости в волне двигаются по окружностям с радиусом, экспоненциально убывающим по направлению вглубь жидкости.

7.3. Получить выражение для фазовой и групповой скорости гравитационных волн на мелкой воде ( , где - глубина канала).

Ответ: .

7.4. Сравнить траектории колеблющихся частиц жидкости в потоке конечной глубины у дна и у поверхности жидкости.

7.5. Используя закон дисперсии для гравитационных волн (см. задачу 7.1) на неограниченной поверхности жидкости, глубина которой равна , получить выражение для их групповой скорости.

Ответ: .

7.6. Используя закон дисперсии для гравитационно-капиллярных волн:

,

где ( 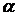- коэффициент поверхностного натяжения), - глубина водоема, получить выражение для их групповой и фазовой скорости. Построить графики , .

7.7. Определить собственные частоты колебаний жидкости в бассейне глубины , длины 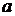и ширины .

Ответ: , где .

7.8. Показать, что для периода 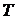океанских волн на глубокой воде справедливо соотношение

,

где - длина океанской волны.

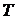7.9. Найти скорость распространения и период колебаний для океанских волн с длиной волны =145 м.

Ответ: = 15м/с, 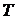=9,6 с.

7.10. Океанские волны перемещаются со скоростью 10 м/с. Найти длину этих волн и их период.

Ответ: = 64 м, 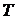= 6,4 с.

7.11. Заметили, что поплавок поднимается и опускается на волне 15 раз в минуту. Найти длину волн и скорость их распространения, считая глубину жидкости очень большой.

Ответ: = 25 м, 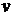= 6,25 м/с.

Контрольные вопросы

1. Поверхностные гравитационные волны.

2. Дисперсионные уравнения для длинных, коротких, гравитационно-капиллярных волн.

3. Фазовые скорости длинных, коротких, гравитационно-капиллярных волн.