Равномерный закон распределения
СВНТ Х называется распределенной равномерно на отрезке [a, b] (при этом для краткости говорят: СВ Х подчиняется закону R(a, b), т.е. Х ~ R(a, b)), если плотность распределения вероятностей постоянна на данном отрезке. Тогда плотность распределения (ПР) f(x) и функция распределения (ФР) F(x) будут иметь следующий вид:
f(x) = 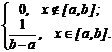 F(x) = F(x) = 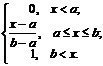 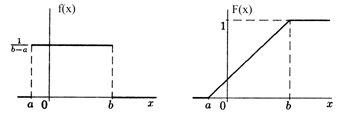 | Основные числовые характеристики СВ Х ~ R(a, b): mX = M[X] = (a + b)/2; nk = M[Xk] = (bk+1 - ak+1)/[(k + 1)×(b - a)], k = 1, 2, ... ; mk = M[(X-mX)k] = [(b - a) k+1 - (a - b) k+1]/[2 k+1×(k + 1)×(b - a)], k = 1, 2, ... ; Mo(X) Î [a, b]; Mе(X) = M[X] = (a + b)/2; t0,5 = Mе(X) = M[X] = (a + b)/2; DX = M[(X - mX)2] = M[X2] - mX2 = (b - a)2/12; sХ = (b - a)/ 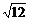 ; A = m3/s3X = 0; E = (m4/s4X) - 3 = -6/5. ; A = m3/s3X = 0; E = (m4/s4X) - 3 = -6/5. |
Это распределение реализуется в опытах, где наудачу ставится точка на отрезке [a, b], а также в экспериментах по измерению тех или иных физических величин с округлением (Х- ошибка округления).
ПОКАЗАТЕЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
СВНТ Х называется распределенной по показательному (экспоненциальному) закону с параметром l > 0 (при этом для краткости говорят: СВ Х подчиняется закону Ех(l), т.е. Х ~ Ех(l)), если ее ПР задается формулой:
f(x) = 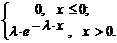
ПР f(x) и ФР F(x) СВ Х ~ Ех(l) имеют следующий вид:
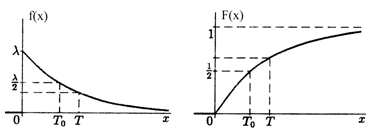
Показательное распределение часто встречается в теории надежности (например, X - срок службы радиоэлектронной аппаратуры).
Задача №1. Пусть Х ~ Ех(l). Построить ФР и ПР. Определить следующие числовые характеристики СВ: mX, mk, Mo(X), Mе(X), DX, sХ, A, E.
НОРМАЛЬНЫЙ (ГАУССОВСКИЙ) ЗАКОН РАСПРЕДЕЛЕНИЯ
СВНТ называется распределенной по нормальному (гауссовскому) закону с параметрами m Î R и s > 0, если ПР задается формулой:
f(x) = 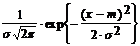 -¥ < x < +¥.
-¥ < x < +¥.
Тогда ПР f(x) и ФР F(x) такой СВ имеют следующий вид:
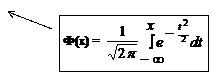
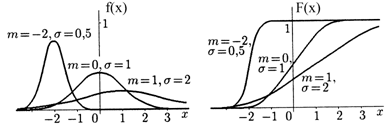
Для краткости говорят, что СВ Х подчиняется закону N(m, s), т.е. Х ~ N(m, s). Параметры m и s совпадают с основными характеристиками распределения: m = mX, s = sХ = 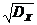 . Если СВ Х ~ N(0, 1), то она называется стандартизованной нормальной величиной. ФР стандартизованной нормальной величиной называется функцией Лапласа и обозначается как Ф(x). С ее помощью можно вычислять интервальные вероятности для нормального распределения N(m, s):
. Если СВ Х ~ N(0, 1), то она называется стандартизованной нормальной величиной. ФР стандартизованной нормальной величиной называется функцией Лапласа и обозначается как Ф(x). С ее помощью можно вычислять интервальные вероятности для нормального распределения N(m, s):
P(x1 £ X < x2) = Ф 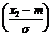 - Ф
- Ф 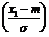 .
.
При решении задач на нормальное распределение часто требуется использовать табличные значения функции Лапласа. Поскольку для функции Лапласа справедливо соотношение Ф(-х) = 1 - Ф(х), то достаточно иметь табличные значения функции Ф(х) только для положительных значений аргумента.
Таблица 1.
Значения функции Лапласа Ф(х) = 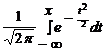
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 | 0,5000 | 0,30 0,31 0,32 0,33 0,34 0,35 0,36 0,37 0,38 0,39 | 0,6179 | 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67 0,68 0,69 | 0,7257 | 0,90 0,91 0,92 0,93 0,94 0,96 0,97 0,98 0,99 | 0,8159 | 1,20 1,21 1,22 1,23 1,24 1,25 1,26 1,27 1,28 1,29 | 0,8849 | 1,50 1,51 1,52 1,53 1,54 1,55 1,56 1,57 1,58 1,59 | 0,9332 |
| 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 | 0,5398 | 0,40 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 | 0,6554 | 0,70 0,71 0,72 0,73 0,74 0,75 0,76 0,77 0,78 0,79 | 0,7580 | 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 | 0,8413 | 1,30 1,31 1,32 1,33 1,34 1,35 1,36 1,37 1,38 1,39 | 0,9032 | 1,60 1,61 1,62 1,63 1,64 1,65 1,66 1,67 1,68 1,69 | 0,9452 |
| 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 | 0,5793 | 0,50 0,51 0,52 0,53 0,54 0,55 0,56 0,57 0,58 0,59 | 0,6915 | 0,80 0,81 0,82 0,83 0,84 0,85 0,86 0,87 0,88 0,89 | 0,7881 | 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 | 0,8643 | 1,40 1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49 | 0,9192 | 1,70 1,71 1,72 1,73 1,74 1,75 1,76 1,77 1,78 1,79 | 0,9554 |
Для вероятности попадания на симметричный относительно математического ожидания интервал справедлива формула: P( |X - mX| < e ) = 2×Ф(e/s) - 1.
Центральные моменты нормального распределения удовлетворяют рекуррентному соотношению: mn+2 = (n+1)s2mn, n = 1, 2, ... . Отсюда следует, что все центральные моменты нечетного порядка равны нулю (так как m1 = 0).
Задача №2. Пусть Х ~ N(0, 1). Построить ФР и ПР. Найти Mo(X), Mе(X), A, E.
Случайные векторы
Упорядочная совокупность n случайных величин (СВ) Х1, Х2, ..., Хn, рассматриваемых совместно в данном опыте, называется n-мерной СВ или случайным вектором и обозначается 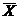 = (Х1, Х2, ..., Хn).
= (Х1, Х2, ..., Хn).
Функцией распределения (ФР) n-мерного случайного вектора называется функция n действительных переменных х1, x2, ..., xn, определяемая как вероятность совместного выполнения n неравенств: F(x1, x2, ... xn) = P{ X1 < x1, X2 < x2,..., Xn < xn}. В частности, для двумерного случайного вектора (X, Y) по определению ФР имеем: F(x, y) = P{X < x, Y < y}. ФР F (х, у) обладает следующими свойствами:
1. 0 £ F(x, у) £ 1;
2. F(x, у) - неубывающая функция своих аргументов;
3. 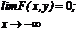
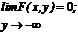
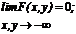
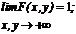
4. 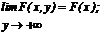
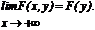
Свойство 4 обычно называют условием согласованности. Оно означает, что ФР отдельных компонент случайного вектора могут быть найдены предельным переходом из функции совместного распределения этих компонент. Вероятность попадания случайной точки на плоскости (X, Y) в прямоугольник со сторонами, параллельными осям координат, может быть вычислена с помощью ФР по формуле:
P{x1 £ X < x2, y1 £ Y < y2} = F(x1, y1)+ F(x2, y2)- F(x1, y2)- F(x2, y1).
Двумерный случайный вектор (X,Y) называется случайным вектором дискретного типа (СВДТ), если множество его возможных значений G(x, y) не более чем счетно. Ее закон распределения можно задать двумерной таблицей из перечня возможных значений пар компонент {(хi, yi) | (хi, yi) Î G(x, y)} и соответствующих каждой такой паре вероятностей pij = P{X = xi, Y = yj}, удовлетворяющих условию 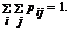
Двумерный случайный вектор (X, Y) называется случайным вектором непрерывного типа (СВНТ), если существует такая неотрицательная функция f(x, y) называемая плотностью распределения (ПР) вероятностей случайного вектора, что:
f(x, y) = 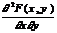 , тогда F(x, y) =
, тогда F(x, y) = 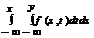 .
.
ПР вероятностей обладает следующими свойствами:
f(x, y) ³ 0, (x, y) Î R2;
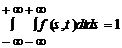 - условие нормировки.
- условие нормировки.
ПР вероятностей отдельных компонент случайного вектора выражаются в виде интегралов от совместной плотности:
f(x) = 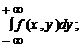 f(y) =
f(y) = 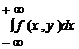 .
.
Вероятность попадания случайной точки в произвольную квадрируемую область S на плоскости определяется по формуле
P{(X, Y) Î S}= 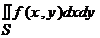 .
.
Условной плотностью распределения вероятностей случайной компоненты X при условии, что компонента Y приняла определенное значение у, называется функция f(x/y) действительной переменной х Î R: f(x/y) = f(x, y)/f(y). Аналогично определяется условная плотностью распределения вероятностей случайной компоненты Y при условии, что компонента X приняла определенное значение x: f(y/x) = f(x, y)/f(x). СВ X1, X2, ..., Хn называются независимыми (в совокупности), если для событий {Xi Î Bi}, i = 1, 2, ..., n, где B1, B2, ... Bn - подмножества числовой прямой, выполняется равенство: P{X1 Î B1, X2 Î B2, ... Xn Î Bn} = P{X1 Î B1}× P{X2 Î B2}× ... ×P{Xn Î Bn}.
Теорема: СВ X1, Х2, .... Хn независимы тогда и только тогда, когда в любой точке x = (x1, x2, ..., xn) имеет место равенство: F(x1, x2, ..., xn) = F(x1) × F (x2) × ... × F (xn) (или f(x1, x2, ..., xn) = f(x1) × f(x2) × ... × f(xn)).
