Равномерный закон распределения

Определение 5.2.15. Распределение вероятностей непрерывной случайной величины Х, принимающей свои значения из отрезка [a; b], называется равномерным, если ее плотность вероятности на этом отрезке постоянна и равна нулю вне его, причем

(5.2.35)

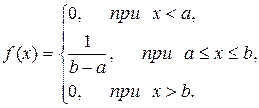
Пример 5.2.20. На отрезке [a; b] наугад указывают точку. Какова вероятность того, что эта точка окажется в левой половине отрезка?

○Пусть Х – случайная величина, равная координате выбранной точки. Х распределена равномерно (в этом и состоит точный смысл слов «наугад указывают точку»), а так как середина отрезка [a; b] имеет координату

(5.2.36)

,

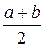то искомая вероятность равна, по формуле (5.2.19):

.●

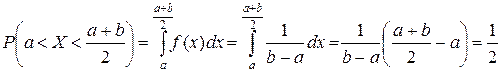Теорема 5.2.5. Функция распределения случайной величины Х, распределенной по равномерному закону, имеет вид

(5.2.37)

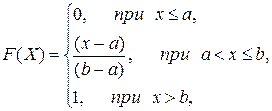
ее математическое ожидание

(5.2.38)

,

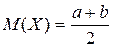а дисперсия

(5.2.39)

.

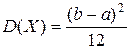Кривая распределения f(x) и график функции распределения F(x) случайной величины Х приведены на рис. 5.10 а, б.

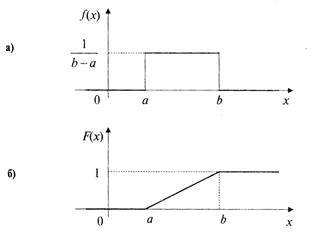
Рис. 5.10.

5.2.4.5. Нормальный закон распределения (закон Гаусса)

Нормальный закон распределения наиболее часто используют на практике. Это связано как с его относительной простотой, так и с тем, что многие случайные величины, формирование значений которых определяется большим количеством неконтролируемых факторов, каждый из которых вносит относительно небольшой вклад, имеют распределение, близкое к нормальному, например, рост человека, данные измерений, дальность полета снаряда и т.п..

Определение 5.2.16. Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами a и s, если ее плотность вероятности имеет вид:

(5.2.40)

.

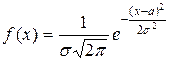Теорема 5.2.6.Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру а этого закона, т.е.

(5.2.41)

М(Х)=а,

(5.2.42)

а ее дисперсия – параметру s², т.е.

D(X)=s².

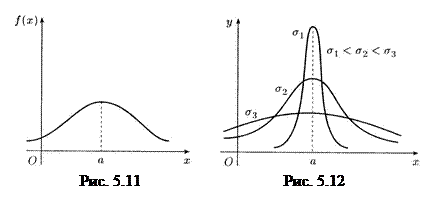
Кривую нормального закона распределения называют нормальной или гауссовой кривой. На рис. 5.11 приведен график функции (5.2.40). Обратим внимание на то, что нормальная кривая симметрична относительно прямой х=а, имеет максимум в точке х=а, равный 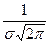. Значение ординаты максимума функции (5.2.40) убывает с возрастанием значения s (кривая «сжимается» к оси Ох) и возрастает с убыванием значения s (кривая «растягивается» в положительном направлении оси Оу), что отражено на рис. 5.12. Изменение значений параметра а (при неизменном значении s) не влияет на форму кривой. Таким образом, параметр а (он же математическое ожидание) характеризует положение центра, а параметр s² (он же дисперсия) – форму нормальной кривой.

Нормальный закон распределения случайной величины с параметрами а=0, s²=1 называется нормированным, а соответствующая нормальная кривая – нормированной. Плотность вероятности в случае такого распределения имеет вид:

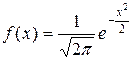– функция Гаусса.

Для этой функции составлена таблица (см. приложение 1) ее значений для положительных значений х (функция f(x) четная, т.е. f(x)= f(–x)).

Пусть случайная величина Х распределена по нормальному закону. Тогда вероятность того, что Х примет значение, принадлежащее интервалу (a; b), согласно формуле (5.2.19)

.

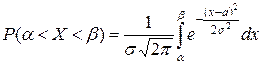Произведем в этом интеграле замену переменной, полагая .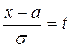

x	a	b
t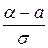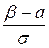

Тогда: х=а+st, dx=sdt , и

(5.2.43)

.

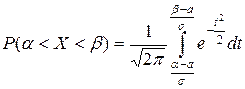Однако интеграл 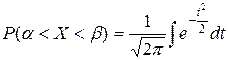не берется в элементарных функциях. Поэтому для вычисления этого интеграла вводится функция Лапласа[2]

(5.2.44)

,

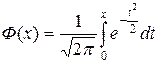Для этой функции составлена таблица (см. приложение 2) ее значений для положительных значений х, так как Ф(0)=0 и функция Ф(х) нечетная.

Тогда

(5.2.45)

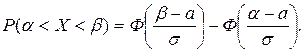
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины Х от ее математического ожидания по абсолютной величине меньше заданного положительного числа d, т.е. найти Р(|Х–а|<d). Это можно сделать по формуле

(5.2.46)

.

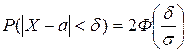Пример 5.2.21. Пусть случайная величина Х распределена по нормальному закону с параметрами а=20 и s=10. Найти Р(|Х–20|<3).

○ Используя формулу (5.2.46.), получим:

.

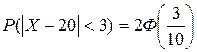По таблице приложения 2 находим: Ф(0,3)=0,1179.

Поэтому Р(|Х–20|<3)=2×0,1179=0,2358.●

[1] В литературе встречаются также термины: децили (под которыми понимаются квантили x_0,1, x_0,2, …, x_0,9) и процентили (квантили x_0,01, x_0,02, …, x_0,09)

[2] Пьер Лаплас (1749-1827) – французский математик и астроном.