Математическое ожидание дискретной случайной величины

Математическое ожидание дискретной случайной величины – это взвешенное среднее всех ее возможных значений, причем в качестве весового коэффициента берется вероятность соответствующего исхода. Вы можете рассчитать его, перемножив все возможные значения случайной величины на их вероятности и просуммировав полученные произведения. Математически если случайная величина обозначена как 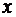, то ее математическое ожидание обозначается как 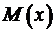или .

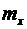Предположим, что 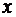может принимать 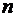конкретных значений 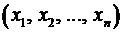и что вероятность получения 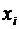равна 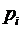. Тогда

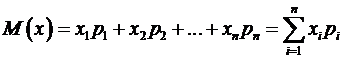. (A.1)

В случае с двумя костями величинами от 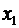до 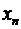были числа от 2 до 12. Математическое ожидание рассчитывается так:

.

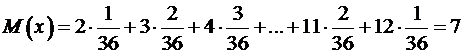Прежде чем пойти дальше, рассмотрим еще более простой пример случайной переменной – число очков, выпадающее при бросании лишь одной игральной кости.

В данном случае возможны шесть исходов: 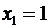, , 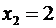…, 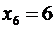. Каждый исход имеет вероятность 1/6, поэтому здесь

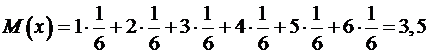. (A.2)

В данном случае математическим ожиданием случайной переменной является число, которое само по себе не может быть получено при бросании кости.

Математическое ожидание случайной величины часто называют ее средним по генеральной совокупности. Для случайной величины 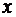это значение часто обозначается как .

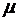Математические ожидания функций дискретных случайных переменных

Пусть 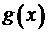– некоторая функция от 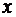. Тогда 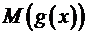– математическое ожидание 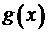записывается как

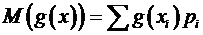, (A.3)

где суммирование производится по всем возможным значениям 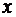. В табл. A.3 показана последовательность практического расчета математического ожидания функции от .

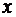Таблица A.3

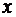	Вероятность	Функция от	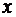Функция, взвешенная по вероятности
…	…	…	…
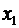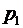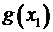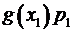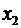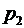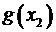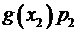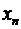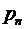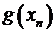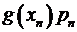Всего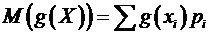

Предположим, что 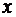может принимать 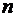различных значений от 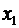до 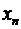с соответствующими вероятностями от 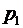до 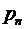. В первой колонке записываются все возможные значения 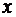. Во второй – записываются соответствующие вероятности. В третьей колонке рассчитываются значения функции для соответствующих величин 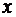. В четвертой колонке перемножаются числа из колонок 2 и 3. Ответ приводится в суммирующей строке колонки 4.

Рассчитаем математическое ожидание величины 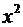. Для этого рассмотрим пример с числами, выпадающими при бросании одной кости. Использовав схему, приведенную в табл. A.3, заполним табл. A.4.

Таблица A.4

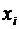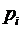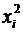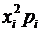	1/6		0,167
	1/6		0,667
	1/6		1,500
	1/6		2,667
	1/6		4,167
	1/6		6,000
Всего	15,167

В четвертой ее колонке даны шесть значений 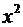, взвешенных по соответствующим вероятностям, которые в данном примере все равняются 1/6. По определению, величи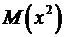на равна 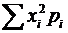, она приведена как сумма в четвертой колонке и равна 15,167.

Математическое ожидание 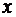, как уже было показано, равно 3,5, и 3,5 в квадрате равно 12,25. Таким образом, величина 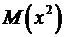не равна 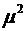, и, следовательно, нужно аккуратно проводить различия между 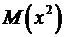и 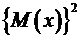.