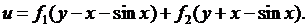Нахождение общих решений некоторых дифференциальных уравнений с частными производными

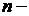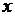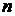Как известно, общее решение обыкновенного дифференциального уравнения го порядка представляется функцией от независимой переменной и произвольных постоянных интегрирования :

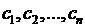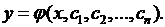(4.1)

Зная это общее решение, можно решить ту или иную задачу, например, задачу Коши, определяя соответствующим образом постоянные .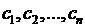

Для дифференциальных уравнений с частными производными невозможно указать единого вида общего решения, аналогичного (4.1), но можно находить его в отдельных частных случаях путем непосредственного интегрирования их канонических форм. Этот факт мы проиллюстрируем на некоторых примерах уравнений.

Пример 4.1. Найти общее решение уравнения колебаний струны

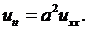(4.2)

Решение. Сначала приведем его к каноническому виду. Характеристическое уравнение (3.9) в нашем случае имеет вид:

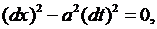
а его общие решения -

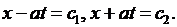
Следовательно, в соответствии с (3.12) за новые переменные 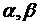берем

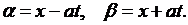(4.3)

Так как

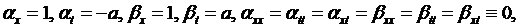
то из формул (3.4) получим

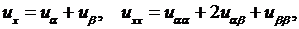
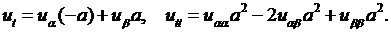
Подставив эти значения 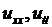в уравнение (4.2), получим канонический вид уравнения колебаний струны

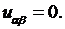(4.4)

Найдем общее решение уравнения (4.4). Обозначим

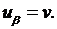(4.5)

Тогда уравнение (4.4) примет вид

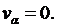(4.6)

Уравнению (4.6) удовлетворяет любая функция, не зависящая от 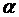. Следовательно,

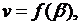(4.7)

где 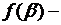произвольная функция переменной 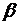. Подставляя (4.7) в (4.5), имеем

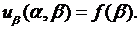(4.8)

Проинтегрируем уравнение (4.8) по переменной 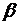, рассматривая 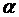как параметр и беря постоянную интегрирования в виде произвольной функции этого параметра. В результате получим

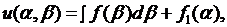
где 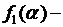произвольная функция 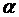. Обозначив 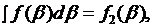окончательно получим

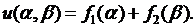
Возвращаясь к старым переменным 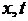с помощью соотношений (4.3), будем иметь

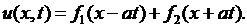(4.9)

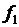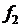Нетрудно проверить, что функция (4.9) есть решение уравнения (4.2), если и - произвольные дважды непрерывно дифференцируемые функции.

Выражение (4.9) является общим решением уравнения свободных колебаний струны (4.2).

Пример 4.2.Найти общее решение уравнения

.

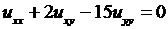Решение. Сначала приведем его к каноническому виду. Составим ха-

рактеристическое уравнение и решаем его:

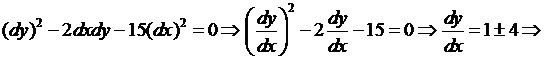
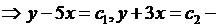характеристики уравнения.

Следовательно, в соответствии с (3.12) за новые переменные 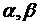берем

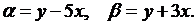
Так как

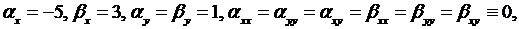
то из формул (3.4) получим

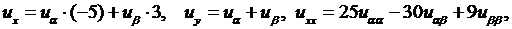
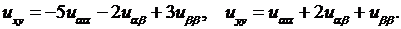
Подставим эти значения 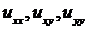в уравнение:

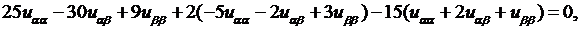
откуда получим его канонический вид: 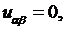общее решение которого дается формулой (см. пример 4.1) 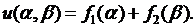Возвращаясь

к старым переменным 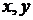, получаем окончательно

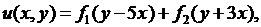
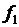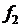где и - произвольные дважды непрерывно дифференцируемые функции.

Пример 4.3.Найти общее решение уравнения

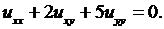
Решение. Составим характеристическое уравнение и решаем его:

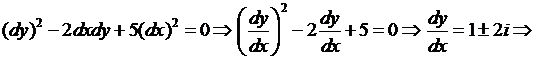
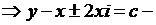комплексно сопряженные характеристики уравнения.

Поэтому за новые переменные 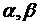берем

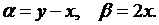
Так как

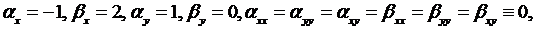
то из формул (3.4) получим

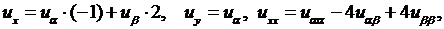
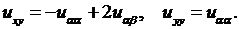
Подставим эти значения 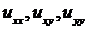в уравнение:

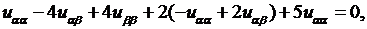
откуда получим его канонический вид: 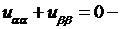уравнение Лапласа.

Из теории аналитических функций комплексного переменного известно, что действительная и мнимая части аналитической функции удовлетворяют уравнению Лапласа. Следовательно, общее решение уравнения Лапласа можно записать в виде

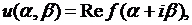
где 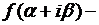произвольная аналитическая функция аргумента 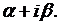Возвращаясь к старым переменным 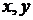, получаем общее решение исходного уравнения в виде

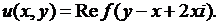
Пример 4.4.Найти общее решение уравнения

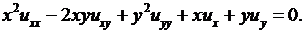
Решение. Составим характеристическое уравнение и решаем его:

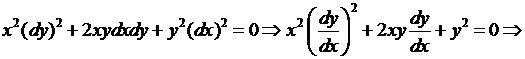
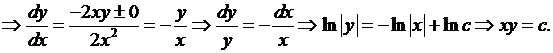
Итак, характеристическое уравнение имеет одно семейство действительных характеристик. Положим 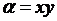, а за 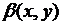в соответствии с вышесказанным возьмем любую дважды непрерывно дифференцируемую функцию, для которой якобиан 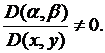Например, пусть 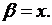Тогда

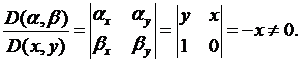
Так как

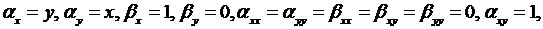
то подставляя эти значения производных в (3.4), получаем

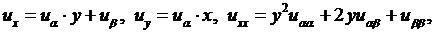
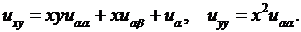
Теперь эти выражения производных внесем в исходное уравнение:

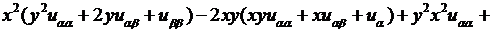
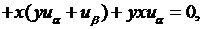
откуда 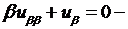канонический вид уравнения. Решаем его. Обозначим 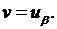Тогда уравнение примет вид: 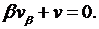Это есть уравнение с разделяющимися переменными, при этом переменная 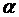считается параметром. Получаем

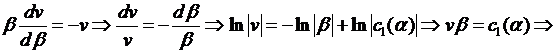
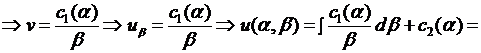
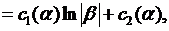
где 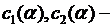постоянные интегрирования, представляющие собой произвольные функции переменной 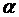. Возвращаясь к старым переменным 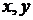, получаем общее решение исходного уравнения в виде

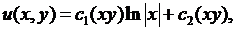
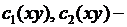произвольные дважды непрерывно дифференцируемые функции аргумента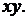

Задачи

Найти общее решение уравнений:

4.1. 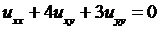; 4.2. ;

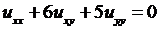4.3. 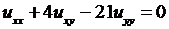; 4.4. ;

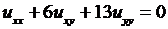4.5. 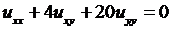; 4.6. ;

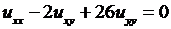4.7. ;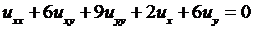

4.8. ;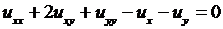

4.9.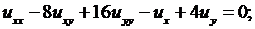

4.10.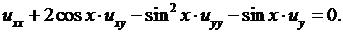

Ответы:

4.1. 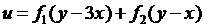; 4.2. ;

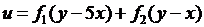4.3. 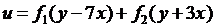; 4.4. ;

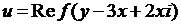4.5. 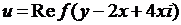; 4.6. ;

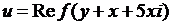4.7. 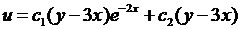; 4.8. ;

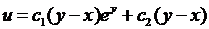4.9. ;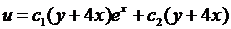

4.10.