Интегралы от функций, содержащих квадратный трехчлен
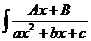 dx;
dx; 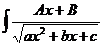 dx;
dx; 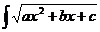 dx.
dx.
Для отыскания этих интегралов сначала выделяют полный квадрат из трехчлена, в результате чего он преобразуется в квадратный двучлен
ах2 + bx + с = а (х2 + 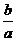 х +
х + 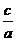 ) = а [(х +
) = а [(х + 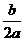 )2 +
)2 + 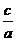 -
- 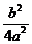 ] = а [(х +
] = а [(х + 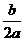 )2 ± k2].
)2 ± k2].
В дальнейшем интегралы указанных видов вычисляются методом замены переменной или выделением целой части.
Пример. Найти интеграл 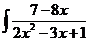 dx.
dx.
Решение.
Выделим из квадратного трехчлена полный квадрат
2х2 – 3х + 1 = 2(х2 – 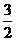 х +
х +  ) = 2[(х –
) = 2[(х – 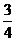 )2 +
)2 +  –
– 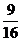 ] = 2[(х –
] = 2[(х – 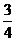 )2 –
)2 – 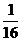 ].
].
Положим х – 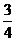 = t тогда dt = dx. Проведем замену переменной.
= t тогда dt = dx. Проведем замену переменной.
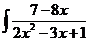 dx =
dx = 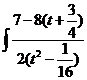 dt =
dt = 
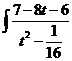 dt =
dt = 
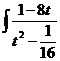 dt =
dt = 
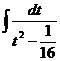 - -
- - 
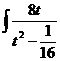 dt =
dt =  ∙
∙ 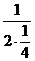 ∙ln
∙ln 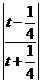 -
-  ∙4
∙4 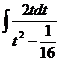 = ln
= ln 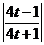 - 2 ln|t2 -
- 2 ln|t2 - 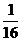 | = ln
| = ln 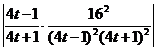 = ln
= ln 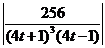 .
.
Возвращаясь к переменной х, находим:
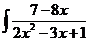 dx = ln
dx = ln 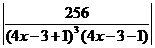 = ln
= ln 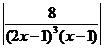 + С.
+ С.
٭ ٭
٭
201. Найти интегралы:
а) 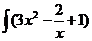 dx; с)
dx; с) 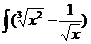 dx;
dx;
b) 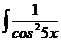 dx; d)
dx; d) 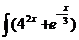 dx.
dx.
202. Найти интегралы:
а) 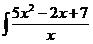 dx; с)
dx; с) 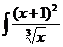 dx;
dx;
b) 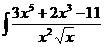 dx; d)
dx; d) 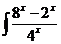 dx.
dx.
203. Найти интегралы:
а) 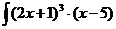 dx; с)
dx; с) 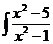 dx;
dx;
b) 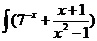 dx; d)
dx; d) 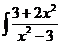 dx.
dx.
204. Найти интегралы:
а) 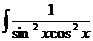 dx; с)
dx; с) 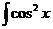 dx;
dx;
b) 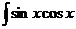 dx; d)
dx; d) 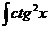 dx.
dx.
205. Найти интегралы методом замены переменной:
а) 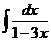 ; с)
; с) 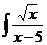 dx;
dx;
b) 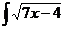 dx; d)
dx; d) 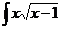 dx.
dx.
206. Найти интегралы методом замены переменной:
а) 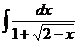 ; с)
; с) 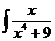 dx;
dx;
b) 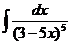 dx; d)
dx; d) 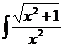 dx.
dx.
207. Найти интегралы методом замены переменной:
а) 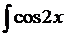 dx; с)
dx; с) 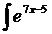 dx;
dx;
b) 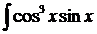 dx; d)
dx; d) 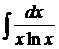 .
.
208. Найти интегралы путем интегрирования по частям:
а) 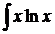 dx; с)
dx; с) 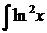 dx;
dx;
b) 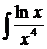 dx; d)
dx; d) 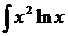 dx.
dx.
209. Найти интегралы путем интегрирования по частям:
а) 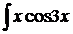 dx; с)
dx; с) 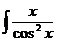 dx;
dx;
b) 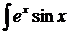 dx; d)
dx; d) 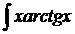 dx.
dx.
210. Найти интегралы путем интегрирования по частям:
а) 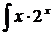 dx; с)
dx; с) 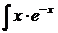 dx;
dx;
b) 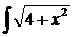 dx; d)
dx; d) 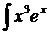 dx.
dx.
211. Найти интегралы:
а) 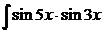 dx; с)
dx; с) 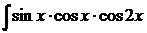 dx;
dx;
b) 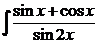 dx; d)
dx; d) 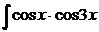 dx.
dx.
212. Найти интегралы:
а) 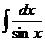 , подстановка cos x = t;
, подстановка cos x = t;
b) 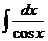 , подстановка sin x = t.
, подстановка sin x = t.
213. Найти интегралы, используя подстановку 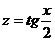 :
:
а) 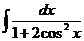 ; с)
; с) 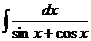 ;
;
b) 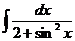 ; d)
; d) 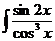 dx.
dx.
214. Найти интегралы:
а) 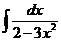 ; с)
; с) 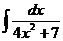 ;
;
b) 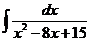 ; d)
; d) 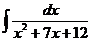 dx.
dx.
215. Найти интегралы:
а) 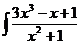 dx; с)
dx; с) 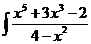 dx;
dx;
b) 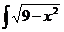 dx; d)
dx; d) 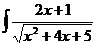 dx.
dx.
§2. Определенный интеграл
Понятие определенного интеграла. Простейшие свойства определенного интеграла
Интегралом от а до b функции f(x) называется приращение первообразной F(х) этой функции, т.е. F(b) – F(а).
Интеграл от а до b функции f(x) обозначается 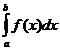 . Числа а и b называются пределами интегрирования, а – нижним, b – верхним; отрезок [а; b]– отрезком интегрирования.
. Числа а и b называются пределами интегрирования, а – нижним, b – верхним; отрезок [а; b]– отрезком интегрирования.
Простейшие свойства определенного интеграла
1. При перестановке пределов меняется знак интеграла
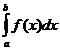 = -
= - 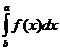 .
.
2. Интеграл с одинаковыми пределами равен 0
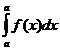 = 0.
= 0.
3. Отрезок интегрирования можно разбивать на части
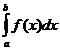 =
= 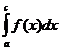 +
+ 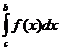 .
.
4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых.
5. Постоянный множитель можно выносить за знак интеграла.
Формула Ньютона-Лейбница
Для вычисления определенного интеграла, когда можно найти соответствующий неопределенный интеграл, служит формула Ньютона – Лейбница.
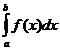 =
= 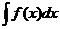
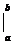 = F(х)
= F(х) 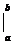 = F(b) – F(а).
= F(b) – F(а).
Определенный интеграл равен разности значений неопределенного интеграла при верхнем и нижнем пределах интегрирования.
Пример. Вычислить интеграл 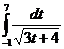 .
.
Решение.
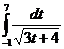 =
= 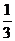
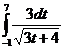 =
= 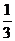
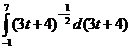 =
= 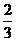
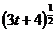
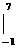 =
= 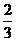
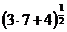 - -
- - 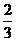
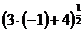 =
= 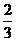 ∙5 -
∙5 - 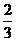 ∙1 =
∙1 = 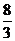 = 2
= 2 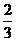 .
.
Ответ: 2 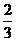 .
.
Площадь плоской фигуры
Площадь всякой плоской фигуры, отнесенной к прямоугольной системе координат, может быть составлена из площадей криволинейных трапеций, прилежащих к оси Ох или оси Оу.
Площадь криволинейной трапеции вычисляется по формуле:
S = 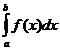 = F(b) – F(а).
= F(b) – F(а).
В том случае, когда непрерывная функция f(x) ≤ 0 на отрезке [а; b], площадь соответствующей криволинейной трапеции вычисляется по формуле
S = - 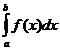 = F(а) – F(b).
= F(а) – F(b).
Если функция f(x) непрерывна на отрезке [а; b] и принимает на данном отрезке как положительные, так и отрицательные значения, то отрезок интегрирования разбивается на такие части, в каждой из которых функция
|
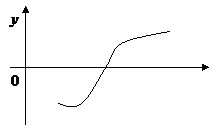

Рис. 13
| |||
 | |||
|
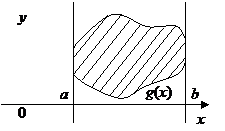
Рис. 14.
Пример. Вычислить площадь фигуры, ограниченной линиями х = 4, у = х2 – 4х + 6, у = 2.
Решение.
Найдем пределы интегрирования - точки пересечения данных линий. Имеем а = 2, b = 4, причем х2 – 4х + 6 ≥ 2. следовательно площадь фигуры, ограниченной данными линиями равна
S = 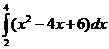 –
– 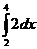 =
= 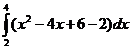 =
= 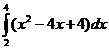 =
= 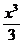 –
– 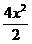 +4х
+4х 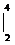 = =
= = 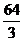 – 32 + 16 – (
– 32 + 16 – ( 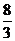 – 8 + 8) =
– 8 + 8) = 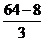 – 16 = 18
– 16 = 18 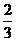 – 16 = 2
– 16 = 2 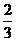 (кв.ед.)
(кв.ед.)
Ответ: S = 2 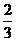 кв.ед.
кв.ед.
Объем тела вращения
Если тело образуется при вращении вокруг оси Ох криволинейной трапеции прилежащей коси Ох, его объем определяется по формуле
V = 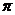
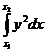 , (х1 < х2).
, (х1 < х2).
Если тело образуется при вращении вокруг оси Оу криволинейной трапеции прилежащей к оси Оу, его объем определяется по формуле
V = 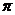
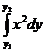 , (у1 < у2).
, (у1 < у2).
Пример. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями: у2 = 2рх, х = а вокруг оси Ох.
Решение.
V = 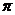
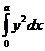 =
= 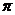
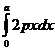 =
= 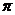 рх2
рх2 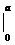 =
= 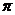 ра2.
ра2.
Ответ: V = 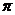 ра2.
ра2.
٭ ٭
٭
216. Вычислить определенные интегралы:
а) 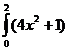 dx; с)
dx; с) 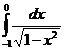 ;
;
b) 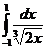 dx; d)
dx; d) 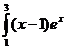 dx.
dx.
217. Вычислить определенные интегралы:
а) 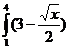 dx; с)
dx; с) 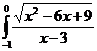 dx;
dx;
b) 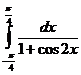 ; d)
; d) 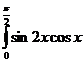 dx.
dx.
218. Вычислить определенные интегралы:
а) 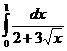 ; с)
; с) 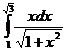 ;
;
b) 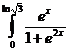 dx; d)
dx; d) 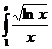 dx.
dx.
219. Найти площадь фигуры, ограниченной параболой у = 6х - 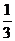 х2 и осью абсцисс.
х2 и осью абсцисс.
220. Вычислить площадь фигуры, ограниченной линиями:
а) у = 2х + 3, у = 0, х = -1, х = 2;
b) у = 5х – 3х2, у = 0;
с) у =  , у = 0, х = 1, х = 3;
, у = 0, х = 1, х = 3;
d) у = 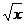 , у = 3, х = 0.
, у = 3, х = 0.
221. Вычислить площадь фигуры, ограниченной линиями:
а) у = 2sin х, у = 0, х = - π, х = 0;
b) у = 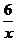 , у = 0, х = 1, х = 6;
, у = 0, х = 1, х = 6;
с) у =  х – 1, у = 0, х = 0, х = 6;
х – 1, у = 0, х = 0, х = 6;
d) у = 2х2 – 2, у = 0, х = 2.
222. Вычислить площадь фигуры, ограниченной линиями:
а) у = х2, у = 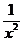 , у = 0, х = 3;
, у = 0, х = 3;
b) у = cos x, у = 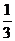 х + 1, х = -2, х =
х + 1, х = -2, х = 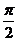 ;
;
с) у = х2 – 4, у = х – 2;
d) у = sin х, у = cos x .
223. Вычислить площадь фигуры, ограниченной линиями:
а) х + 4у – 9 = 0, 2х – 3у + 4 = 0,3х + у – 16 = 0;
b) у =  , у = - х2 + 2х + 0,5, у = 0,5х + 0,5;
, у = - х2 + 2х + 0,5, у = 0,5х + 0,5;
с) у = -х2 – 2х + 7, у = -х2 – 4х + 7, у = -4х + 6;
d) у = sin х, у = 2sin x, х = 0, х = π.
224. Вычислить объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями:
а) х2 + у2 = 9, х = -1;
b) у =  , х =
, х =  , х = 2;
, х = 2;
с) у = х2 – 3, х = -2, х = 3;
d) у = sin х, х = 0, х = π.
225. Вычислить объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями:
а) у = 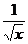 , х = 1, х = е;
, х = 1, х = е;
b) у = ln x, х = 1, х = е;
с) у = -х2 – 2х – 3, х = -1, х = 3;
d) у = sin 2х, х = 0, х = 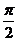 .
.
226. Вычислить объем тела, образованного вращением вокруг оси абсцисс эллипса 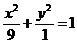 .
.
227. Вычислить объем тела, образованного вращением вокруг оси абсцисс плоской фигуры, ограниченной параболами у = х2 и х = у2.
228. Вычислить объем тела, образованного вращением вокруг оси абсцисс плоской фигуры, ограниченной окружностью х2 + у2 = 4 и прямой у = х.
229. Вычислить объем тела, образованного вращением вокруг оси абсцисс плоской фигуры, ограниченной кубической параболой у = х3 и параболой х = у2.
230. Вычислить объем тела, образованного вращением вокруг оси абсцисс плоской фигуры, ограниченной кривой у = sin 2х и прямой у = 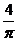 х.
х.
Глава 6. Дифференциальные уравнения

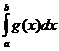 . S =
. S = 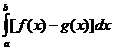 .
.