Экономическая интерпретация переменных двойственных задач.

Пусть Y_i – теневая цена (оценка i-того вида ресурса). Эта оценка важна только для оптимального плана.

До тех пор, пока прибыль меньше оценки суммарной стоимости затрат, решение остается неоптимальными, и лишь тогда, когда прибыль совпадает с оценкой общей стоимости ресурсов, затраченных на производство единицы данного вида продукции, план остается оптимальным.

1. Если Z_j-С_j<0, то следует увеличить производство продукции j-того вида, а так как Z_j<С_j цена реализации больше приведенных издержек, то при выборе вектора, вводимого в базис, это означает, что увеличиваем производство продукции наиболее «дешевой» при заданном способе производства относительно цены реализации. Поэтому выбираем вектор с наименьшей отрицательной оценкой.

2. Если Z_j-C_j>0, 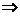x_j – не базисная переменная и в оптимальном плане x_j=0, т.е. производство продукции j-вида не предусмотрено в оптимальном плане.

Если в оптимальном плане y_i>0, то i-тое ограничение выполняется в форме равенства: 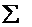a_ijx_j=b_i и, следовательно, соответствующая остаточная переменная будет равна 0. Величине Z_j-С_j соответствует избыточная переменная двойственной задачи, которую обозначим через V_j: V_j=Z_j-С_j , а S_i – остаточная переменная прямой задачи. Тогда условие 1 и 2 можно выразить в виде:

Если V_j>0, то x_j=0

Если Y_i>0, то S_i=0

или в более компактной форме это записывается:

V_jX_j=Y_iS_i=0, что является одной из форм второй теоремы двойственности и называется теоремой о дополняющей нежесткости.

Пример: Исследование оптимальных решений с помощью двойственных оценок (экономический анализ):

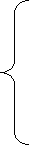задача Z=40x₁+60x₂+50x₃ 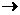max

8x₁+6x₂+5x₃≤60

4x₁+4x₂+6x₃≤30

5x₁+5x₂+8x₃ ≤90

x₁,x₂,x₃ 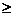0

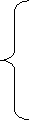W=60y₁+30y₂+90y₃ 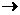min

8y₁+4y₂+5y₃≤40

6y₁+4y₂+5y₃≤60

5y₁+6y₂+8y₃ ≤50

Б	СБ	В	A1	A2	A3	A4	A5	А6
С1=40	С2=60	С3=50	С4=0	С5=0	С6=0
A4					-4		-3/2
A2		15/2			3/2		1/4
А6		105/2			1/2		-5/4
Zj-Cj

x^*=(0, 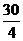,0) Z_max=450

y^*=(0,15,0)

1. Оценка ресурса показывает насколько изменится оптимальное значение целевой функции (это значение целевой функции на оптимальном плане), если объем соответствующего ресурса увеличить на единицу.

2. Ресурс дефицитный для данного оптимального плана, если он полностью используется при производстве согласно этому плану.

3. В оптимальном плане включается производство только тех видов продукции, оценки ресурсов на производство которых совпадают с ценой реализации соответствующих видов продукции.

1. Оценки первого и третьего вида ресурсов в оптимальном плане равны нулю. Следовательно, изменение объемов этих ресурсов (в определенных границах) не изменит объема выпуска продукции и, следовательно, оптимальное значение прибыли . Оценка изменения единиц второго ресурса равна 15, и, следовательно, изменение объема данного ресурса на единицу (при увеличение) приведет к увеличению оптимального значения целевой функции на 15 единиц.

2. Первый и третий ресурсы недефицитны (для данного оптимального плана). Посчитаем расход второго вида ресурса при оптимальном плане. Для этого во второе ограничение прямой задачи подставим значение оптимального плана. Оно выполняется как тождество (второй ресурс используется полностью). При подстановке в первое и третье ограничения прямой задачи значения оптимального плана они выполняются как строгие неравенства. Причем разность значений левых и правых частей равна соответственно.

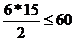45<60 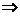60-45=15

Это соответствует значению остаточной переменной прямой задачи в оптимальном плане.

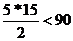
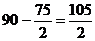
Это соответствует значению остаточной переменной третьего ограничения прямой задачи в оптимальном плане.

3. В оптимальном плане не предусмотрен выпуск продукци первого и третьего вида.

Подсчитаем оценку ресурсов, израсходованных на производство единицы продукции третьего вида. Для этого подставим значение оценок оптимального плана в третье ограничение двойственной задачи. Получаем 90>50, разность между значениями левой и правой частей равна 40, что соответствует превышению затратной оценки ресурсов на производство единицы продукции третьего вида над ценой ее реализации. Фактически выражение Z_j-C_j численно равно превышению затратной оценки над ценой реализации. Аналогично объясняется значение Z₁-C₁=20.

Оценка второго вида ресурсов положительна, следовательно, данный ресурс является дефицитным (полностью используется при оптимальном плане), и означает, что при увеличении данного ресурса на единицу оптимальное значение целевой функции возрастет на 15 единиц, и это будет достигнуто за счет увеличения расходов первого вида ресурса на 3/2 единицы и третьего вида ресурса на 5/4 единицы (такое количество следует вычитать из соответствующих значений остаточных переменных для данных ограничений прямой задачи) и при этом должно произойти увеличение выпуска продукции второго вида на ¼ единицы.

Теорема 8.1

В оптимальном плане двойственной задачи Y^* значение переменной y^*_i численно равно частной производной оптимального значения целевой функции (производная значения целевой функции берется как от функции объема ресурсов) Z_max (b₁…b_m) по данному аргументу.

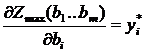
Изменение объемов дефицитных ресурсов приводит к изменению значений целевой функции на оптимальном плане. И это изменение определяется величиной y^*_i и характеризуется лишь в случае, когда данное значение положительно. Эта характеристика скорости изменения (интенсивности) оптимального значения целевой функции в зависимости от интенсивности изменения объемов ресурсов. При расширении производства требуется определить выбор тех видов ресурсов, увеличение объемов которых позволит наиболее эффективно организовать производство данного вида продукции. Для данной задачи расширение возможно только второго вида.

Раздел II.

Специальные задачи ЛП