Теоретическая механика. Статика. Системы сил, их условия и уравнения равновесия. Применение уравнений равновесия к решению задач.
Введение
Техническая механикасостоит из трех частей: 1. Теоретическая механика; 2. Сопротивление материалов; 3. Детали машин, и является теоретической базой для изучения специальных дисциплин.
Часть 1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Теоретическая механика – это наука, которая изучает законы движения тел и общие свойства движения. Состоит из трех разделов: статика; кинематика; динамика.
Допущенияпри изучении теоретической механики:
1. Материальная точка – это материальное тело, имеющее массу, размерами и формой которого в условиях данной задачи можно пренебречь.
2. Абсолютно твердое тело - это материальное тело, расстояния между любыми двумя точками которого остаются неизменными.
МОДУЛЬ 1.
Рис.1 Расчетная схема
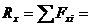
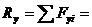
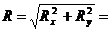
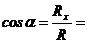
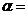
Задача 2. Определить проекцию равнодействующей на ось х (рис.1)
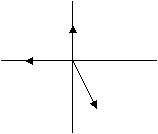
Рис.1 Расчетная схема
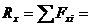
Условие равновесия ПССС: 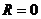 -Равнодействующая равна нулю.
-Равнодействующая равна нулю.
Геометрическое условие равновесия:Замкнутость силового многоугольника.
Аналитическое условие равновесия: 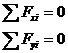 - уравнения равновесия
- уравнения равновесия
Для равновесия ПССС необходимо и достаточно, чтобы алгебраические суммы проекций составляющих сил на координатные оси плоскости были порознь равны нулю.
Задача 3. Составить уравнения равновесия плоской системы сходящихся сил (рис.1).
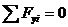
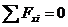
Рис. 1 Расчетная схема
Задача 4. Определить реакции стержней (рис.1) аналитическим способом и проверить геометрическим.
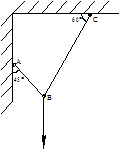
Рис.1 Условие задачи
1. Определить реакции стержней аналитическим способом.
1.1 Выделить объект равновесия – точка В.Указать активную нагрузку (в данной задаче 100 кН). Заменить стержни реакциями F1 и F2.
1.2 Определить угол между реакциями (в данном примере 75 о - угол острый)
1.3 Совместить ось у с одной из реакций, например, F2. Провести ось х.
1.4 Определить угол между осью у и активной нагрузкой (в данном примере 30 о )
Примечание: Выполненные в п.п. 1.1 – 1.4 действия называются составлением расчетной схемы для аналитического способа (рис.2)
1.5 Составить уравнения равновесия и определить неизвестные реакции.
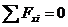
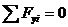
Рис. 2 Расчётная схема.
2. Определить реакции стержней геометрическим способом (рис.3)
2.1 Выделить объект равновесия – точка В. Указать активную нагрузку. Заменить стержни реакциями F1 и F2.
2.2 Построив параллелограмм, выделить в нем замкнутый силовой треугольник. Направления стрелок всех сил в треугольнике должны быть по направлению активной нагрузки.
1.3 Обозначить углы в треугольнике и силы.
Примечание: Выполненные в п.п. 1.1 – 1.3 действия называются составлением расчетной схемы для геометрического способа (рис.2)
1.4 Составить теорему синусов и определить неизвестные реакции
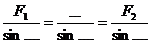
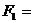
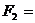
Рис.3 Расчётная схема.
Задача 5. Определить реакции стержней (рис.1) аналитическим способом и проверить геометрическим.
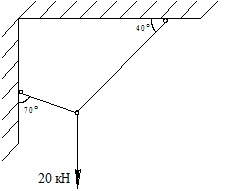
Рис.1 Условие задачи
Примечание: Порядок решения задачи аналогичен задаче 4.
- Определить реакции стержней аналитическим способом (рис.2)
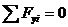
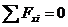
Рис. 2 Расчётная схема.
- Определить реакции стержней геометрическим способом (рис.3)
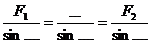
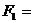
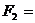
Рис.3 Расчётная схема.
Задача 6. Определить реакции стержней (рис.1) аналитическим способом и проверить геометрическим.
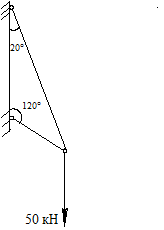
Рис.1 Условие задачи
Примечание: Порядок решения задачи аналогичен задаче 4.
1. Определить реакции стержней аналитическим способом (рис.2)
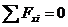
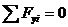
Рис. 2 Расчётная схема.
2. Определить реакции стержней геометрическим способом (рис.3)
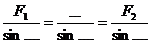
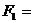
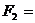
Рис.3 Расчётная схема.
Приведение ПСПРС к центру
Рис. 2 К приведению ПСПРС к центру
Главный вектор Rо ПСПРС равен геометрической сумме составляющих сил системы и приложен в центре приведения (рис.2). После приведения - это равнодействующая ПССС, поэтому модуль определяется по формуле: Rо= 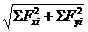 , а направление по направляющему косинусу
, а направление по направляющему косинусу 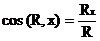 . Главный момент Мо ПСПРС равен алгебраической сумме моментов составляющих сил относительно центра приведения. После приведения - это момент приведенной системы пар сил М о = Мрез.=
. Главный момент Мо ПСПРС равен алгебраической сумме моментов составляющих сил относительно центра приведения. После приведения - это момент приведенной системы пар сил М о = Мрез.= 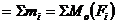
Условие равновесия ПСПРС: R = 0, М 0 = 0. Главный вектор и главный момент равны нулю.
Зная, как определяются главный вектор и главный момент, имеемуравнения равновесия:
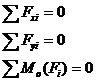 - Уравнения равновесия (форма 1равновесия)
- Уравнения равновесия (форма 1равновесия)
Для равновесия ПСПРС необходимо и достаточно, чтобы алгебраические суммы проекций составляющих сил на координатные оси плоскости и алгебраическая сумма моментов составляющих сил относительно произвольной точки плоскости были порознь равны нулю.
Для системы параллельных сил (это частный случай ПСПРС) существует вторая форма:

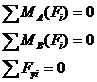 - Уравнения равновесия (форма 2 равновесия)
- Уравнения равновесия (форма 2 равновесия)
Для равновесия системы параллельных сил необходимо и достаточно, чтобы алгебраические суммы моментов составляющих сил относительно двух произвольных точек плоскости и алгебраическая сумма проекций составляющих сил на координатную ось, не совпадающую с данными точками плоскости, были порознь равны нулю.
Рис.1 Расчетная схема балки
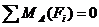
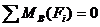
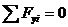
7.2 Примечание: Активные нагрузки – две силы и момент. Связь – шарниры. 2 форма равновесия
Рис.2 Расчетная схема балки
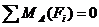
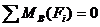
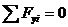
7.3 Примечание: Активные нагрузки – сила расположена симметрично относительно опор. Можно воспользоваться правилом коромысла: численное значение реакций равно половине активной нагрузки, а направление реакций противоположно направлению активной нагрузки.
Рис.2 Расчетная схема балки
YА = YВ =
7.4 Примечание: Активные нагрузки – одна сила под углом. Связь – жесткая заделка.
1 форма равновесия
Рис.1 Расчетная схема балки
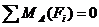
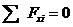
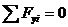
7.5 Примечание: Активные нагрузки – одна сила. Связь – жесткая заделка. 2 форма равновесия
Рис.2 Расчетная схема балки
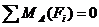
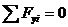
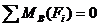
РАСЧЕТНО-ГРАФИЧЕСКИЕ РАБОТЫ ПО ТЕХНИЧЕСКО МЕХАНИКЕ
Примечание: Работы должны быть оформлены в соответствии с требованиями ГОСТ 2.105-79 и ГОСТ 2.106 -68, на листах формата А4, условия работ – с основной надписью по форме 2, решение – по форме 2а.
РГР №1 «Расчеты стержней при растяжении, сжатии»
Примечание: Для защиты модуля 1 оформить условие РГР №1 и выполнить п.п.1, 2 задачи 2.
Задача 1. Определить деформации стержней (указать в условии)
Решение: 1.1 Для стального (Е = 2٠105 МПа) стержня (рис.1) постоянного поперечного сечения (А= см2):
а) Продольные силы на участках:
N1=
N2=
N3=
N4=
б) Опасный участок: Nmax =
в) Напряжение на опасном участке:
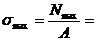
Рис.1 Расчетная схема стержня и эпюра
продольных сил
г) Удлинение стержня 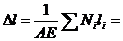
1.2 Для стального (Е = 2٠10 5 МПа) стержня (рис.2) непостоянного поперечного сечения:
а) Продольные силы на участках:
N1=
N2=
N3= 
б) Напряжения на участках:
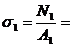
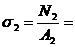
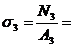
в) Опасный участок: 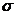 max =
max =
г) Удлинение стержня Рис.2 Расчетная схема бруса и
эпюры продольных сил и нормальных напряжений.
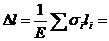
Задача 2 Для стержневой системы (рис.3) определить реакции стержней и подобрать соответствующие номера профилей (два равнополочных уголка). Определить процент пере- или недогрузки наиболее нагруженного стержня при принятых стандартных размерах сечения, если допускаемое напряжение [σ] = 150 МПа.
Рис.3 Условие задачи
Решение:
1. Определить аналитическим способом реакции в стержнях (рис.4).
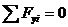
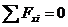
Рис.4 Расчетная схема.
2. Проверить геометрическим способом реакции в стержнях (рис.5).
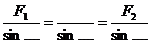
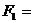
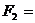
Рис.5 Расчетная схема.
3. Указать деформации стержней: 1 - 2 -
Примечание: Деформации в стержнях вызывают усилия, а они противоположны по направлению реакциям.
Далее считать F1 = N1 , F2 = N2 .
4. Определить требуемую площадь поперечного сечения для двух уголков.
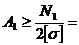
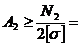
5. Подобрать номера уголков по ГОСТ 8509 – 86 Равнополочные уголки.
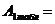 см2 , № t = мм
см2 , № t = мм
 см2 , № t = мм
см2 , № t = мм
6. Определить напряжение в стержнях для подобранных сечений.
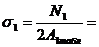
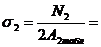
7. Определить процент перегрузки (недогрузки) наиболее нагруженного стержня.
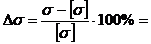
МОДУЛЬ 2.
Вариант 1. Заданы параметры всех передач привода
Задача 15. Выполнить силовой и кинематический расчет привода (рис.1), если Pдв = 5 кВт, nдв = 980 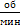 , η31= 0,97, η32 = 0,98, ηЦ = 0,95 (КПД муфты и подшипников условно включены в КПД передач для упрощения решения задачи)
, η31= 0,97, η32 = 0,98, ηЦ = 0,95 (КПД муфты и подшипников условно включены в КПД передач для упрощения решения задачи)
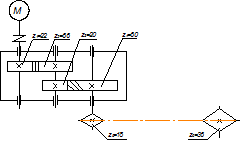
Рис.1 Схема привода
1.Дать характеристику привода.
Привод состоит из электродвигателя, цилиндрического двухступенчатого горизонтального редуктора (1 ступень – прямозубая передача, 2 ступень – косозубая передача) и цепной передачи.
2. Определить общий КПД привода.
η0 = η31 ∙ η32 ∙ ηЦ = 0,97 ∙ 0,98 ∙ 0,95 = 0,903
3.Определить общее передаточное отношение привода.
i0 = i31 ∙ i32 ∙ iЦ = 3 ∙ 3 ∙ 2 = 18
i31 = 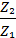 =
=  = 3 ; i32 =
= 3 ; i32 = 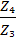 =
= 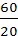 = 3 ;i ц =
= 3 ;i ц = 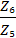 =
= 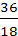 = 2
= 2
4. Определить угловые скорости всех валов привода.
ωдв = 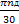 =
= 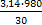 = 102,57
= 102,57 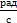
ω1 = ωдв = 102,57 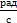 (соединение валов выполнено с помощью муфты, скорость не изменяется)
(соединение валов выполнено с помощью муфты, скорость не изменяется)
ω2 = 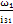 =
= 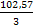 = 34,19
= 34,19 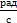
ω3 = 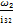 =
= 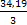 = 11,40
= 11,40 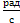
ω4 = 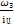 =
= 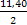 = 5,7
= 5,7 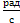
5. Определить мощности всех валов привода.
Рдв = 5 кВт
Р1= Рдв=5 кВт (КПД муфты не задано, поэтому мощность не изменяется)
Р2 = Р1∙η31= 5 ∙ 0,97 = 4,85 кВт
Р3 = Р2 ∙ η32 = 4,85 ∙ 0,98 = 4,75 кВт
Р4 = Р3 ∙ ηЦ = 4,75 ∙ 0,95 = 4,51 кВт
6. Определить вращающие моменты всех валов привода.
Тдв = 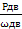 =
= 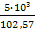 = 48,7 Нм
= 48,7 Нм
Т1 = 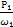 = Тдв = 48,7 Нм
= Тдв = 48,7 Нм
Т2 = 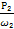 =
= 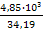 = 142 Нм
= 142 Нм
Т3 = 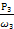 =
= 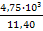 = 417 Нм
= 417 Нм
Т4 = 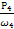 =
= 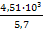 = 791 Нм
= 791 Нм
Вариант 2. Нет параметров одной из передач привода, но задана угловая скорость ωр.
Задача 16. Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 7,5 кВт, ωдв=150 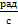 , ωр = 2,5
, ωр = 2,5 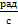 , ηр= 0,94, ηЗ1= 0,98, ηЗ2 = 0,98.
, ηр= 0,94, ηЗ1= 0,98, ηЗ2 = 0,98.
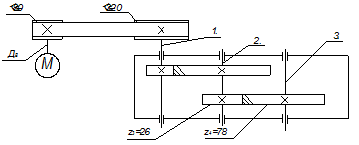
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из электродвигателя, ременной передачи и цилиндрического косозубого двухступенчатого горизонтального редуктора.
2. Определить общий КПД привода.
η0 = ηР ∙ η31 ∙ η32 = 0,94 ∙ 0,98 ∙ 0,98 = 0,903
3. Определить общее передаточное отношение привода.
Для данного варианта, когда нет параметров одной из передач, но задана угловая скорость на выходе из привода ωр, общее передаточное отношение привода определяется по формуле:
i0 = 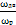 =
= 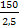 = 60 ,
= 60 ,
но для следующего пункта нужны передаточные отношения всех передач, поэтому:
ip = 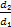 =
= 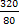 = 4
= 4
iЗ1 = 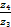 =
= 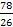 = 3
= 3
Так как i0 = ip ∙ iЗ1∙ iЗ2 , то iЗ1 = 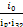 =
= 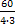 = 5
= 5
4. Определить угловые скорости всех валов привода.
ωдв=150 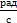
ω1 = 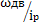 =
= 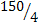 = 37,5
= 37,5 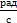
ω2 = 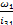 =
= 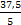 = 7,5
= 7,5 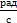
ω3 = 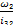 =
= 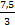 = 2,5
= 2,5 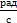
5. Определить мощности всех валов привода.
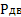 =7,5 кВт
=7,5 кВт
Р1 = Рдв∙ ηр = 7,5 ∙ 0,94 = 7,05 кВт
Р2 = Р1∙ ηЗ1 = 7,05 ∙0,98 = 6,91 кВт
Р3 = Р2∙ ηЗ2 = 6,91 ∙ 0,98 = 6,77 кВт
6. Определить вращающие моменты всех валов привода.
Тдв = 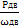 =
= 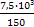 = 50 Нм
= 50 Нм
Т1 = 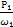 =
= 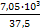 = 188 Нм
= 188 Нм
Т2 = 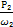 =
= 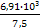 = 921 Нм
= 921 Нм
Т3 = 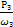 =
= 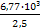 = 2710 Нм
= 2710 Нм
Задача 17. Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 5 кВт, ωдв = 150 рад\с, ηрем = 0,95, ηцил = 0,98, ηцеп = 0,92.
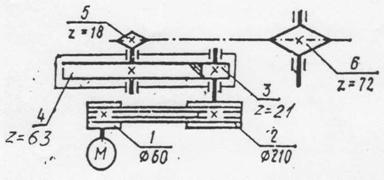 |
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
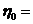
3. Определить общее передаточное отношение привода.
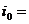
4. Определить угловые скорости всех валов привода.
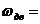
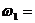
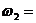
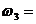
5.Определить мощности всех валов привода.
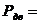

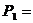
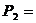
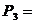
6. Определить вращающие моменты всех валов привода.
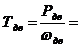
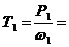
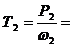
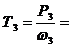
Задача 18. Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 10 кВт, ωдв = 102 рад\с , ηцеп = 0,92, ηз1 = 0,97, ηз2= 0,98.
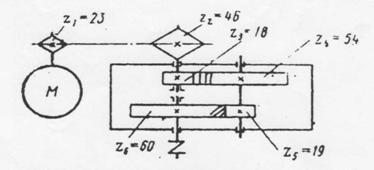 |
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
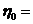
3. Определить общее передаточное отношение привода
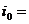
iцеп = iз1 = iз2 =
4. Определить угловые скорости всех валов привода.
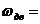
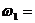
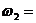
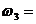
5.Определить мощности всех валов привода.
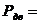

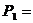
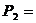
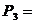
6. Определить вращающие моменты всех валов привода.
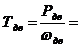
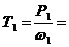
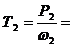
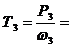
Задача 19. Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 4 кВт, nдв = 980 об\мин, 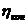 = 0,95 ,
= 0,95 , 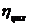 = 0,97,
= 0,97, 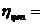 0,92.
0,92.
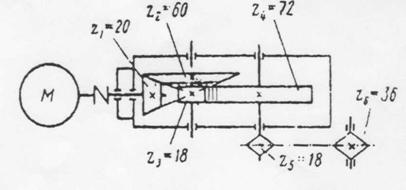 |
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
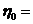
3. Определить общее передаточное отношение привода.
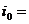
4. Определить угловые скорости всех валов привода.
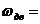
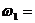
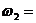
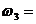
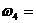
5.Определить мощности всех валов привода.
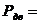
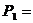
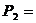
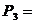
Р4 =
6. Определить вращающие моменты всех валов привода.
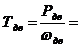
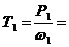
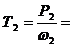
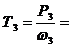
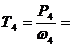
Задача 20. Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 12 кВт,
ωдв = 140 рад\с , η цил1= 0,98 , η цил2 = 0,98 , η кон = 0,92 , ωр = 4 рад\с.
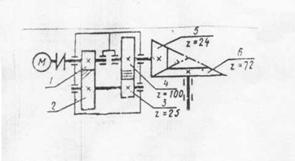
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
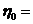
3. Определить общее передаточное отношение привода.
iо =
iцил1 = iцил2 = iкон =
4. Определить угловые скорости всех валов привода.
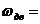
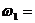
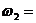
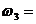
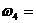
5.Определить мощности всех валов привода.
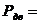

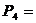
6. Определить вращающие моменты всех валов привода.
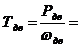
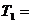
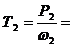
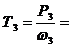
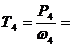
Задача 21 . Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 8 кВт, nдв = 1376 об\мин, η цил= 0,97, η кон = 0,96, η цеп = 0,92, ωр = 6 рад\с.
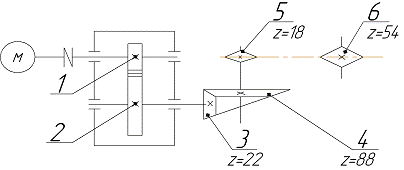
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
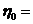
3. Определить общее передаточное отношение привода.
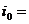
4. Определить угловые скорости всех валов привода.
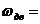
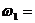
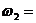
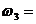
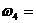
5. Определить мощности всех валов привода.
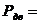

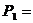
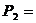
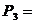
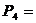
6. Определить вращающие моменты всех валов привода.
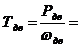
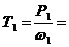
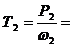
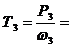
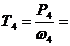
Задача 22 . Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 3 кВт, ωдв = 142 рад\с, η цеп = 0,95, η цил = 0,97, η кон = 0,96.
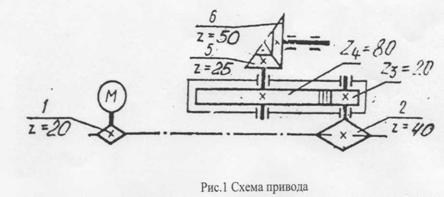 |
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
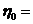
3. Определить общее передаточное отношение привода.
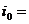
4. Определить угловые скорости всех валов привода.
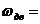
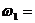
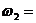
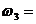
5. Определить мощности всех валов привода.
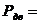
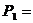
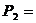
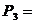
6. Определить вращающие моменты всех валов привода.
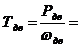
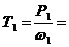
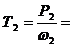
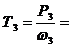
Задача 23 . Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 6 кВт, nдв = 975 об\мин, ηрем = 0,95, η кон = 0,96 , η цил = 0,97.
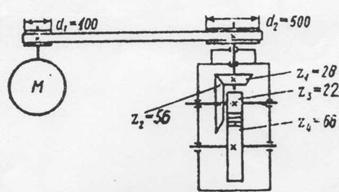 |
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
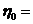
3. Определить общее передаточное отношение привода.
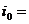
4. Определить угловые скорости всех валов привода.
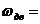
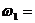
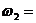
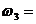
5. Определить мощности всех валов привода.
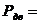

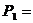
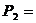
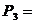
6. Определить вращающие моменты всех валов привода.
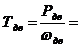
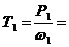
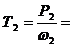
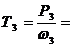
Часть 2. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Тема 2.1 Основные положения сопротивления материалов
1. Задачи сопротивления материалов – Сопротивление материалов это наука которая рассматривает деформируемое тела, и дает основы расчетов элементов конструкций на прочность, жесткость и устойчивость.
2. Гипотезы и допущения сопротивления материалов:
– связанные со свойствами материалов – сплошность и однородность, изотропность, идеальная упругость;
- связанные с деформациями – линейность и малость деформаций, гипотеза плоских сечений, принцип независимости действия сил.
МОДУЛЬ 3.
МОДУЛЬ 4.
Нормальные напряжения
Согласно гипотезе плоских сечений - поперечные сечения плоские и нормальные до деформации остаются плоскими и нормальными и после деформации. Это значит, что все точки поперечных сечений находятся в одинаковых условиях, т.е. нагружены равными внутренними силами, равнодействующая которых есть продольная сила. А значит и нормальные напряжения, возникающие в поперечных сечениях бруса при его осевом растяжении (сжатии) тоже распределены по всему поперечному сечению равномерно и определяются по формуле
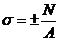 , МПа
, МПа
«+» соответствует растяжению, «-» - сжатию.
МОДУЛЬ 5.
МОДУЛЬ 6.
МОДУЛЬ 7.
Введение
Техническая механикасостоит из трех частей: 1. Теоретическая механика; 2. Сопротивление материалов; 3. Детали машин, и является теоретической базой для изучения специальных дисциплин.
Часть 1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Теоретическая механика – это наука, которая изучает законы движения тел и общие свойства движения. Состоит из трех разделов: статика; кинематика; динамика.
Допущенияпри изучении теоретической механики:
1. Материальная точка – это материальное тело, имеющее массу, размерами и формой которого в условиях данной задачи можно пренебречь.
2. Абсолютно твердое тело - это материальное тело, расстояния между любыми двумя точками которого остаются неизменными.
МОДУЛЬ 1.
Теоретическая механика. Статика. Системы сил, их условия и уравнения равновесия. Применение уравнений равновесия к решению задач.
Раздел 1. СТАТИКА
Статика - этораздел теоретической механики, который изучает правила сложения сил и условия равновесия тел под действием приложенных сил.
Тема 1.1 Основные понятия и аксиомы статики
1.Сила. Сила - мера механического взаимодействия тел. Единицы измерения: СИ – Н, (Ньютон). Сила тяжести G = mg = 1кг •9,81м/с2 = 9,81Н, (точность вычисления - три значащие цифры).
2.Система сил –это совокупность сил, действующих на тело.
3.Эквивалентные системы сил –это системы сил, оказывающие на тело одинаковое действие.
4. Равнодействующая сила– это сила, эквивалентная данной системе сил.
5. Уравновешивающая сила– это сила, уничтожающая действие данной системы сил.
6. Связи и реакции связей. Связь - это тело, препятствующее перемещению другого тела в пространстве. Сила, с которой связь действует на тело, называется реакцией связи.
Основные виды связей и их реакции (рис.1): а) Плоскость.Реакция N направлена перпендикулярно плоскости; б) Стержень (нить).Реакция F1 , F2 направлена вдоль стержня (нити); в) Шарнир неподвижный. Вертикальная Y и горизонтальная X реакции с плоскостью закрепления шарнира; г) Шарнир подвижный.Вертикальная Y реакция плоскости закрепления шарнира; д) Жесткая заделка.Вертикальная Y и горизонтальная X реакции и реактивный момент mр
а) б) в) г) д)
Рис.1 Основные виды связей и их реакции
Аксиомы статики - это основные положения, на которых основана теория равновесия.
Аксиома 1. Закон инерции или первый закон Ньютона. Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока другие силы не выведут его из этого состояния.
Аксиома 2. Условие равновесия двух сил.Для равновесия свободного твердого тела, находящегося под действием двух сил, необходимо и достаточно, чтобы эти силы были равны по модулю и действовали по одной прямой в противоположные стороны.
Аксиома 3. Принцип присоединения и исключения уравновешенных систем.Равновесие твердого тела не нарушится, если к нему приложить или от него отбросить систему уравновешенных сил.
Следствие(из А.3 и А.2).Перенос силы по линии ее действия.Механическое состояние твердого тела не нарушиться, если силу перенести по линии действия в любую точку.
Аксиома 4. Правило параллелограмма.Равнодействующая
двух сил, приложенных к телу в одной точке, равна по модулю и совпадает по направлению с диагональю параллелограмма, построенного на этих силах, как на сторонах. 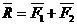 (рис.2)
(рис.2)
Рис.2 К аксиоме 4
Аксиома 5. Закон равенства действия и противодействия или третий закон Ньютона.Два тела действуют между собой с силами равными по модулю и противоположными по направлению.
Тема 1.2 Плоская система сходящихся сил (ПССС)
Это система сил, линии действия которых лежат в одной плоскости, и пересекаются в одной точке. Данная система сил эквивалентна равнодействующей силе.
При определении равнодействующей геометрическим способом последовательным сложением сил по правилу параллелограмма строится силовой многоугольник(треугольник), в котором составляющие силы системы расположены друг за другом, равнодействующая является замыкающей стороной (рис.1)
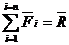 , Равнодействующая ПССС равна геометрической сумме составляющих сил.
, Равнодействующая ПССС равна геометрической сумме составляющих сил.
Рис.1 Силовой многоугольник
Проекцией силы на осьназывается отрезок, заключенный между двумя перпендикулярами, опущенными из начала и конца вектора силы на ось, и численно равный произведению модуля силы на косинус острого угла между линией действия силы и осью (рис. 2)
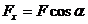
Рис.2 К проекции силы на ось
Правило знаков проекции:
«+» , если направление силы совпадает с положительным направлением оси;
« - » , если направление силы не совпадает с положительным направлением оси.
Частные случ
