Двухполюсные сети. Потоки в сетях

Сеть – это граф, некоторые вершины которого выделены; они называется полюсамисети. Вершины, отличные от полюсов, называются внутренними вершинамисети. Ребра, инцидентные хотя бы одному полюсу, называются полюсными ребрами; остальные ребра называются внутренними.

(k, l)-полюсникомназывается сеть с (k + l) полюсами, разбитыми на два класса: k входных и
l выходных полюсов. (1, 1)-полюсник называется также двухполюсной сетью. В этом параграфе мы будем рассматривать, главным образом, двухполюсные сети без петель и без изолированных внутренних вершин (кратные ребра допускаются). Они будут называться просто сетями. Будем также называть цепью(без указания концов) элементарную цепь между полюсами сети - в других случаях будем обязательно указывать концы цепи или называть ее цепочкой. Обозначим входной и выходной полюсы сети S символами α_Sи β_S. Полюсные ребра образуют входную и выходную звезды Z_α и Z_β, пересечение которых состоит из сквозных ребер (оно может быть пустым), инцидентных обоим полюсам. Однореберная сеть состоит из одного ребра; его концы являются полюсами сети.

Пусть А и В - две цепи сети S, не имеющие общих внутренних вершин, α и β - внутренние вершины этих цепей, С - элементарная цепочка [α, β], не пересекающаяся с А и В нигде, кроме своих концов (рис. 2.19). Тогда существуют две цепи, проходящие через цепочку С в разных направлениях: [α_SА₁ α С β В₂ β_S] и [α_SВ₁ β С α А₂ β_S]. Подграф, образованный парой таких цепей А и В и связывающей их цепочкой С, называется мостиком.

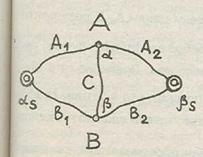
Рис. 2.19

Рассмотрим две операции над сетями. Пусть S₁- сеть с полюсами α₁и β₁, S₂- сеть с полюсами α₂и β₂, причем S₁и S₂не имеют общих элементов. Сеть S₁• S₂с полюсами α₁и β₂, полученная склеиванием вершин β₁и α₂, называется последовательным соединением сетей S₁и S₂
(рис. 2.20, а); сеть S₁Ú S₂с полюсами α₁и β₁, полученная склеиванием полюсов α₁с α₂и β₁с β₂, называется параллельным соединениемсетей S₁и S₂(рис. 2.20, б). Аналогично
определяются последовательное и параллельное соединения большего числа сетей:
S₁• S₂•...• S_n и S₁Ú S₂Ú ... Ú S_n.

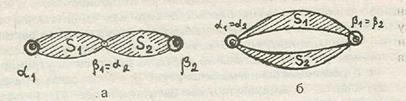
Рис. 2.20

Сеть, полученная из однореберных сетей в результате конечного числа применений операции параллельного и последовательного соединения, называется параллельно-последовательной сетью. Другими словами, класс параллельно-последовательных сетей (сокращенно П-сетей) определяется индуктивно:

(1) однореберная сеть есть П-сеть;

(2) если S₁и S₂ - П-сети, то S₁• S₂и S₁Ú S₂ - тоже П-сети.

Это пример задания множества порождающей процедурой. Характеристическое свойство
П-сетей: они не содержат мостиков.

Добавим к сети S дополнительное, источниковое ребро, связывающее полюсы (иногда, например, в случае ориентированных сетей бывает удобным ориентировать это ребро от выхода к входу сети). Полученную расширенную сеть обозначим через . Заметим, что добавление источникового ребра к любой цепи А превращает ее в элементарный цикл .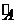

Нетрудно показать, что в произвольной сети сумма по модулю 2 нечетногочисла цепей Аiсодержит цепь. В самом деле, сложим по модулю 2 циклы 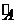_i, соответствующие данным цепям Аi. В результате получим четный граф å 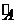_i. Источниковое ребро входит в эту сумму, так как оно участвует в сложении нечетное число раз. Очевидно, что оно является циклическим ребром в å 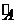_i (напомним, что в четном графе все ребра циклические). Содержащий его цикл после удаления самого источникового ребра есть искомая цепь.

Пусть S - произвольная частично ориентированная сеть, каждому ребру е которой приписано неотрицательное число с(e) - пропускная способность (пример на рис. 2.21). Потоком в сети Sназывается пара (f, w), где w - некоторая ориентация всех неориентированных ребер сети, а f(e) - заданная на множестве всех ребер функция с неотрицательными значениями, не превосходящая пропускных способностей, и такая, что в каждой внутренней вершине выполнен закон Кирхгофа, согласно которому сумма значений потока по ребрам, входящим в вершину, равна сумме значений потока по ребрам, исходящим из вершины. Другими словами, для f(e) выполнены условия:

(1) 0 ≤ f(e) ≤ c(e) для всех ребер сети;

(2) R(α) = 0 для всех внутренних вершин α,

где R(α) = 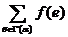– 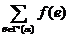, а Г(α) (соответственно, Г¢(α)) – множество всех ребер, исходящих из α (соответственно, входящих в α) при ориентации w.

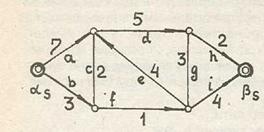
Рис. 2.21

Поскольку сумма значений R(α) по всем вершинам сети, включая полюсы, равна 0 (каждое ребро является исходящим для одной вершины и входящим для другой), то R(α_s) = -R(β_s). Значение R = R(α_s) называется величиной потока. Между прочим, сходные рассуждения показывают, что если сеть допускает поток ненулевой величины, то полюсы сети находятся в одной компоненте связности. Если сеть изображает какую-либо проводящую систему (сеть дорог, трубопровод и т.п.), то R определяет величину потока, входящего в одном полюсе и выходящего из другого, т.е. проходящего через сеть. Если на ориентированном от β_s к α_s источниковом ребре положить f = R (допуская, что для этого ребра f может быть меньше 0), то закон Кирхгофа будет выполняться для всех вершин сети, а R будет определять величину циркуляции через сеть.

Поставим задачу определить максимальную величину потока Rmaxчерез сеть S при заданных значениях пропускных способностей. Ответ может быть получен в терминах сечений сети.

Сечением в сетиназывается множество ребер, при удалении которого сеть становится несвязной, причем полюсы попадают в разные компоненты связности. Ясно, что каждая цепь
(а тем более каждый путь из α_s в β_s) проходит хотя бы через одно ребро сечения. В сети на
рис. 2.21 примерами сечений являются {d, e, f}, {b, c, e, g, h}, {d, g, h, i}. Сечение будем называть простым, если при удалении любого его ребра оно перестает быть сечением. Так, {d, e, f} и
{b, c, e, g, h} являются простыми сечениями, в то время как {d, g, h, i} не является таковым: можно удалить ребро h или ребро i. Очевидно, что для каждого ребра простого сечения можно указать цепь, которая проходит через это ребро, но не проходит через другие ребра данного сечения: иначе это ребро было бы излишним.

Если в связной сети удаляется простое сечение, то сеть распадается ровно на две части:
левую часть, содержащую α_s, и правую часть, содержащую β_s. Каждое ребро простого
сечения связывает вершины из разных частей. Будем называть ребро сечения прямым, если оно в сети не ориентировано или ориентировано слева направо, и обратным- в противном случае. Будет ли ориентированное ребро прямым или обратным, вообще говоря, зависит от выбора сечения. Так, в примере на рис. 2.21 ребро е в сечениях {d, e, f} и {b, c, e, g, h} - обратное, а в сечении {а, c, e, g, i} - прямое.

Каждому простому сечению W припишем пропускную способность c(W), равную
сумме пропускных способностей всех его прямых ребер. В примере на рис. 2.21 сечение {d, e, f} имеет пропускную способность 5 + 1 = 6, а сечение {b, c, e, g, h} - пропускную способность
3 + 2 + 3 + 2 = 10. Если сеть несвязна и ее полюсы находятся в разных компонентах связности, то естественно считать (единственным) простым сечением пустое множество, а его пропускную способность нулевой.

Теорема Форда-Фалкерсона о максимальном потоке:максимальная величина потока Rmaxчерез сеть S равна минимальной из пропускных способностей сminее простых сечений.

Неравенство Rmax≤ сminможно считать достаточно очевидным из физических соображений, и в его справедливости нетрудно убедиться, просуммировав величину R(α) по всем вершинам α левой компоненты произвольного сечения W. Эта сумма, с одной стороны, равна R(α_s), а с другой стороны, она равна алгебраической сумме величин потоков, идущих через сечение слева направо (потоки по ребрам, идущим из левой компоненты в правую суммируются со знаком плюс, а по ребрам, идущим в обратном направлении, - со знаком минус). Поскольку f(e)≤ c(e), отсюда следует, что R ≤ c(W). Ясно также, что равенство R = c(W) может достигаться только, если все прямые ребра сечения W ориентированы слева направо (при ориентации w) и для них f(e) = c(e), а для всех обратных ребер f(e) = 0.

Несколько сложнее доказывается, что в сети S можно создать поток величины, равной сmin.

Разработан ряд конкретных алгоритмов построения максимального потока, основанных на этой теореме.

Теорема Форда-Фалкерсона допускает обобщение на случай, когда пропускные способности приписаны не только ребрам, но и внутренним вершинам сети, и поток считается допустимым, если для любой внутренней вершины α величина 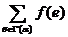(так же как и величина 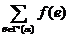) не превосходит пропускной способности вершины α. Теорема распространяется и на (k, l)-полюсную сеть. В обоих случаях величина максимального потока от входов к выходам сети равна минимальной пропускной способности множества элементов сети, блокирующего все цепи.

Наряду с определением максимальных потоков в тех или иных проводящих системах теорема Форда-Фалкерсона позволяет решать и некоторые чисто комбинаторные проблемы. Одна из них носит название задачи о назначениях. Пусть имеется N претендентов {ai} на N вакантных должностей {bj}. Возможно ли назначение всех N кандидатов, если каждый из них способен занять одну из некоторого подходящего ему подмножества Вiэтих должностей? Очевидным является следующее необходимое условие такой возможности: для любой группы k ≤ N претендентов объединение соответствующих им множеств Вiдолжно содержать не меньше k должностей - иначе им не хватит мест (вспомните комбинаторный принцип Дирихле).

Ситуация может быть представлена двудольным графом (рис. 2.22), где V₁= {ai}, V₂= {bj} и (ai, bj) - дуга графа, если кандидат aiспособен занять должность bj. Если ввести
две дополнительные вершины - полюсы s и t, дополнительные дуги (s, ai) и (bj, t), установить подходящим образом пропускные способности вершин и ребер, то с помощью теоремы Форда-Фалкерсона можно показать, что приведенное условие является также достаточным.

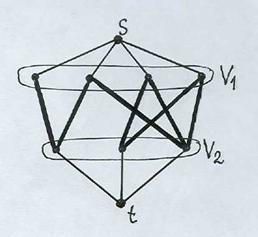
Рис. 2.22