Нахождение точек пересечения функции с координатными осями
Найдём пересечение с осью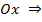 
y = 0
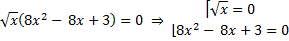
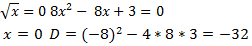
Так как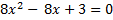 
имеет только комплексные корни, получаем
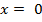
Следовательно, функция пересекает ось Oxв точке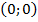 
Найдём пересечение с осью 
x = 0
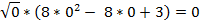
Следовательно, функция пересекает ось Oyв точке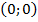
Нахождение промежутков знака функции
Рассмотрим промежуток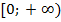 
При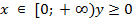 
Исследование поведения функции на границах области определения.
При приближении к 0±
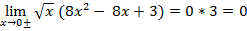
При приближении к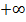 
Нахождение промежутков возрастания и убывания функции
Промежутки возрастания и убывания являются решениями неравенств
и 
соответственно.
=
Находим нули числителя:
Находим нули знаменателя:
, x 
Наносим эти точки на числовую ось и определяем знак производной внутри каждого полученного промежутка.
0 
+ 
Следовательно, функция 
возрастает
на промежутке(0; 
] 
[ 
; + 
и убывает на промежутке[ ; ].
Нахождение промежутков выпуклости и вогнутости функции и точек перегиба.
Промежутки вогнутости и выпуклости функции находятся при решении неравенств
и 
соответственно.
Находим нули числителя:
Находим нули знаменателя:
Наносим эти точки на числовую ось и определяем знак двойной производной внутри каждого полученного промежутка.
+
Следовательно, функция 
выпукла на промежутке
(0; 
]и вогнута на промежутке [ ; +∞), при этом точка, соответствующая
x= , является точкой перегиба функции.
Нахождение асимптот функции
У функции отсутствуют вертикальные асимптоты.
Найдем наклонную асимптоту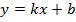 
.
…
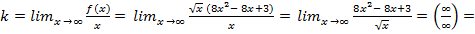Воспользуемся правилом Лопиталя и найдем производные числителя и знаменателя.
.
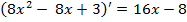
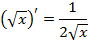
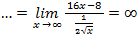Поскольку коэффициент k равен бесконечности, наклонных асимптот у данной функции не существует.
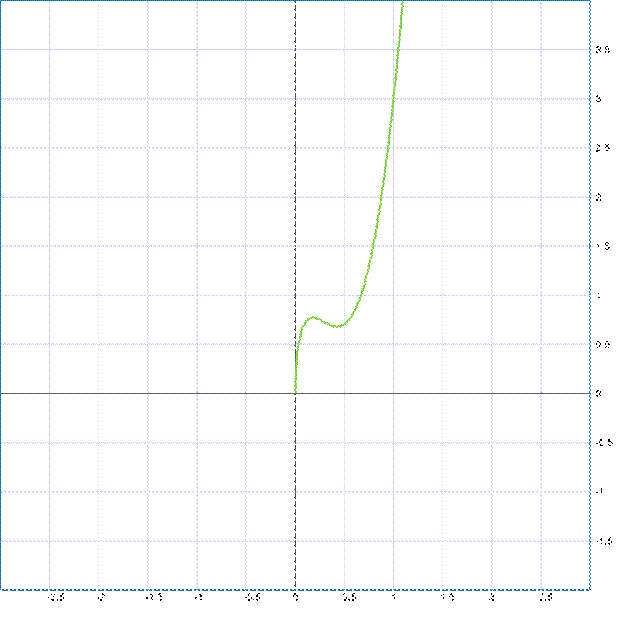
Построение графика функции.
Вручную:
С помощью компьютера:
Описание второй задачи
Фигура, ограниченная линиями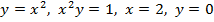 
вращается вокруг оси Ox. Найти объём тела вращения.Проверить ответ на компьютере.
Анализ функций и построение фигуры, образующей тело вращения
Для удобства функцию 
В первую очередь убедимся в том, что представленные функции определены и непрерывны на ℝ. Это следует из того, что любая степенная функция с натуральным показателем определена на всей числовой оси, а любая элементарная функция непрерывна на области своего определения. Затем построим графики и найдём точки пересечения функций.
, 
Таким образом, для поиска объема данного тела вращения нам потребуются найти интеграл с границами интегрирования 
и 
.
Нахождение объёма тела вращения
Так как фигура вращается вокруг оси Ox, для упрощения дальнейших вычислений перепишем кривые, ограничивающие фигуру, в виде 
Находим объём тела вращения как разницу объёмов тел вращения фигур, первая из которых ограничена графиком и осью Ox, а вторая графиком 
и осью Oxс помощью формулы
,
Проверка результатов расчётов на компьютере
Для проверки использовался сайтWolframAlpha.com