Отличительные черты задач устойчивости стержней, пластин и оболочек
Отличительные черты задач устойчивости стержней, пластин и оболочек

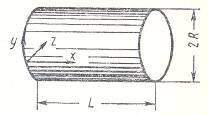
Основные уравнения для круговых цилиндрических оболочек
Рассмотрим упрощенный вариант линейной теории, когда выпучивание сопровождается появлением мелких волн, размеры которых хотя бы в одном направлении малы по сравнению с размерами оболочки. В результате оболочку в пределах выпучины можно рассматривать как пологую. Например, в осесимметричном случае число выпучин вдоль окружности должно быть n≥4. Это условие выполняется для оболочек средней длины. По Даревскому В.М:
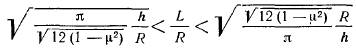 или
или
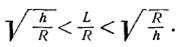
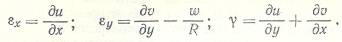 - деформации
- деформации
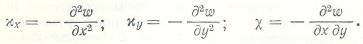 - кривизны
- кривизны
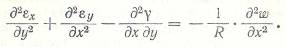 - уравнение совместности деформаций
- уравнение совместности деформаций
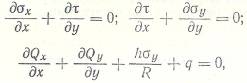 - уравнения равновесия на оси х,y и нормаль
- уравнения равновесия на оси х,y и нормаль
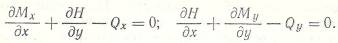 - уравнения моментов
- уравнения моментов
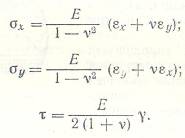 - обобщенный закон Гука
- обобщенный закон Гука
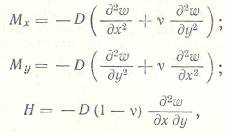 где
где 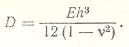
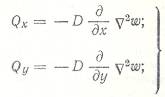 где
где 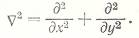
Подставим перерезывающие силы в 3-ье уравнение равновесия:
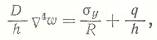 где
где 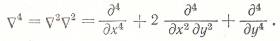
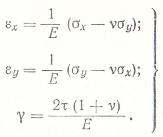
Подставим деформации в уравнение совместности:
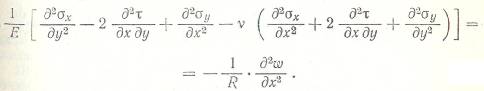
Введем функцию напряжений срединной поверхности Ф:
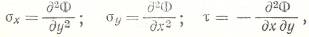
В результате получим:
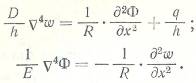 (*)
(*)
Подставим вместо qфиктивную поперечную нагрузкуq0, равную сумме дополнительных проекций основных усилий px, py иs на направление нормали (усилие px – действует вдоль оси х, усилие py – вдоль касательной к оси y иусилие s - касательные)
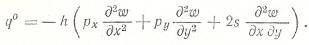
В результате получим:
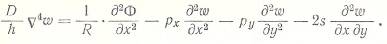
Применим оператор 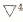 , а к (*) оператор
, а к (*) оператор 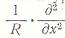 , в результате получим одно уравнение:
, в результате получим одно уравнение:
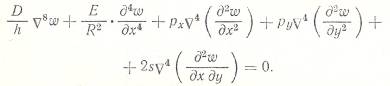
Вариант уравнений линейной теории оболочек для случая слабовыраженного волнообразования по длине оболочки. В этом случае срединную поверхность считают нерастяжимой в дуговом направлении 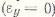 ; отсутствуют сдвиги в срединной поверхности
; отсутствуют сдвиги в срединной поверхности  . Равны нулю также
. Равны нулю также 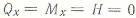 . Отличны от нуля лишь
. Отличны от нуля лишь 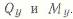 . В результате получим:
. В результате получим:
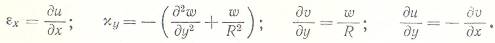
Отсюда 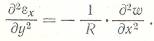
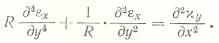 - уравнение совместности деформаций
- уравнение совместности деформаций
Уравнения равновесия примут вид
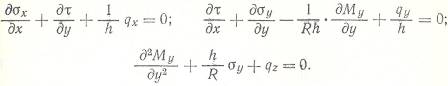
Где 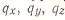 - внешняя нагрузка вдоль оси х, касательной к линии y и к оси z
- внешняя нагрузка вдоль оси х, касательной к линии y и к оси z
Объединяя их получим
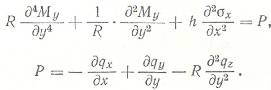
Закон Гука примет вид
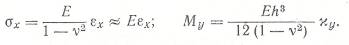
Вводя переменные 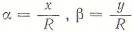 и пользуясь оператором
и пользуясь оператором 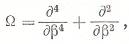 получим
получим
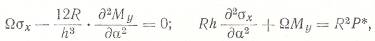 где
где 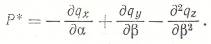
Исключая 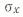 и пользуясь уравнением
и пользуясь уравнением 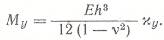 после исключения оператора
после исключения оператора 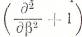 получим:
получим:
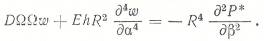
Этим уравнением пользуются для исследования оболочек средней и особенно большой длины в случае слабовыраженного волнообразования по длине оболочки. Линейная теория дает возможность исследовать устойчивость оболочки в малом. Полное решение задачи, включающее исследование потери устойчивости в большом, может быть дано с позиций нелинейной теории.
Оболочка большого прогиба.
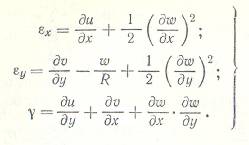
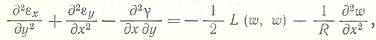 - уравнение совместности деформаций, где
- уравнение совместности деформаций, где 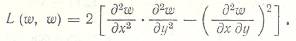
Изменение кривизн, кручение, выражения для поперечных сил, закон Гука - прежние.
Третье уравнение равновесия примет вид:
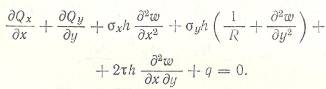
В результате получим:

Где 
Оболочка с начальными прогибами 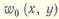
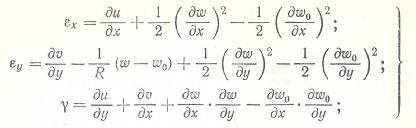 где
где 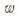 - полный прогиб
- полный прогиб
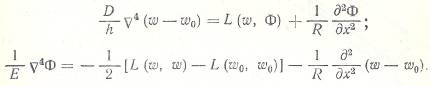
Граничные условия:А) шарнирное опирание 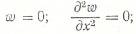
Б) жесткая заделка (защемление) 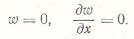
В) края оболочки свободно смещаются вдоль образующей и по дуге 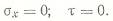
Г) несмещающиеся кромки 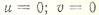
Нелинейная задача


  Второй – отражает несимметричность прогиба относительно срединной поверхности с преимущественным направлением к центру кривизны; третий – соответствует радиальным перемещениям точек, принадлежащих торцевым сечениям х=0,L. Второй – отражает несимметричность прогиба относительно срединной поверхности с преимущественным направлением к центру кривизны; третий – соответствует радиальным перемещениям точек, принадлежащих торцевым сечениям х=0,L. |
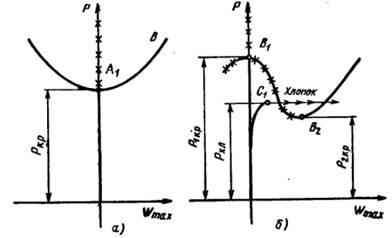
Случай внешнего давления
 Из уравнения равновесия получаем Из уравнения равновесия получаем      Обозначим Обозначим   Примем Примем   Минимизируяqпо n, получим: Минимизируяqпо n, получим:   Окружное напряжение равно Окружное напряжение равно   |
   |
Устойчивость при изгибе
  Распределение нормальных напряжений в поперечных сечениях Распределение нормальных напряжений в поперечных сечениях  Деформации в срединной поверхности равны Деформации в срединной поверхности равны    После подстановки приравниваем коэффициенты при однородных членах, тогда приходим к трехчленным уравнениям относительно fn: После подстановки приравниваем коэффициенты при однородных членах, тогда приходим к трехчленным уравнениям относительно fn:  Здесь учитывалось, что Здесь учитывалось, что  Ограничившись определенным числом параметров fn и вычислив определитель, то можно определить критическую нагрузку р0. Ограничившись определенным числом параметров fn и вычислив определитель, то можно определить критическую нагрузку р0.  |
Коническая оболочка
Осевое сжатие конической оболочки  Считаем, что при потере устойчивости образуется большое число волн, длина которых невелика, поэтому s можно считать постоянной Считаем, что при потере устойчивости образуется большое число волн, длина которых невелика, поэтому s можно считать постоянной  Решение ищем в виде (l1 – расстояние вдоль образующей от вершины до большего основания, лямбда – длина волны) Решение ищем в виде (l1 – расстояние вдоль образующей от вершины до большего основания, лямбда – длина волны)   Приравниваем нулю определитель системы и учитывая обозначение Приравниваем нулю определитель системы и учитывая обозначение  получим получим  Минимизируем N по квадрату β, получим Минимизируем N по квадрату β, получим    где R0 – радиус кривизны срединной поверхности у большего основания где R0 – радиус кривизны срединной поверхности у большего основания  Внешнее давление конической оболочки Внешнее давление конической оболочки    Внешнее давление усеченной конической оболочки Внешнее давление усеченной конической оболочки    (гр. условия – большее основание шарнирное опирание, меньшее – жесткая заделка) (гр. условия – большее основание шарнирное опирание, меньшее – жесткая заделка) |
Сферическая оболочка
   |   Сжимающие усилия и напряжения примем Сжимающие усилия и напряжения примем     Примем, что Примем, что  где лямбда – неопределенный параметр (Власов) где лямбда – неопределенный параметр (Власов)  Минимизируя сигма по квадрату лямбда Минимизируя сигма по квадрату лямбда    |
Эллипсоидальные оболочки
 Вытянутая оболочка Вытянутая оболочка  |   Сплющенная оболочка под внутренним давлением Сплющенная оболочка под внутренним давлением   |
Пологие оболочки
  |  Уравнения для оболочки, имеющей начальные отклонения от идеальной формы Уравнения для оболочки, имеющей начальные отклонения от идеальной формы  Уравнения для пластинки с начальной погибью ( Уравнения для пластинки с начальной погибью (  ) )   Оба подхода эквивалентны Оба подхода эквивалентны |
 | Панель прямоугольная в плане   Аналогично для y=0 и b Аналогично для y=0 и b     Введем безразмерные параметры Введем безразмерные параметры   Для квадратной панели Для квадратной панели     |
Сферическая панель





Отличительные черты задач устойчивости стержней, пластин и оболочек







