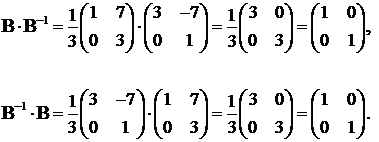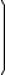Понятие матрицы. Виды Матриц.

Определение.Матрицей размера m 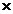n называется прямоугольная таблица чисел, содержащая mстрок и n столбцов.

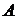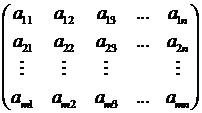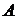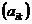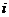= или = , =1,2,…, 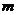, 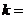1,2,…, .

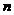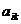– элемент матрицы, стоящий на пересечении 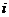-й строки и 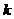-го столбца.

Определение. Если 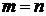, то матрица называется квадратнойn-го порядка, в противном случае – прямоугольной.

Элементы 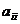, 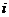= 1, 2, …, n квадратной матрицыА образуют ее главную диагональ.

Матрица размера 1хn называется матрицей-строкой, а матрица размера 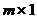– матрицей-столбцом.

Определение. Две матрицы называются равными, если они имеют одинаковый размер и равны их элементы, стоящие на одинаковых местах.

Определение. Квадратная матрица называется диагональной, если равны нулю все ее элементы, расположенные вне главной диагонали, то есть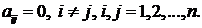

На главной диагонали могут быть любые числа. Если все они равны 1, то диагональная матрица называется единичной и обозначается буквой .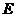

Определение. Квадратная матрица называется треугольной, если все ее элементы снизу (сверху) от главной диагонали равны нулю.

Действия над матрицами

Сложение и вычитание матриц

Складывать и вычитать можно матрицы одного размера в результате получается матрица того же размера.

Определение.Сложение матриц (сумма матриц) A + B есть операция вычисления матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:

сij = aij + bij

Определение.Вычитание матриц (разность матриц) A - B есть операция вычисления матрицы C, все элементы которой равны попарной разности всех соответствующих элементов матриц A и B, то есть каждый элемент матрицыC равен:

с_ij = a_ij - b_ij

Примеры задач на сложение и вычитание матриц

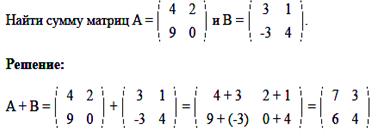
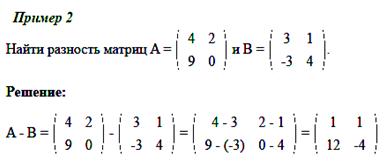
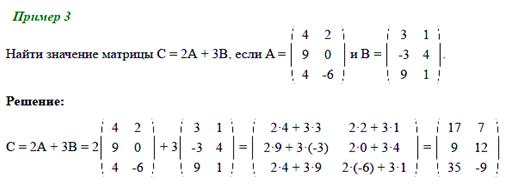
Умножение матриц

Определение.Результатомумножения матрицA_m×nиB_n×kбудет матрицаC_m×kтакая, что элементматрицыC, стоящий вi-той строке иj-том столбце (c_ij), равен сумме произведений элементов i-той строки матрицыAна соответствующие элементыj-того столбца матрицыB:

c_ij = a_i1 · b_1j + a_i2 · b_2j + ... + a_in · b_nj

Замечание.Две матрицы можно перемножить между собой тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.

Свойства умножения матриц

• (A · B) · C= A · (B · C) - произведение матриц ассоциативно;
• (z · A) · B=z · (A · B), гдеz - число;
• A · (B + C) = A · B + A · C - произведение матриц дистрибутивно;
• E_n· A_nm= A_nm· E_m= A_nm- умножение наединичную матрицу;
• A · B ≠ B · A - в общем случае произведение матриц не коммутативно.
• Произведением двух матриц есть матрица, у которой столько строк, сколько их у левого сомножителя, и столько столбцов, сколько их у правого сомножителя.

Примеры на умножение матриц

Пример 1.

Найти матрицу C равную произведению матриц A =				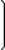	и B =					.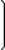
		-3

Решение:

С = A · B =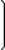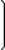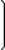

·

=

-3

Элементы матрицы C вычисляются следующим образом:

c₁₁ = a₁₁·b₁₁ + a₁₂·b₂₁ = 4·3 + 2·(-3) = 12 - 6 = 6

c₁₂ = a₁₁·b₁₂ + a₁₂·b₂₂ = 4·1 + 2·4 = 4 + 8 = 12

c₂₁ = a₂₁·b₁₁ + a₂₂·b₂₁ = 9·3 + 0·(-3) = 27 + 0 = 27

c₂₂ = a₂₁·b₁₂ + a₂₂·b₂₂ = 9·1 + 0·4 = 9 + 0 = 9

Пример 2.

Найти матрицу C равную произведению матриц A =

-3 -1

и B =

-1 -3

.

Решение:

C = A · B =

-3 -1

·

-1 -3

=

-2 -15 -18 -4

Элементы матрицы C вычисляются следующим образом:

c11 = a11·b11 + a12·b21 = 2·5 + 1·(-3) = 10 - 3 = 7

c12 = a11·b12 + a12·b22 = 2·(-1) + 1·0 = -2 + 0 = -2

c13 = a11·b13 + a12·b23 = 2·6 + 1·7 = 12 + 7 = 19

c21 = a21·b11 + a22·b21 = (-3)·5 + 0·(-3) = -15 + 0 = -15

c22 = a21·b12 + a22·b22 = (-3)·(-1) + 0·0 = 3 + 0 = 3

c23 = a21·b13 + a22·b23 = (-3)·6 + 0·7 = -18 + 0 = -18

c31 = a31·b11 + a32·b21 = 4·5 + (-1)·(-3) = 20 + 3 = 23

c32 = a31·b12 + a32·b22 = (4)·(-1) + (-1)·0 = -4 + 0 = -4

c33 = a31·b13 + a32·b23 = 4·6 + (-1)·7 = 24 - 7 = 17

Определение.Транспонирование матрицы - это операция над матрицей, при которой ее строки и столбцы меняются местами:

(a_ij) ^T= a_ji

Определение. Обратная матрица A⁻¹ - матрица, произведение которой на исходную матрицу A равно единичной матрице E:

A·A^-1 = A^-1·A = E

Обратная матрица для матрицы 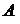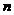- го порядка имеет вид:

.

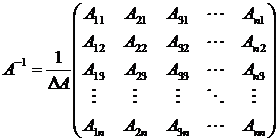Замечание.Обратная матрица существует только для квадратных матриц определитель которых не равен нулю.

Теорема. Всякая невырожденная матрица имеет обратную, причем одну.

Определение. Квадратная матрица 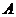называется невырожденной, если 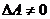. Если 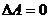, то 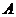называется вырожденной.

Пример. 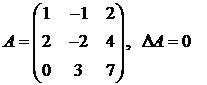по свойству 6 определителей, то есть 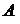– вырожденная.

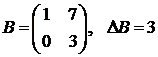, значит, 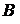– невырожденная.

Пример. Найти матрицу, обратную для .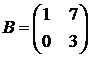

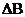=3 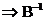существует.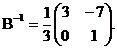

Проверка: