Операции над нечеткими подмножествами

Для классических множеств вводятся операции:

· пересечение множеств – операция над множествами А и В, результатом которой является множество С = А Ç В, которое содержит только те элементы, которые принадлежат и множеству A и множеству B;

· объединение множеств - операция над множествами А и В, результатом которой является множество С = А È В, которое содержит те элементы, которые принадлежат множеству A или множеству B или обоим множествам;

· отрицание множеств - операция над множеством А, результатом которой является множество С = Ø А, которое содержит все элементы, которые принадлежат универсальному множеству, но не принадлежат множеству A.

Заде предложил набор аналогичных операций над нечеткими множествами через операции с функциями принадлежности этих множеств.

Так, если множество А задано функцией m_А(u), а множество В задано функцией m_В(u), то результатом операций является множество Сс функцией принадлежности m_С(u), причем:

· если С = А Ç В, то m_С(u) = min(m_А(u), m_В(u)); (2.2)

· если С = А È В, то m_С(u) = max(m_А(u), m_В(u)); (2.3)

· еслиС = Ø А,то m_С(u) = 1-m_А(u). (2.4)

Нечеткие последовательности, нечеткие прямоугольные матрицы, нечеткие функции и операции над ними

Нечеткая последовательность – это пронумерованное счетное множество нечетких чисел.

Нечеткая прямоугольная матрица – это дважды индексированное конечное множество нечетких чисел, причем первый индекс пробегает M строк, а второй - N столбцов. При этом, как и в случае матриц действительных чисел, операции над нечеткими прямоугольными матрицами сводятся к операциям над нечеткими компонентами этих матриц. Например,

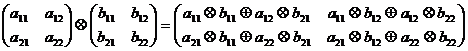, (2.12)

где все операции над нечеткими числами производятся так, как они введены параграфом выше.

Нечеткая функция – это взаимно однозначное соответствие двух полей нечетких чисел.

Например [2.3], прогноз продаж компании (нарастающим итогом) задан тремя функциями вещественной переменной: f₁(T) – оптимистичный прогноз, f₂(T) – пессимистичный прогноз, f₃(T) – среднеожидаемые значения продаж, где Т – время прогноза. Тогда лингвистическая переменная «Прогноз продаж в момент Т»есть треугольное число ( f₁(T), f₂(T), f₃(T) ), а все прогнозное поле есть треугольная нечеткая функция (рис. 2.5), имеющая вид криволинейной полосы.

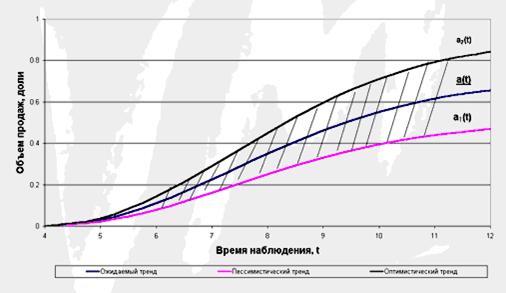
Рис. 2.5. Треугольная нечеткая функция. Источник: [2.3]

Рассмотрим ряд операций над треугольными нечеткими функциями(утверждения приводятся без доказательства):

· сложение: сумма (разность) треугольных функций есть треугольная функция;

· умножение на число переводит треугольную функцию в треугольную функцию;

· дифференцирование (интегрирование)треугольной нечеткой функции проводится по правилам вещественного дифференцирования (интегрирования):

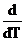( f₁(T), f₂(T), f₃(T) ) = ( 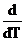f₁(T), 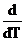f₂(T), 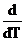f₃(T) ), (2.13)

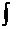( f₁(T), f₂(T), f₃(T) ) dT = ( 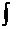f₁(T)dT, 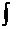f₂(T) dT, 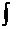f₃(T) dT ), (2.14)

· функция, зависящая от нечеткого параметра, является нечеткой.