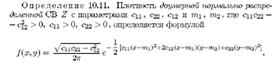Функция распределения и ее свойства.
Значение функции распределения F(x1,y1) равно вероятности попадания двумерной СВ (X,Y) в бесконечный квадрант D11 с вершиной в точке (x1, y1)
1) F(x,y) определена для всех (x,y) О R2, так как вероятность P{X ≤ x, Y ≤ y} определена для всех x,y О R1.
2) 0 ≤ F(x,y) ≤ 1 для всех x,y О R1. По аксиоме A1 и свойству 5)P для любого события выполняется 0 ≤ P(A) ≤ 1 , поэтому по определению F(x,y) О [0,1].
3) F(-∞,y) = F(x,-∞) = F(-∞,-∞) = 0 для всех x,y О R1. Например, рассматривая
| Bn | Δ = | {ω : Y(ω) ≤ -n}, где n = 1, 2, ... , |
можно по аналогии с доказательством свойства 3)F(x) установить, что
| F(-∞,y) ≤ | l i m n→∞ | P(Bn) = P( Ж ) = 0. |
4) FY(y) = F(+∞,y), FX(x) = F(x,+∞) для всех x,y О R1, где FX(y) и FY(x) - функции распределения СВ X и Y соответственно. Это свойство можно установить, следуя доказательству свойства 3)F(x), т.к. {ω : X(ω) ≤ +∞} = {ω : Y(ω) ≤ +∞} = Ω.
5) F(+∞,+∞) = 1. В силу свойства 4)F(x,y) имеем
| F(+∞,+∞) = FX(+∞) | 3)F(x) = | 1. |
6) F(x,y) - монотонно неубывающая по каждому из аргументов. Т.к. для Δx > 0 имеем
| F(x+Δx,y) | Δ = | P{X ≤ x+Δx, Y ≤ y} | A3 = |
= P{X ≤ x,Y ≤ y} + P{x < X ≤ x + Δx, Y ≤ y},
так как рассматриваемые события несовместны. По аксиоме A1 имеем F(x + Δx,y) ≥ F(x,y). Монотонность F(x,y) по y доказывается аналогично.
7) Если F(x,y) непрерывна по x и y, то вероятность попадания СВ Z в прямоугольник D = {x1 ≤ x ≤ x2, y1 ≤ y ≤ y2} равна
| P(D) | Δ = | F(x2,y2) + F(x1,y1) - F(x1,y2) - F(x2,y1), |
где F(xi,yj), (i,j = 1,2) - вероятности попадания СВ Z в квадранты Dij с соответствующими вершинами (xi,yj), i,j = 1,2
Условная плотность распределения и ее свойства.
Условной плотностью распределения (вероятности) непрерывной СВ X при условии, что непрерывная СВ Y с плотностью fY(y) ≠ 0 приняла значение y, называется функция
| f( x | y) = | f(x, y) fY(y) | , x О R1 . |
1) fx(x|y) ≥ 0, так как плотности f(x,y) ≥ 0, fY(y) ≥ 0.
| 2) | Fx(x|y) | Δ = | x ∫ -∞ | fX(x|y) dx, |
если плотности f(x,y), fY(y) непрерывны. В этом можно убедиться, сравнивая выражения для условной плотности и условного распределения (см. замечание Л8.Р1.З3).
| 3) | +∞ ∫ -∞ | fx(x|y) dx = 1 по свойствам 2)f(x|y), 4)F(x|y). |
4)
| fX(x | y) = | ∂FX(x|y) ∂x | , |
если плотности f(x,y), fY(y) непрерывны. Действительно, по замечанию Л8.Р1.З3 имеем
| fx( x | y) | Δ = | ∂Fx( x | y) ∂x | = | 1 fY(y) | ∂ ∂x | x ∫ -∞ | f(x,y) dx = | f(x,y) fY(y) | . |
5) Если непрерывные СВ X и Y независимы, то fX(x|y) = fX(x). Согласно свойству 8)f(x,y) для независимых СВ X и Y имеем равенство f(x,y) = fX(x)fY(y), из которого следует по определению условной плотности, что fX(x|y) = fX(x).
6)
| P{x1 ≤ X ≤ x2} = | ∞ ∫ -∞ | fY(y) ( | x2 ∫ x1 | fX(x|y) dx ) dy. |
Действительно, по свойствам 3)f(x), 6)f(x,y) и определению условной плотности имеем
| P{x1 ≤ X ≤ x2} = | x2 ∫ x1 | fX(x) dx = | x2 ∫ x1 | ( | ∞ ∫ -∞ | f(x,y) dy ) dx = |
| = | x2 ∫ x1 | ( | ∞ ∫ -∞ | fY(y)fX(x|y) dy ) dx = | ∞ ∫ -∞ | fY(y) ( | x2 ∫ x1 | fX(x|y) dx ) dy. |
Условные числовые характеристики
Условным математическим ожиданием является выражение:
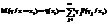 ;
; 
Условной дисперсией называется выражение:
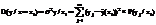 ;
;
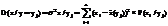 .
.
Корреляционные зависимости
Ковариацией (корреляционным моментом) kXY непрерывных СВ X и Y называется второй центральный смешанный момент
| kXY | Δ = | M[(X - mX)(Y - mY)] = | +∞ ∫ -∞ | +∞ ∫ -∞ | (x - mX)(y - mY)f(x,y) dx dy . |
Ковариация нормированных СВ
| * X и | * Y |
называется коэффициентом корреляции, т.е.
| rXY | Δ = | k | * * XY | Δ = | M[ | * * XY | ] | 2)mx = | M[(X - mX)(Y - mY)] σXσY | Δ = | kXY σXσY | . |
Определение 3. СВ X и Y называют коррелированными, если rXY ≠ 0 (kXY ≠ 0) и некоррелированными, если rXY = 0 (kXY = 0).
Определение 4. Корреляция между СВ X и Y называется положительной, если rXY > 0 и отрицательной, если rXY < 0.
Нормальный закон распределения случайной двумерной величины.