Основные дискретные распределения.

Вырожденное распределение.

Говорят, что случайная величина X имеет вырожденное распределение, если она принимает единственное значение с вероятностью 1. Обозначим такую случайную величину W_a, где a - значение, принимаемое этой случайной величиной, так что

P ( W _a = a ) = 1.

Испытание Бернулли.

Определение 1. Биномиальное распределение Bi(1, p) с параметрами n = 1 и p О [0,1] называется распределением Бернулли.

Замечание 1. Для распределения Bi(1, p) имеем по замечанию 2 из предыдущего раздела g(t) = q + pe^it, m_x = p, d_x = p(1-p).

Замечание 2. Распределение Бернулли Bi(1, p) играет фундаментальную роль в теории вероятностей и математической статистике, являясь математической моделью опыта с двумя исходами (см. замечание Л10.Р2.З6).

Замечание 3. Если X_m, m = 1,n, - независимые СВ (см. понятие Л9.Р1.О5) с распределением Bi(1, p), тогда СВ

X

Δ =

n ∑ m=1

Xm

имеет распределение Bi(n, p).

Пример 1. Пусть имеется партия некоторого товара, в котором товар с дефектами встречается с вероятностью 1 - p, а товар без дефектов - с вероятностью p. Положим x₀ = 1, если попался товар без дефектов, и x₁ = 0, если товар с дефектом. Тогда "качество" товара можно описать случайной величиной, имеющей распределение Бернулли Bi(1, p).

Биноминальное распределение.

n испытаний называются системой испытаний Бернулли, если испытания независимы, в каждом из них происходит событие 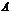, либо 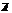с вероятностью наступления P(A) = p;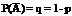

Найдем вероятность того, что в результате проведенных n испытаний событие А произошло m раз:

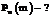
Рассмотрим композицию n независимых испытаний и построим композиционное пространство элементарных событий.

Общий вид элемента этого пространства следующий:

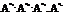
где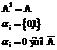

При этом вероятность наступления такого события равна:

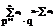(умножение при независимых событиях)

Найдем вероятность наступления любого элементарного события из композиционного пространства:

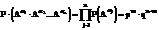
Рассмотрим в композиционном вероятностном пространстве событие: в n испытаниях событие A произошло m раз.

Событие A состоит из 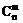- общее кол-во элементарных событий, в которое входит событие А. А произошло m раз, 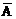- n-m раз. Вероятность каждого из этих элементарных событий одинакова и равна:

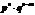
Следовательно, на основании III аксиомы теории вероятности результат равняется:

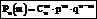(сложение вероятностей)

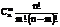
Распределение Пуассона.

Определение 1. Дискретная СВ X с реализациями x_k = k, k = 0,1,... имеет распределение Пуассона с параметром a > 0, что символически записывается как X ~ П(a), если

pk

Δ =

P{X = xk } =

ak k!

e-a.

Замечание 1. Найдём Характеристическую функцию СВ X ~ П(а):

g(t)

Δ =

∞ ∑ k=0

pkeitk =

∞ ∑ k=0

ak k!

e-aeitk =

= e-a

∞ ∑ k=0

(aeit)k k!

= e-aeae

it

= ea(e

it

-1) .

По свойству 3)g(t) получаем математическое ожидание и дисперсию

mx

Δ =

ν1 =

1 i

d dt

g(t)

|

t =0

=

1 i

[a i eitea(e

it

-1)]

|

t =0

= a ;

ν2 =

1 i2

d2 dt2

g(t)

|

t =0

=

a i

[i eitea(e

it

-1)]

|

t =0

= a(1+a) ;

d_x = ν₂-m_x² = a.

Замечание 2. Для распределения Пуассона характерно числовое равенство m_x = d_x = a, но при этом физические размерности m_x и d_x не совпадают.

Замечание 3. Распределение Пуассона широко используется в теории массового обслуживания. Приведем пример типичной ситуации, когда возникает такое распределение.

Пример 1. Пусть на телеграфную станцию в произвольные моменты времени случайным образом поступают заявки на переговоры с городом N так, что выполняются два условия:
а) вероятность появления любого количества заявок за какой-либо отрезок времени не зависит от того, сколько их поступило за любой другой, не пересекающийся с ним отрезок, т.е. заявки распределяются на оси времени t независимо друг от друга. Это условие независимости;
б) вероятность появления за достаточно малый интервал времени длины Δt двух и более заявок пренебрежимо мала по сравнению с вероятностью поступления в течении этого интервала времени не более одной заявки, которая пропорциональна Δt с коэффициентом пропорциональности a. Это условие ординарности.
В данном случае можно показать, что СВ X, равная числу заявок, поступивших на телефонную станцию за единицу времени имеет распределение П(a), где a - среднее число заявок, поступающих в единицу времени.

Пример 2. Пусть машина проехала Δ километров и X - число проколов шины на этом расстоянии. Тогда вероятность k проколов шины может быть найдена по формуле Пуассона (с соответствующим параметром a).

Замечание 4. Между биномиальным распределением Bi(n, p) и распределением Пуассона П(a) имеется следующая связь

Теорема 1. (Пуассона) Пусть n → ∞, p → 0 и при этом np ≡ a = const. Тогда

Pn(k) →

ak k!

e-a ,

где Pn(k)

Δ =

Cnkpkqn-k , k = 0,n .

Замечание 5. Докажем это утверждение, пользуясь замечательным пределом (1 - a/n)ⁿ → e^-a при n → ∞. Так как здесь p = a/n, q = 1 - a/n, то по определению Л5.Р1.О1 получаем

l i m n → ∞

Pn(k) =

l i m n→∞

n(n-1)...(n-k+1) k!

(a/n)k(1-a/n)n-k =

=

ak k!

l i m n→∞

n(n-1)...(n-k+1) nk

(1-a/n)n (1-a/n)k

=

ak k!

e-a.

Замечание 6. Таким образом, при больших n и малых p (при редких явлениях) выполняется закон малых чисел, в соответствии с которым сложное двухпараметрическое биномиальное распределение Bi(n, p) можно приближенно заменить однопараметрическим распределением Пуассона П(а), где а = nр. При этом ошибка от такой замены не превышает np², т.е.

|Cnkpkqn-k -

(np)k k!

e-np | ≤ np2.

Если условия теоремы Пуассона не выполняются, т.е. p достаточно велико, то существует другая оценка P_n(k) (см. теорему Муавра-Лапласа Л11.Р2.З3), которая основана на законе больших чисел.

Пример 3. Пусть некоторая система содержит 5000 независимо работающих элементов. Вероятность отказа каждого равна 0.001. Найдем вероятность отказа системы, если известно, что он происходит при отказе двух и более ее элементов. Число отказавших элементов является СВ X ~ Bi(5000,0.001). Поскольку значение n = 5000 велико, p = 0.001 мало (а = np = 5) и, кроме того, np² = 0.005 - приемлемая точность, то воспользуемся замечанием 4:

P{X ≥ 2} = 1 - P{X ≤ 1} = 1 - P₅₀₀₀(0) - P₅₀₀₀(1) ≈ 0.9596.

Теорема Пуассона.

Если число испытаний n в схеме независимых испытаний Бернулли стремится к бесконечности и 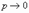так, что 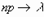, , 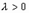то при любых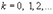

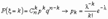
Это означает, что при больших n и малых p вместо громоздких вычислений по точной формуле 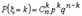можно воспользоваться приближенной формулой

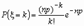, т.е. использовать формулу Пуассона для l = np.

На практике пуассоновским приближением пользуются при npq < 9.