Закон больших чисел. Теорема Бернулли.

Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. Закон больших чисел состоит из нескольких теорем, в которых доказывается приближение средних характеристик при соблюдении определённых условий к некоторым постоянным значениям.

Теорема Бернулли устанавливает связь между относительной частотой появления события и его вероятностью.

При достаточно большом числе независимых испытаний 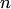с вероятностью, близкой к единице, можно утверждать, что разность между относительной частой появления события 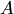в этих испытаниях е го вероятностью в отдельном испытании по абсолютной величине окажется меньше сколь угодно малого числа 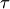, если вероятность наступления этого события в каждом испытании постоянна и равна р.

Утверждение теоремы Бернулли можно записать в виде неравенства

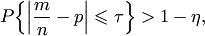где 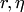— любые сколь угодно малые положительные числа.
Используя свойства математического ожидания и дисперсии, а также неравенство Чебышева, формулу можно записать в виде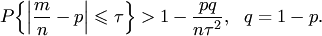

При решение практических задач иногда бывает необходимо оценить вероятность наибольшего отклонения частоты появлений события от её ожидаемого значения. В этом случае случайной величиной является число появления события 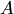в 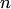независимых испытаниях. Имеем

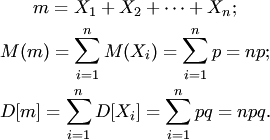
Используя неравенство Чебышева, получаем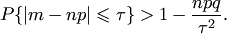

Центральная предельная теорема. Различные формулировки.

Математическая статистика как наука. Основные понятия. Задачи математической статистики.

Математическая статистика – раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей. Предметом математической статистики является изучение случайных величин (или случайных событий, процессов) по результатам наблюдений. Совокупность всех подлежащих изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях

над одним объектом, называется генеральной совокупностью.

Выборочной совокупностью (выборкой) называют совокупность объектов, отобранных случайным образом из генеральной совокупности. Более строго: выборка – это последовательность X1, X2, … Xn независимых одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением генеральной случайной величины.

Число объектов (наблюдений) в совокупности, генеральной или выборочной, называется ее объемом; обозначается соответственно через N и n.

Конкретные значения выборки, полученные в результате наблюдений (испытаний), называют реализацией выборки и обозначают строчными буквами x1, х2 …хn.

Метод статистического исследования, состоящий в том, что на основе изучения выборочной совокупности делается заключение о всей генеральной совокупности, называется выборочным.

Различают выборки с возвращением (повторные) и без возвращения (бесповторные). В первом случае отобранный объект возвращается в генеральную совокупность перед извлечением следующего; во втором – не возвращается. На практике чаще используется бесповторная выборка.

Выделим основные задачи математической статистики:

1. Задача определения закона распределения случайной величины (или системы случайных величин) по статистическим данным

2. Задача проверки правдоподобия гипотез

3. Задача нахождения неизвестных параметров распределения