Мгновенный центр ускорений (МЦУ)
В учебной литературе доказывается, что при движении фигуры в плоскости в каждый момент времени существует такая точка плоской фигуры, ускорениекоторой в этот момент равно нолю.
Эту точку называют мгновенным центром ускорений (МЦУ). В наших рассуждениях будем обозначать ее буквой Q. Взяв эту точку за полюс, получим формулу для определения ускорения произвольной точки:
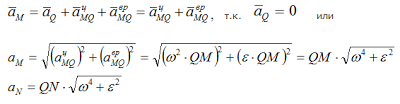
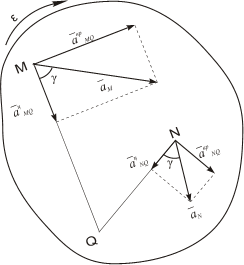
Рис. 1.12
Угол, который составляет вектор ускорения точки М с линией MQ определится из соотношения:
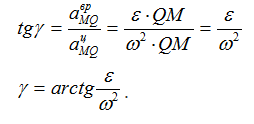
Т.е. у всех точек плоской фигуры этот угол одинаков. Из рис. 1.12 видно, что мгновенный центр ускорений лежит в точке пересечения линий, составляющих угол γ с соответствующими ускорениями точек.
На рис. 1.13-1.15 приведены частные случаи определения положения мгновенного центра ускорений.
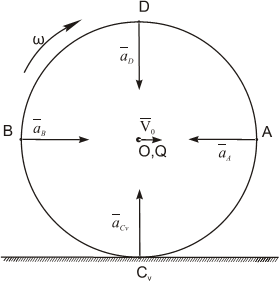
Рис. 1.13а

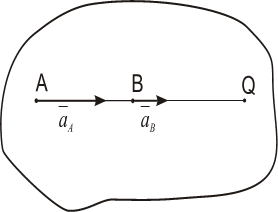
Рис. 1.13б
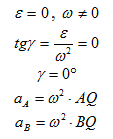
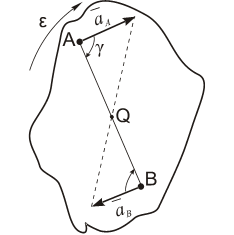
Рис. 1.14а
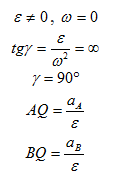
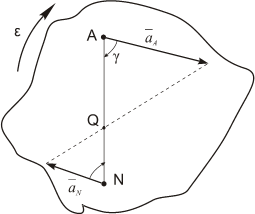
Рис. 1.14б
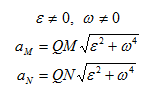
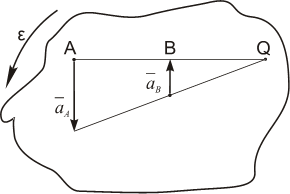
Рис. 1.15а
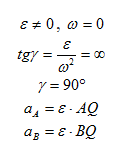
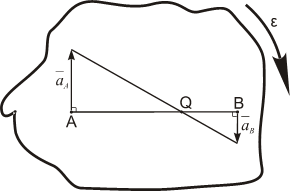
Рис. 1.15б
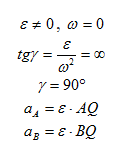
Информация по угловой скорости http://www.teoretmeh.ru/ukazankinematika3.htm
Сложное движение точки. Абсолютное, относительное и переносное движение точки. Связь между производными вектора в двух пространствах. Теоремы сложения скоростей и ускорений точки. Нахождение ускорения Кориолиса.
Теория сложного движения точки
Основные понятия и определения
При решении многих инженерных задач приходится рассматривать движение точки по отношению к некоторому твердому телу, которое в свою очередь движется.
При математическом описании такого сложного движения вводится неподвижная система отсчета и система отсчета жестко связанная с движущимся твердым телом, т.е. подвижная система отсчета. Тогда движение точки относительно подвижной системы отсчета называется относительным движением.
Движение твердого тела и неизменно связанной с ним подвижной системы отсчета относительно неподвижной системы называется переносным движением, а движение точки относительно неподвижной системы – абсолютным движением.
Соответственно вводятся понятия абсолютной скорости и абсолютного ускорения Va, aa, относительной скорости и относительного ускорения Vr, ar. Понятия переносной скорости и переносного ускорения Ve, ae требуют уточнения.
Переносной скоростью и переносным ускорением называется скорость и ускорение той точки твердого тела или подвижной системы отсчета, в которой в данный момент находится движущаяся точка.
Пример сложного движения
Рассмотрим пример, показанный на рис. 1. Диск вращается вокруг оси, проходящей через центр диска перпендикулярно к его плоскости, с угловой скоростью ω. Введем подвижную систему отсчета xOy, которая вращается вместе с диском.
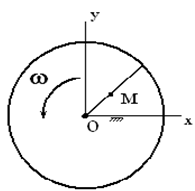
Рис. 1
По радиусу диска движется точка M по закону OM = s(t).
Таким образом, точка M участвует в двух движениях. Движется относительно диска по радиусу (относительное движение) и, вместе с диском, вращается вокруг оси, проходящей через центр диска (переносное движение).
Относительной скоростью и относительным ускорением точки M будет являться скорость и ускорение в движении вдоль радиуса диска. Переносной скоростью и переносным ускорением будет являться скорость и ускорение той точки диска, в которой в данный момент находится точка M.
