Программа 11. Сумма положительных чисел

В программе в бесконечном цикле for вводятся и суммируются положительные числа, отрицательные числа игнорируются, а при поступлении нуля используется break для выхода из цикла.

// Файл SumPos.cpp

// Подсчет суммы положительных чисел и их количества

#include <iostream.h>

#include <conio.h>

int main()

{

int x, sum = 0; // Вводимое число и сумма

int i; // Параметр цикла

int ipos = 0; // Количество введенных положительных чисел

cout << "\nВводите числа:\n";

for(i = 0; ; i++){ // Бесконечный цикл

cin >> x;

if(x < 0) // Если число отрицательное,

continue; // переход к повторению цикла

if(x == 0)

break; // Выход из цикла

sum += x; // Увеличение суммы

ipos++; // Увеличение счетчика положительных чисел

}

cout << "Введено " << i << ” чисел, \n”;

cout << ” из них ” << ipos << ” положительных \n";

cout << "Сумма положительных sum = " << sum << "\n";

getch();

return 0;

}

Результаты работы программы:

Вводите числа:

1 2 3 -1 -4 6 7 -3 -9 0

Введено 9 чисел,

из них 5 положительных

Сумма положительных sum = 19

Задачи 18-52. Выбор и циклы

18. Напишите программу, которая вводит целое число и проверяет, является оно четным или нечетным.

19. Напишите программу, вводящую три числа и печатающую наибольшее из них.

20. Дано трехзначное целое число. Требуется проверить, делится ли оно на 3. Известно, что число делится на 3, если на 3 делится сумма его цифр.

21. Дано трехзначное целое число. Проверить, читается ли оно одинаково слева направо и справа налево. Такие числа называются палиндромами.

22. Напишите программу, которая запрашивает номер месяца и выводит соответствующее название времени года.

23. Напишите программу, которая спрашивает Ваш возраст в годах и выводит его с правильным использованием слов «год» или «лет», например, 17 лет, 21 год, 22 года.

24. Напишите программу, вводящую номер месяца и выводящую его название.

25. В старояпонском календаре был принят 60–летний цикл, основанный на пяти 12–летних подциклах. Подциклы обозначались названиями цвета: зеленый, красный, желтый, белый и черный. Внутри каждого подцикла годы носили названия животных: крысы, коровы, тигра, зайца, дракона, змеи, лошади, овцы, обезьяны, курицы, собаки и свиньи. (1984 год – год зеленой крысы – был началом очередного цикла). Напишите программу, которая вводит номер некоторого года, больший чем 1984, и печатает его название по старояпонскому календарю.

26. Даны координаты вершин треугольника и координаты некоторой точки внутри него. Найти расстояние от данной точки до ближайшей стороны треугольника. (При определении расстояний учесть, что площадь треугольника можно вычислить и через три его вершины и через произведение площади основания на высоту.)

При решении следующих задач нужно применить наиболее подходящий из циклов while, for, do while.

27. Напишите программу, печатающую таблицу значений функции

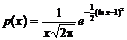
для x = 0.1, 0.2, ... , 2.

28. Напишите программу, печатающую таблицу умножения для чисел от 0 до 9 в десятичной системе счисления.

29. Дано целое k от 1 до 180. Определить, какая цифра находится в k-й позиции последовательности 10111213…99, в которой выписаны подряд все двузначные числа.

30. Дано натуральное k. Определить k-ю цифру последовательности 110100100010000100000…, в которой выписаны подряд степени 10.

31. Напишите программу, определяющую k – количество цифр в десятичной записи целого неотрицательного числа n.

32. Напишите программу, подсчитывающую количество двоичных цифр, требуемых для записи целого неотрицательного числа n

33. Числа Фибоначчи fn определяются формулами:

f₀ = f₁ = 1; f_n =f_n-1 + f_n-2 при n = 2, 3,…

Напишите программу, выводящую число Фибоначчи с заданным номером n > 1.

34. Напишите программу, печатающую таблицу чисел Фибоначчи, номера которых не превышают заданного значения n.

35. Напишите программу, выводящую число Фибоначчи с заданным номером n > 1.

36. Напишите программу, выводящую все числа Фибоначчи, значения которых не превышают некоторого числа N.

37. Вычислить S – сумму всех чисел Фибоначчи, которые не превосходят 1000.

38. Напишите программу, вводящую заданное число n пар вещественных чисел x, y. Рассматривая эти пары как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь которого попадают все эти точки.

39. Дана непустая последовательность положительных вещественных чисел x₁, x₂, … , x_n (n заранее не известно), за которой следует отрицательное число. Вычислить величину

nx₁+ (n–1)x₂ + … + 2x_n-1 +x_n.

40. Дана последовательность целых чисел. Определить количество чисел в наиболее длинной подпоследовательности из подряд идущих нулей.

41. Определить, является ли заданное натуральное число n совершенным, то есть равным сумме всех своих положительных делителей, кроме самого этого числа. Например, число 6 – совершенно: 6 = 1 + 2 + 3.

42. Дано целое n > 0. Напечатать все простые числа из диапазона [2, n]. Простым называется число, которое не имеет делителей, кроме 1 и самого себя.

43. Определить, является ли заданное натуральное число палиндромом, то есть таким, запись которого в десятичной системе счисления читается одинаково слева направо и справа налево.

44. Дано натуральное k. Определить k – ю цифру последовательности 12345678910111213 …, в которой выписаны подряд все натуральные числа.

45. Найти все целые корни уравнения

x³ + bx² + cx +d = 0,

где b, c, d – заданные целые числа, причем d ¹ 0.

Замечание. Целыми корнями могут быть только положительные и отрицательные делители коэффициента d.

46. Дано натуральное число n. Напечатать все числа от 1 до n в десятичной и двоичной системах счисления.

47. Напишите программу, вводящую положительные числа x₁, x₂,.. Признаком окончания ввода является ввод нуля или отрицательного числа. Вычислить y=x₁+x₁x₂+x₁x₂x₃+…+ x₁x₂ ××× x_m, где m – число введенных положительных чисел.

48. Подсчитать количество «счастливых» шестизначных автобусных билетов, то есть таких, в номерах которых сумма первых трех цифр равна сумме трех последних. (Можно воспользоваться тем, что количество «счастливых» билетов равно s₀²+s₁²+s₂²+…+s₂₇², где s_n, n = 0, 1,…, 27 – количество чисел от 0 до 999, сумма цифр которых равна n.)

49. Напишите программу, вычисляющую факториал заданного натурального числа n. Факториал n – это последовательное произведение всех чисел от 1 до n: n! = 1∙2∙3∙…∙(n-1) n.

50. Дано вещественное число x и вещественное число e>0. Вычислить с точностью e значение следующей функции

e^x=1 + x/1! + x²/2! + … + xⁿ/n! + …

Вычисления прекратить, когда очередной член суммы xⁿ/n! станет по модулю меньше e.

51. Вычислите с заданной точность e > 0 приближенное значение синуса, используя ряд:

sin x = x - x³/3! + x⁵/5! -…+(-1)ⁿx²ⁿ⁺¹/(2n+1)!+…

52. Не используя стандартные функции, за исключением abs, вычислить с заданной точностью eps>0

y=arctg x = x – x³/3 + x⁵/5 + … + (-1)ⁿx²ⁿ⁺¹/(2n+1) + … (|x| < 1).

Глава 6. Массивы

Массив представляет собой набор последовательно пронумерованных элементов одного типа. Все элементы массива имеют одно имя, но каждый элемент имеет свой номер, с помощью которого отличается от других элементов.

Нумерация элементов массива начинается с нуля.

В памяти элементы массива располагаются подряд, один за другим.

Одномерные массивы

При объявлении массива после его имени в квадратных скобках указывается количество элементов, например,

double x[100];

Здесь x – это имя массива из 100 элементов типа double.

При обращение к элементу массива его номер указывается в квадратных скобках.

Так как нумерация элементов массива начинается с нуля, то x[0] есть первый элемент массива, x[99] – последний. Не существует элемента x[100], в том смысле, что под него не выделяется память, хотя после 99-го элемента память не заканчивается и к ней можно обратиться посредством выражения x[100]. Поскольку этот участок памяти не числится за массивом x, он может использоваться для других целей или программой, или операционной системой, поэтому обращение к нему, особенно запись в него какого-то значения, может привести к ошибочному, непредсказуемому поведению программы. В других языках, например, в Паскале, контролируется выход индекса за границы массива. В C++ такого контроля нет, сам программист должен следить за этим.

Массивы в языке C++ имеют всегда конкретную размерность, нельзя определять массивы переменной длины.

Массив может состоять из элементов любых типов.

Массив можно инициализировать при его определении, указав в фигурных скобках список значений элементов. Например, массив с количеством дней в каждом месяце можно инициализировать так:

int days[] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

Если размер массива не указан, то длину массива вычисляет компилятор по списку инициализации. Для приведенного примера это 12.

Если количество инициализаторов меньше заданного размера массива, оставшиеся элементы будут нулевыми. Пусть, например, определен массив:

int y[6] = {1, 2, 3};

У массива y элементы будут иметь следующие значения: y[0] = 1, y[1] = 2, y[2] = 3, y[3] = 0, y[4] = 0, y[5] = 0.

Задание слишком большого числа инициализаторов является ошибкой, например,

int z[3] = {1, 2, 3, 4, 5}; // Ошибка, слишком много инициализаторов

Оператор sizeof, примененный к массиву, дает размер массива в байтах. Например, для массива days выражение sizeof(days) / sizeof(int) равно 12, так как массив состоит из 12 элементов типа int. Здесь sizeof(days) – размер памяти в байтах, выделенной под массив, sizeof(int) – размер типа int в байтах.

Над массивами в целом нельзя выполнять какие-либо действия (присваивать, складывать и т.п.), можно работать только с отдельными элементами массива.