Поступательное движение твердого тела.

Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.

Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли и т.д.

Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.

Доказательство.

Если выбрать две точки твердого тела А и В , то радиусы-векторы этих точек связаны соотношением

Траектория точки А – это кривая, которая задается функцией r_A(t), а траектория точки B – это кривая, которая задается функцией r_B(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.

Продифференцируем по времени скорость и получим выражение a_B = a_A. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.

Вращательное движение твердого тела.

Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки. Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П₀ и П , одна из которых неподвижна, а другая жестко связана с телом.

φ=φ(t) – уравнение вращательного движения твердого тела.

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

Угловая скорость.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

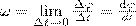
Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ . Размерность угловой скорости dim ω = Т^-1, а ее единица — радиан в секунду (рад/с).

Линейная скорость точки

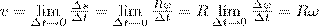
т.е

v=ωR

В векторном виде формулу для линейной скорости можно написать как векторное произведение:

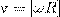
При этом модуль векторного произведения, по определению, равен ωRsin(ω, R), а направление совпадает с направлением поступательного движения правого винта его вращения от ω к R.

Если ω=const, то вращение равномерное и его можно характеризовать периодом вращения Т - временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2π. Так как промежутку времени Δt=Т соответствует Δφ=2π, то ω=2π/T, откуда

Т = 2π/ω.

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

n= 1/T = ω/(2π),

откуда

ω = 2πn.

Угловое ускорение.

Угловым ускорением называется векторная величина, равная первой производной yгловой скорости по времени:

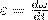
При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω , при замедленном - противонаправлен ему.

Тангенциальная составляющая ускорения a_τ=dv/dt , v = ωR и

Нормальная составляющая ускорения

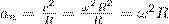
Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а_τ, нормальное ускорение а_n) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами:

s = Rφ, v = Rω, а_τ = R?, a_n = ω²R.

В случае равнопеременного движения точки по окружности (ω=const)

ω = ω₀ ± ?t, φ = ω₀t ± ?t²/2,

где ω₀ — начальная угловая скорость.