Корреляционное отношение и индекс корреляции

Введенный выше коэффициент корреляции, как уже отмечено, является полноценным показателем тесноты связи лишь в случае линейной зависимости между переменными. Однако часто возникает необходимость в достоверном показателе интенсивности связи при любой форме зависимости.

Для получения такого показателя вспомним правило сложения дисперсий:

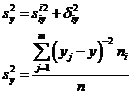(53, 54)

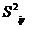— средняя групповых дисперсий 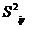, или остаточная диспепсия —

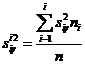
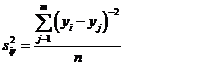
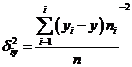(55, 56, 57) межгрупповая дисперсия

Остаточной дисперсией измеряют ту часть колеблемости Y, которая возникает из-за изменчивости неучтенных факторов, не зависящих от X. Межгрупповая дисперсия выражает ту часть вариации У, которая обусловлена изменчивостью X. Величина

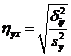(58)

получила название эмпирического корреляционного отношения У по X. Чем теснее связь, тем большее влияние на вариацию переменной доказывает изменчивость X.по сравнению с неучтенными факторами, тем выше n_ух. Величина n_ух. , называемая эмпирическим коэффициентом детерминации, показывает, какая часть общей вариацииУ обусловлена вариацией X. Аналогично вводится эмпирическое корреляционное отношение X по У:

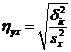(59)

Отметим основные свойства корреляционных отношений(при достаточно большом объеме выборки п):

1.Корреляционное отношение есть неотрицательная величина, не превосходящая 1: 0< η < 1.

2. Если η = 0, то корреляционная связь отсутствует. Если η = 1, то между переменными существует функциональная зависимость.

3. η _ух≠ η _ху, т.е. в отличие от коэффициента корреляции r(для которого r_ху= r_ух = r) при вычислении корреляционного отношения существенно, какую переменную считать независимой, а какую — зависимой.

Эти свойства справедливы как для эмпирических корреляционных отношений n, так и для теоретических — R .

Эмпирическое корреляционное отношение η _ух является показателем рассеяния точек корреляционного поля относительно эмпирической линии регрессии, выражаемой ломаной, соединяющей значения 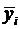. Однако в связи с тем, что закономерное изменение 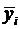нарушается случайными зигзагами ломаной, возникающими вследствие остаточного действия неучтенных факторов, η _ух преувеличивает тесноту связи. Поэтому наряду с η _ух.рассматривается показатель тесноты связи R_ух, характеризующий рассеяние точек корреляционного поля относительно линии регрессии у_х (12.3). Показатель R_ух получил название теоретического корреляционного отношения или индекса корреляции Y по X.

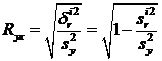(60)

где дисперси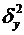и и 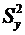определяются по формулам (54) —(56), в которых групповые средние 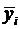, заменены условными средними 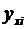, вычисленными по уравнению регрессии (16). Подобно R_ух вводится и индекс корреляции X по Y

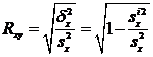(61)

Достоинством рассмотренных показателей η и R является то, что они могут быть вычислены при любой форме связи между переменными. Хотя η и завышает тесноту связи по сравнению с R, но для его вычисления не нужно знать уравнение регрессии. Корреляционные отношения η и R связаны с коэффициентом корреляции rследующим образом:

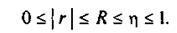(62)

Можно показать, что в случае линейной модели (3), т.е. зависимости, y_x- 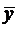=b_yx(x- 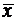) индекс корреляции R_ух равен коэффициенту корреляции r (по абсолютной ветчине): R_yx = | r |

.

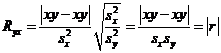Коэффициент детерминации R², равный квадрату индекса корреляции (для парной линейной модели — r²), показывает долю общей вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющей переменной. Чем ближе R² к 1, тем теснее наблюдения примыкают к линии регрессии, тем лучше регрессия описывает зависимость переменных.

Расхождение между η² и R² (или r²) может быть использовано для проверки линейности корреляционной зависимости.

Проверка значимости корреляционного отношения η основана на том, что статистика

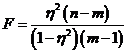(63)

(где m — число интервалов по группировочному признаку) имеет F-распределение Фишера—Снедекора с k₁=m — 1 и k₂=n — m степенями свободы. Поэтому η значимо отличается от нуля, если F >F_{α,, k1, k2}, где F_{α,, k1, k2}— табличное значение F-критерия на уровне значимости α при числе степеней свободы k₁ и k₂.

Индекс корреляции R двух переменных значим, если значение статистики

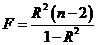(64)

больше табличного F_{α,, k1, k2}, где к₁ = 1 и к.₂ = п — 2.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Идея МНК основана на том, чтобы минимизировать сумму квадратов отклонений расчетных значений от эмпирических, т.е. нужно оценить параметры о функции f(a,x) таким образом, чтобы ошибки еi= уi-f(а,х), точнее - их квадраты, по совокупности были минимальными. Для этого нужно решить задачу минимизации суммы квадратов остатков S=e12+..+en2

Достоинства:

1. Наиболее простой метод выбора значений b₁ и b₂, чтобы остатки были минимальными;

2. При выполнении условий Гаусса-Маркова МНК-оценки будут наилучшими (наиболее эффективными) линейными (комбинации Y_i) несмещёнными оценками параметров регрессии (b₁ и b₂₎.

Условия Гаусса-Маркова:

- модель линейна по параметрам и правильно специфицирована;

- объясняющая переменная в выборке имеет некоторую вариацию;

- математическое ожидание случайного члена равно нулю;

- случайный член гомоскедастичен;

- значения случайного члена имеют взаимно независимые распределения;

- случайный член имеет нормальное распределение

Недостатки: МНК-оценки являются эффективными линейными несмещёнными ТОЛЬКО при выполнении ВСЕХ условий Гаусса-Маркова, что на практике встречается редко.