Равновесие системы тел. Статически определимые и статически неопределимые системы. Равновесие при наличии сил трения. Трение скольжения при покое и при движении.

Статический расчет системы тел сводится к рассмотрению условий равновесия конструкций, состоящих из тел, соединенных какими-нибудь связями. Связи, соединяющие части конструкции называются внутренними, скрепляющие конструкцию с другими телами, в нее не входящими - внешними.

При решении задач статики реакции связей входят в число неизвестных, которые необходимо определить из уравнений равновесия. Система тел, для которых число неизвестныхреакций связей равно числу уравнений равновесия, называются статически определимыми. Система тел, для которых число неизвестных реакций связей больше числа уравнений равновесия, называются статически неопределимыми.

Если при отбрасывании внешних связей (опор) конструкция остается жесткой, то для нее задача о равновесии решается как для абсолютно твердого тела (при действии плоской системы сил число неизвестных реакций связей не должно быть больше трех).

Если после отбрасывания внешних связей конструкция не считается жесткой, то наиболее рациональным способом решения подобных задач является расчленение на отдельные тела и составление уравнений равновесия для каждого из тел в отдельности.

Для конструкции из n тел, на каждое из которых действует произвольная плоская система сил, получится таким путем 3n уравнений равновесия, позволяющих найти 3n неизвестных.

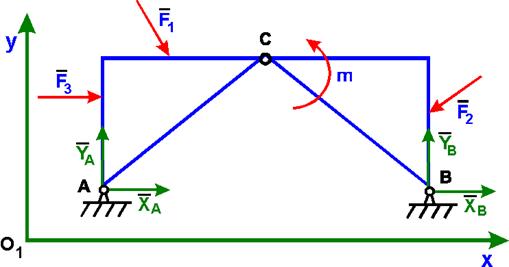
Например, если отбросить опоры А и В трехшарнирной арки, то она не будет жесткой: ее части могут поворачиваться вокруг шарнира С. Для определения реакций внешних связей Х_А, Y_А, Х_В,Y_В расчленим конструкцию по соединительному шарниру С на две части и рассмотрим равновесие каждой из частей в отдельности.

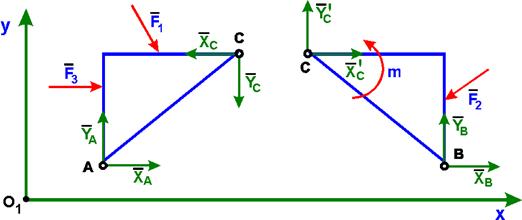
При действии на трех шарнирную арку произвольной плоской системы сил для каждой части можно записать три уравнений равновесия:

для АС для СВ

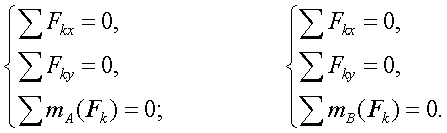
Присоединить к этой системе шести уравнений на основании закона о действии и противодействии уравнения для узла С (Х_С = Х_С, Y_С = Y_С), получим систему уравнений из которой можно найти реакции внешних связей Х_А, Y_А, Х_В, Y_В и реакции внутренних связей Х_С, Y_С.

Если при рассмотрении заданной системы, находящейся в рав­новесном состоянии от действия заданных внешних нагрузок, все реакции в связях закрепления, а также внутренние усилия в ее эле­ментах, можно определить только по методу сечений, без использо­вания дополнительных условий, то такая система называется ста­тически определимой.

В реальной практике встречаются такие конструкции при рас­чете которых одних лишь уравнений равновесия оказывается не­достаточно, в связи с чем требуется формулирование дополнитель­ных уравнений, связанных с условиями деформирования конструк­ции.

Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.